- Research Article
- Open access
- Published:
Analytic Classes on Subframe and Expanded Disk and the 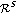 Differential Operator in Polydisk
Differential Operator in Polydisk
Journal of Inequalities and Applications volume 2009, Article number: 353801 (2009)
Abstract
We introduce and study new analytic classes on subframe and expanded disk and give complete description of their traces on the unit disk. Sharp embedding theorems and various new estimates concerning differential  operator in polydisk also will be presented. Practically all our results were known or obvious in the unit disk.
operator in polydisk also will be presented. Practically all our results were known or obvious in the unit disk.
1. Introduction and Main Definitions
Let  and
and  be the
be the  -dimensional space of complex coordinates. We denote the unit polydisk by
-dimensional space of complex coordinates. We denote the unit polydisk by

and the distinguished boundary of  by
by

We use  to denote the volume measure on
to denote the volume measure on  and
and  to denote the normalized Lebesgue measure on
to denote the normalized Lebesgue measure on  Let
Let  be the space of all holomorphic functions on
be the space of all holomorphic functions on  When
When  we simply denote
we simply denote  by
by 
 by
by 
 by
by 
 by
by  We refer to [1, 2] for further details. We denote the expanded disk by
We refer to [1, 2] for further details. We denote the expanded disk by

and the subframe by

The Hardy spaces, denoted by  are defined by
are defined by

where 

For  recall that the weighted Bergman space
recall that the weighted Bergman space  consists of all holomorphic functions on the polydisk satisfying the condition
consists of all holomorphic functions on the polydisk satisfying the condition

For  the Bergman class on expanded disk is defined by
the Bergman class on expanded disk is defined by

and similarly the Bergman class on subframe denoted by  is defined by
is defined by

where 
Throughout the paper, we write  (sometimes with indexes) to denote a positive constant which might be different at each occurrence (even in a chain of inequalities) but is independent of the functions or variables being discussed.
(sometimes with indexes) to denote a positive constant which might be different at each occurrence (even in a chain of inequalities) but is independent of the functions or variables being discussed.
The notation  means that there is a positive constant
means that there is a positive constant  such that
such that  We will write for two expressions
We will write for two expressions  if there is a positive constant
if there is a positive constant  such that
such that 
This paper is organized as follows. In first section we collect preliminary assertions. In the second section we present several new results connected with so-called operator of diagonal map in polydisk. Namely, we define two new maps  and
and  from subframe
from subframe  and expanded disk
and expanded disk  to unit disk
to unit disk  and, in particular, completely describe traces of Bergman classes
and, in particular, completely describe traces of Bergman classes  and
and  defined on subframe and expanded disk on usual unit disk
defined on subframe and expanded disk on usual unit disk  on the complex plane. Proofs are based among other things on new projection theorems for these classes.
on the complex plane. Proofs are based among other things on new projection theorems for these classes.
A separate section will be devoted to the study of  differential operator in polydisk. It is based in particular on results from the recent paper [3]. We will use the dyadic decomposition technique to explore connections between analytic classes on subframe, polydisk, and expanded disk. We also prove new sharp embedding theorems for classes on subframe and expanded disk. Last assertions of the final section generalize some one-dimensional known results to polydisk and to the case of
differential operator in polydisk. It is based in particular on results from the recent paper [3]. We will use the dyadic decomposition technique to explore connections between analytic classes on subframe, polydisk, and expanded disk. We also prove new sharp embedding theorems for classes on subframe and expanded disk. Last assertions of the final section generalize some one-dimensional known results to polydisk and to the case of  operators simultaneously.
operators simultaneously.
2. Preliminaries
We need the following assertions.
Lemma 2 A (see [4]).
Let  be a fixed
be a fixed  -tuple of nonnegative numbers and let
-tuple of nonnegative numbers and let  be an arbitrary family of
be an arbitrary family of  -boxes in
-boxes in  lying in the cube
lying in the cube  There exists a set
There exists a set  such that
such that  and for all
and for all  there exists
there exists  such that
such that 
The following proposition is heavily based on ideas from [4].
Proposition 2.1.

Let  be a nonnegative summable function on
be a nonnegative summable function on  Let
Let  Let
Let  where
where  and where
and where  is a family of all
is a family of all  boxes such that
boxes such that  is proportional to
is proportional to  for some fixed
for some fixed  Then the following statements hold:
Then the following statements hold:

where  and
and  are any positive Borel measures on
are any positive Borel measures on  and
and  such that
such that

where  (b) Let
(b) Let 

 Then
Then

Proof.
Proofs of all parts are similar. The first part of the lemma connected with  measure and unit disk can be found in [4]. We will give the complete proof of the second part. To prove the second part let
measure and unit disk can be found in [4]. We will give the complete proof of the second part. To prove the second part let 
Fix a point  in the
in the  and associate an
and associate an  - box
- box  such that
such that

We use standard covering Lemma A to construct a set  such that
such that  - boxes
- boxes  pairwise disjoint, we have
pairwise disjoint, we have

So the lemma will be proved if  Let
Let

Let  then we will show
then we will show 
 So
So  where
where  , and constant
, and constant  will be specified later. Hence we will have
will be specified later. Hence we will have 
The last estimate follows from inclusion 

It remains to show the inclusion  To show this inclusion we note if
To show this inclusion we note if  then we have
then we have  Using covering Lemma A we have
Using covering Lemma A we have  Hence
Hence

It remains to note that we put above 
-
(b)
Note that for the case of
 we can step by step repeat the same procedure with
we can step by step repeat the same procedure with  instead of
instead of  and the condition on
and the condition on 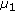 will be replaced by weaker condition
will be replaced by weaker condition 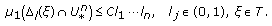 (29)
(29)
Note for 

Now part (b) can be obtained by direct calculation.
Remark 2.2.
In Proposition 2.1(b)  can be replaced by
can be replaced by 
Lemma 2.3.
Let  Then
Then

Estimate (2.11) for  can be found in [5] and in [1] for general case. The following lemma is well known.
can be found in [5] and in [1] for general case. The following lemma is well known.
Lemma 2.4.
Let  Then for
Then for  one has (a)
one has (a)  ; (b)
; (b)  ; (c)
; (c) 
Lemma 2.5 (see [3]).
Let 
 Then one has
Then one has

Corollary 2.6.
Let  Then
Then

We will need the following Theorems http://A and http://B.
Theorem 2 A (see [3]).

Let  Then
Then


Let  Then
Then

Theorem 2 B (see [3]).

Let  Then
Then


Let  Then
Then

3. Analytic Classes on Subframe and Expanded Disk
Let us remind the main definition.
Definition 3.1.
Let  be subspaces of
be subspaces of  and
and  We say that the diagonal of
We say that the diagonal of  coincides with
coincides with  if for any function
if for any function  , and the reverse is also true for every function
, and the reverse is also true for every function  from
from  there exists an expansion
there exists an expansion  such that
such that  Then we write
Then we write 
Note when  then
then

where  is an arbitrary analytic expansion of
is an arbitrary analytic expansion of  from diagonal of polydisk to polydisk.
from diagonal of polydisk to polydisk.
The problem of study of diagonal map and its applications for the first time was also suggested by Rudin in [2]. Later several papers appeared where complete solutions were given for classical holomorphic spaces such as Hardy, Bergman classes; see [1, 4, 6, 7] and references there. Recently the complete answer was given for so-called mixed norm spaces in [8]. Partially the goal of this paper is to add some new results in this direction. Theorems on diagonal map have numerous applications in the theory of holomorphic functions (see, e.g., [9, 10]).
In this section we concentrate on the study of two maps closely connected with diagonal mapping  from subframe into disk
from subframe into disk  where all
where all  and another map
and another map  from expanded disk into disk where
from expanded disk into disk where  and
and  function is from a functional class on subframe
function is from a functional class on subframe  or expanded disk
or expanded disk 
Note that the study of maps which are close to diagonal mapping was suggested by Rudin in [2] and previously in [11] Clark studied such a map.
Theorem 3.2.
Let  If
If
(a) or
or
(b) then for every function
then for every function  and for every function
and for every function  there exist
there exist  such that
such that 
Proof.
Note that one part of the theorem was proved in [3] and follows from Theorem A. Let us show the reverse. Let first  Consider the following
Consider the following  function:
function:

where  can be large enough,
can be large enough,  is a constant of Bergman from representation formula (see [1]), obviously
is a constant of Bergman from representation formula (see [1]), obviously  by Bergman representation formula in the unit disk. It remains to note that the following estimate hold by Lemma 2.3:
by Bergman representation formula in the unit disk. It remains to note that the following estimate hold by Lemma 2.3:

where  can be large enough. Using Fubini's theorem and calculating the inner integral we get what we need.
can be large enough. Using Fubini's theorem and calculating the inner integral we get what we need.
We consider now  case. Let
case. Let  Then
Then

by Bergman representation formula. Obviously  , as
, as

where  is a map from subframe
is a map from subframe  to diagonal. Using duality arguments and Fubini's theorem we have
to diagonal. Using duality arguments and Fubini's theorem we have

where 
We will need the following assertion. Let 
Then let

where  We assert that
We assert that  belongs to
belongs to 
Indeed using Hölder's inequality we get

where  We used above the estimate
We used above the estimate


Returning to estimate for  we have by Hölder's inequality
we have by Hölder's inequality

We used the fact that for all  proved before.
proved before.
The complete analogue of Theorem 3.2 is true for Bergman classes on expanded disk we defined previously.
Theorem 3.3.
Let  If
If
(a) or
or
(b) then the following assertion holds. For every function
then the following assertion holds. For every function  belongs to
belongs to  and the reverse is also true, for any function
and the reverse is also true, for any function  from
from  there exists a function
there exists a function  such that
such that  for all
for all 
Proof.
We give a short sketch of proof of Theorem 3.3 and omit details. Note that the half of the theorem the inclusion  was proved in [3] and follows directly from Theorem A.
was proved in [3] and follows directly from Theorem A.
For  we have to use again Lemma 2.3 and Fubini's theorem. For
we have to use again Lemma 2.3 and Fubini's theorem. For  we first prove
we first prove  if
if  and if
and if 

Indeed by Hölder's inequality we have

Hence calculating integrals we finally have 
We used the estimate

which is true under the conditions on indexes we have in formulation of theorem and can be obtained by using Hölder's inequality for  functions. Using this projection theorem and repeating arguments of proof of the previous theorem we will complete the proof of Theorem 3.3.
functions. Using this projection theorem and repeating arguments of proof of the previous theorem we will complete the proof of Theorem 3.3.
Remark 3.4.
Note that Theorems 3.2 and 3.3 are obvious for 
Remark 3.5.
Note that estimates between expanded disk, unit disk, and polydisk can be also obtained directly from Liuville's formula

Remark 3.6.
The complete description of traces of classes with  and
and  quasinorms on the unit disk can be obtained similarly by small modification of the proof of Theorem 3.2,
quasinorms on the unit disk can be obtained similarly by small modification of the proof of Theorem 3.2,

Let

We formulate complete analogues of Theorems 3.2 and 3.3 for classes 
Theorem 3.7.
Let  and
and  Then
Then  is in
is in  and any
and any  can be expanded to
can be expanded to  such that
such that  The same statement is true for pairs
The same statement is true for pairs 
Note that one part of statement is obvious. If, for example,  then
then  On the other side, let
On the other side, let  Then define as above that
Then define as above that


is big enough,  is a Bergman constant of Bergman representation formula.
is a Bergman constant of Bergman representation formula.
Obviously  Using Hölder's inequality for
Using Hölder's inequality for  functions we get
functions we get  Similarly
Similarly 
It is natural to question about discrete analogues of operators we considered previously.
Let  Let
Let

We have for such a function

As a consequence of these arguments and using Lemma 2.4 we have the following proposition, a discrete copy of assertions we proved above.
Proposition 3.8.
Let  and
and  Then
Then  if and only if
if and only if 


4. Sharp Embeddings for Analytic Spaces in Polydisk with 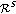 Operators and Inequalities Connecting Classes on Polydisk, Subframe, and Expanded Disk
Operators and Inequalities Connecting Classes on Polydisk, Subframe, and Expanded Disk
The goal of this section is to present various generalizations of well-known one-dimensional results providing at the same time new connections between standard classes of analytic functions with quazinorms on polydisk and  differential operator with corresponding classes on subframe and expanded disk.
differential operator with corresponding classes on subframe and expanded disk.
In this section we also study another two maps connected with the diagonal mapping from polydisk to subframe and expanded disk using, in particular, estimates for maximal functions from Lemma 2.3 which are of independent interest. Note that for the first time the study of such mappings which are close to diagonal mapping was suggested by Rudin in [2]. Later Clark studied such a map in [11].
In this section we also introduce the  differential operator as follows (see [3, 12, 13]).
differential operator as follows (see [3, 12, 13]).  where
where 
Note it is easy to check that  acts from
acts from  into
into 
In the case of the unit ball an analogue of  operator is a well-known radial derivative which is well studied. We note that in polydisk the following fractional derivative is well studied (see [1]):
operator is a well-known radial derivative which is well studied. We note that in polydisk the following fractional derivative is well studied (see [1]):

where 
 , and
, and  Apparently the
Apparently the  operator was studied in [12] for the first time. Then in [13], the second author studied some properties of this operator. In this section we also continue to study the
operator was studied in [12] for the first time. Then in [13], the second author studied some properties of this operator. In this section we also continue to study the  operator. We need the following simple but vital formula which can be checked by easy calculation:
operator. We need the following simple but vital formula which can be checked by easy calculation:

where  This simple integral representation of holomorphic
This simple integral representation of holomorphic  functions in polydisk will allow us to consider them in close connection with functional spaces on subframe
functions in polydisk will allow us to consider them in close connection with functional spaces on subframe 
The following dyadic decomposition of subframe and polydisk was introduced in [1] and will be also used by us:


averages in analytic spaces in polydisk can obviously have a mixed form, for example,  In [8] Ren and Shi described the diagonal of mixed norm spaces, but the above mentioned mixed case was omitted there. Our approach is also different. It is based on dyadic decomposition we introduced previously.
In [8] Ren and Shi described the diagonal of mixed norm spaces, but the above mentioned mixed case was omitted there. Our approach is also different. It is based on dyadic decomposition we introduced previously.
Theorem 4.1.
Let  and
and  Then
Then 
Proof.
Using diadic decomposition of polydisk we have

We used above the following estimate which can be found, for example, in [1]

where  are enlarged dyadic cubes (see [1]) and
are enlarged dyadic cubes (see [1]) and  , and
, and

Note further since 

We have

We used the fact that 
Hence using the fact that  is a finite covering of
is a finite covering of  finally we have for all
finally we have for all  One part of theorem is proved.
One part of theorem is proved.
To get the reverse statement we use the estimate from Lemma 2.3. Then we have

for any  Hence
Hence  and for
and for  by Lemma 2.3
by Lemma 2.3

Let  Then we may assume that again
Then we may assume that again  is large enough. Let
is large enough. Let  Then
Then

We used estimate

Choosing appropriate  we repeat now arguments that we presented for
we repeat now arguments that we presented for  above to get what we need. The proof is complete.
above to get what we need. The proof is complete.
Remark 4.2.
The case of  averages can be considered similarly. Note in Theorem 4.1
averages can be considered similarly. Note in Theorem 4.1 Thus our Theorem 4.1 extends known description of diagonal of classical Bergman classes (see [1, 7]).
Thus our Theorem 4.1 extends known description of diagonal of classical Bergman classes (see [1, 7]).
In [14] Carleson as Rudin and Clark showed that in the case of the polydisk one cannot expect so simple description of Carleson measures as one has for measures defined in the disk. We would like to study embeddings of the type

where  is a positive Borel measure on
is a positive Borel measure on  and
and  is a Bergman class on polydisk or subframe.
is a Bergman class on polydisk or subframe.
Theorem 4.3.
Let  , and
, and  is a positive Borel measure on
is a positive Borel measure on  If
If

then

and conversely if

holds for some  where
where  then
then

Remark 4.4.
With another  -sharp" embedding theorem, the complete analogue of Theorem 4.3 is true also when we replace the left side by
-sharp" embedding theorem, the complete analogue of Theorem 4.3 is true also when we replace the left side by  The proof needs small modification of arguments we present in the proof of Theorem 4.3.
The proof needs small modification of arguments we present in the proof of Theorem 4.3.
Remark 4.5.
For  and
and  Theorem 4.3 is known (see [15]).
Theorem 4.3 is known (see [15]).
Proof of Theorem 4.3.
It can be checked by direct calculations based on formula (4.2) that the following integral representation holds:


Using the fact that  in increasing by
in increasing by  and
and  (see [1]) we get from above by using the estimate
(see [1]) we get from above by using the estimate

where  is growing measurable,
is growing measurable, 

To obtain the reverse implication we use standard test function  and Lemma 2.5
and Lemma 2.5

where 
The rest is clear. The proof is complete.
Below we continue to study connections between standard classes in polydisk and corresponding spaces on subframe and expanded disk.
Let

Let us note that Theorems 3.2 and 3.7 of [3] show that under some restrictions on  the following assertion is true.
the following assertion is true.
For every function  belongs to
belongs to  and the reverse is also true, for any function
and the reverse is also true, for any function  there exists "an extension"
there exists "an extension"  such that
such that

The following Theorem 4.6 gives an answer for the same map from polydisk to expanded disk

for  functions from
functions from 
We will develop ideas from [4] to get the following sharp embedding theorem for classes on expanded disk.
Theorem 4.6.
Let  be a positive Borel measure on
be a positive Borel measure on  Then
Then

if and only if 
Proof.
Obviously if  then by putting
then by putting

we have  and
and 
 Hence we get what we need. Now we will show the sufficiency of the condition.
Hence we get what we need. Now we will show the sufficiency of the condition.
Let 
Let  Let also
Let also  and
and  where
where

In what follows we will use notations of Proposition 2.1. Consider the Poisson integral of a function  (see [2]).
(see [2]).
Let  We will show now as in [4] that
We will show now as in [4] that

Indeed, this will be enough, since the operator  is
is  operator we can apply the Marcinkiewicz interpolation theorem (see [16, Chapter 1]) to assert that
operator we can apply the Marcinkiewicz interpolation theorem (see [16, Chapter 1]) to assert that

We have as in [4] for 

where we used the standard partition of Poisson integral. Hence  and so using Proposition 2.1 we finally get
and so using Proposition 2.1 we finally get 
Indeed by Proposition 2.1 we have

Theorem 4.6 is proved.
Theorem 4.7.
Let  Then
Then

where 

where 

where 
Proof.
We use systematically the integral representation (4.18), Lemma 2.5, and it is corollary. The proof of the estimate (4.32) follows from equality


and estimate


obtained during the proof of Theorem 4.3.
The proof of the estimate (4.33) follows from Lemma 2.5 and its corollary and integral representation (4.35).
The proof of the estimate (4.34) follows from equality 

Indeed using (4.36) integrating both sides of (4.37) by  and using Lemma 2.5 we arrive at (4.34).
and using Lemma 2.5 we arrive at (4.34).
Remark 4.8.
All estimates in Theorem 4.7 for  are well known (see [1, Chapter1]).
are well known (see [1, Chapter1]).
We present below a complete analogue of Theorems 3.2 and 3.3 for a map from polydisk to expanded disk. Note the continuation of  function is done again from diagonal
function is done again from diagonal  Let
Let  and
and

where  is a constant of Bergman representation formula (see [1]).
is a constant of Bergman representation formula (see [1]).
Proposition 4.9.

Then

And reverse is also true:

Let  and
and

then for all functions  such that condition (4.38) holds for
such that condition (4.38) holds for  we have
we have 

Let  Then
Then

and the reverse is also true:

For any function  with a finite quasinorm
with a finite quasinorm  such that condition (4.38) holds for
such that condition (4.38) holds for  one has
one has 
Proof.

Proof of estimate (4.39) follows directly from Theorem B.

Indeed from (4.38) and results of [1] on diagonal map in Bergman classes we have  It remains to apply Theorem A.
It remains to apply Theorem A.

For the proof of  we use Theorem 4.6 and get the result we need.
we use Theorem 4.6 and get the result we need.
For the proof of  we use the same argument as in the proof of part (2.11). Namely first from (4.38) and from a Diagonal map theorem on
we use the same argument as in the proof of part (2.11). Namely first from (4.38) and from a Diagonal map theorem on  classes from [1] we get
classes from [1] we get  It remains to apply Theorem A.
It remains to apply Theorem A.
Remark 4.10.
Note Proposition 4.9 is obvious for 
We give only a sketch of the proof of the following result. It is based completely on a technique we developed above.
Proposition 4.11.

Let  then the following assertions are true: If
then the following assertions are true: If  then
then

If  then
then 

Let  If
If  then
then  Moreover the reverse is also true if condition (4.38) holds for
Moreover the reverse is also true if condition (4.38) holds for  then
then 
The proof of first part of Proposition 4.11 follows from (4.35), (4.36) and Lemma 2.5 directly. The reverse assertion follows from Theorem B  and estimate
and estimate

which can obtained from one dimensional result by induction.
The proof of second part of Proposition 4.11 can be obtained from Theorem A and results on diagonal map on Hardy classes  from [1] similarly as the proof of Proposition 4.9. For
from [1] similarly as the proof of Proposition 4.9. For  part
part  is well known (e.g., see [1]) and
is well known (e.g., see [1]) and  follows from
follows from  since for
since for  condition (4.38) vanishes by Bergman representation formula.
condition (4.38) vanishes by Bergman representation formula.
Remark 4.12.
Theorem 4.6, Propositions 4.9 and 4.11 give an answer to a problem of Rudin (see [2]) to find traces of  Hardy classes on subvarieties other than diagonal
Hardy classes on subvarieties other than diagonal  Note that in [11] Clark solved this problem for subvarietes of
Note that in [11] Clark solved this problem for subvarietes of  based on finite Blaschke products.
based on finite Blaschke products.
References
Djrbashian AE, Shamoian FA: Topics in the Theory of Apα Spaces, Teubner Texts in Mathematics. Volume 105. Teubner, Leipzig, Germany; 1988.
Rudin W: Function Theory in Polydiscs. W. A. Benjamin, New York, NY, USA; 1969:vii+188.
Shamoyan R, Li S: On some properties of a differential operator on the polydisk. Banach Journal of Mathematical Analysis 2009,3(1):68–84.
Shamoian FA: Embedding theorems and characterization of traces in the spaces . Matematicheskii Sbornik 1978,107(3):709–725.
Ortega JM, Fàbrega J: Hardy's inequality and embeddings in holomorphic Triebel-Lizorkin spaces. Illinois Journal of Mathematics 1999,43(4):733–751.
Jevtić M, Pavlović M, Shamoyan RF: A note on the diagonal mapping in spaces of analytic functions in the unit polydisc. Publicationes Mathematicae Debrecen 2009,74(1–2):45–58.
Shapiro JH: Mackey topologies, reproducing kernels, and diagonal maps on the Hardy and Bergman spaces. Duke Mathematical Journal 1976,43(1):187–202. 10.1215/S0012-7094-76-04316-7
Ren G, Shi J: The diagonal mapping in mixed norm spaces. Studia Mathematica 2004,163(2):103–117. 10.4064/sm163-2-1
Amar E, Menini C: A counterexample to the corona theorem for operators on . Pacific Journal of Mathematics 2002,206(2):257–268. 10.2140/pjm.2002.206.257
Shamoyan R: On the action of Hankel operators in bidisk and subspaces in connected with inner functions in the unit disk. Comptes Rendus de l'Académie Bulgare des Sciences 2007,60(9):929–934.
Clark DN: Restrictions of functions in the polydisk. American Journal of Mathematics 1988,110(6):1119–1152. 10.2307/2374688
Guliev VS, Lizorkin PI: Classes of holomorphic and harmonic functions in a polydisk in connection with their boundary values. Trudy Matematicheskogo Instituta imeni V. A. Steklova 1993, 204: 137–159.
Shamoyan RF: On quasinorms of functions from holomorphic Lizorkin Triebel type spaces on subframe and polydisk. In Sympozium Fourier Series and Application, Conference Materials, 2002. Rostov Na Donu; 54–55.
Carleson L: A counter example for measures bounded in for the bidisc. Institut Mittag-Leffler; 1974.
Wu Z: Carleson measures and multipliers for Dirichlet spaces. Journal of Functional Analysis 1999,169(1):148–163. 10.1006/jfan.1999.3490
Mazya VG: Sobolev Spaces, Springer Series in Soviet Mathematics. Springer, Berlin, Germany; 1985:xix+486.
Acknowledgment
The authors sincerely thank Trieu Le for valuable discussions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Shamoyan, R.F., Mihić, O.R. Analytic Classes on Subframe and Expanded Disk and the 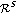 Differential Operator in Polydisk.
J Inequal Appl 2009, 353801 (2009). https://doi.org/10.1155/2009/353801
Differential Operator in Polydisk.
J Inequal Appl 2009, 353801 (2009). https://doi.org/10.1155/2009/353801
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/353801
 we can step by step repeat the same procedure with
we can step by step repeat the same procedure with  instead of
instead of  and the condition on
and the condition on 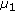 will be replaced by weaker condition
will be replaced by weaker condition 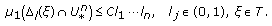
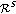 Operators and Inequalities Connecting Classes on Polydisk, Subframe, and Expanded Disk
Operators and Inequalities Connecting Classes on Polydisk, Subframe, and Expanded Disk