- Research Article
- Open access
- Published:
Some Inequalities for the 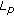 -Curvature Image
-Curvature Image
Journal of Inequalities and Applications volume 2009, Article number: 320786 (2009)
Abstract
Lutwak introduced the notion of  -curvature image and proved an inequality for the volumes of convex body and its
-curvature image and proved an inequality for the volumes of convex body and its  -curvature image. In this paper, we first give an monotonic property of
-curvature image. In this paper, we first give an monotonic property of  -curvature image. Further, we establish two inequalities for the
-curvature image. Further, we establish two inequalities for the  -curvature image and its polar, respectively. Finally, an inequality for the volumes of
-curvature image and its polar, respectively. Finally, an inequality for the volumes of  -projection body and
-projection body and  -curvature image is obtained.
-curvature image is obtained.
1. Introduction
Let  denote the set of convex bodies (compact, convex subsets with nonempty interiors) in Euclidean space
denote the set of convex bodies (compact, convex subsets with nonempty interiors) in Euclidean space  , for the set of convex bodies containing the origin in their interiors and the set of origin-symmetric convex bodies in
, for the set of convex bodies containing the origin in their interiors and the set of origin-symmetric convex bodies in  , we, respectively, write
, we, respectively, write  and
and  . Let
. Let  denote the unit sphere in
denote the unit sphere in  , and denote by
, and denote by  the
the  -dimensional volume of body
-dimensional volume of body  , for the standard unit ball
, for the standard unit ball  in
in  , and denote
, and denote  . The groups of nonsingular linear transformations and the group of special linear transformations are denoted by
. The groups of nonsingular linear transformations and the group of special linear transformations are denoted by  and
and  , respectively.
, respectively.
Suppose that  is the set of real numbers. If
is the set of real numbers. If  , then its support function,
, then its support function,  :
: 

 , is defined by (see [1, page 16])
, is defined by (see [1, page 16])

where  denotes the standard inner product of
denotes the standard inner product of  and
and  .
.
A convex body  is said to have a curvature function
is said to have a curvature function  , if its surface area measure
, if its surface area measure  is absolutely continuous with respect to spherical Lebesgue measure
is absolutely continuous with respect to spherical Lebesgue measure  , and
, and

For  , and real
, and real  , the
, the  -surface area measure,
-surface area measure,  , of
, of  is defined by (see [2, 3])
is defined by (see [2, 3])

Equation (1.3) is also called Radon-Nikodym derivative, and the measure  is absolutely continuous with respect to surface area measure
is absolutely continuous with respect to surface area measure  .
.
A convex body  is said to have a
is said to have a  -curvature function (see [2])
-curvature function (see [2])  , if its
, if its  -surface area measure
-surface area measure  is absolutely continuous with respect to spherical Lebesgue measure
is absolutely continuous with respect to spherical Lebesgue measure  , and
, and

If  is a compact star shaped (about the origin) in
is a compact star shaped (about the origin) in  , its radial function,
, its radial function,  , is defined by (see [1, page 18])
, is defined by (see [1, page 18])

If  is positive and continuous,
is positive and continuous,  will be called a star body (about the origin). Let
will be called a star body (about the origin). Let  denote the set of star bodies (about the origin) in
denote the set of star bodies (about the origin) in  . Two star bodies
. Two star bodies  and
and  are said to be dilates (of one another) if
are said to be dilates (of one another) if  is independent of
is independent of  .
.
For the radial function, if  , then (see [1, page 18])
, then (see [1, page 18])

From (1.6), we have that, for  ,
,

Let  ,
,  denote the set of all bodies in
denote the set of all bodies in  ,
,  , respectively, that have a positive continuous curvature function.
, respectively, that have a positive continuous curvature function.
Lutwak in [2] showed the notion of  -curvature image as follows. For each
-curvature image as follows. For each  and real
and real  , define
, define  , the
, the  -curvature image of
-curvature image of  , by
, by

Note that, for  , this definition differs from the definition of classical curvature image (see [2]). For the study of classical curvature image [1, 4–7].
, this definition differs from the definition of classical curvature image (see [2]). For the study of classical curvature image [1, 4–7].
Further, he proved that if  and
and , then
, then

with equality if and only if
 is an ellipsoid centered at the origin.
is an ellipsoid centered at the origin.
In this paper, we continuously study the  -curvature image for convex bodies. First, we give a monotonic property of
-curvature image for convex bodies. First, we give a monotonic property of  -curvature image as follows.
-curvature image as follows.
Theorem 1.1.
If  ,
,  , and
, and  , then
, then

with equality for  if and only if
if and only if  and
and  are dilates, for
are dilates, for  if and only if
if and only if  , and for
, and for  if and only if
if and only if  and
and  are translation.
are translation.
Next, we establish an inequality for the  -curvature image as follows.
-curvature image as follows.
Theorem 1.2.
If  , and
, and  , then
, then

with equality if and only if  is an ellipsoid.
is an ellipsoid.
Further, we get the following inequality for the polar of the  -curvature image.
-curvature image.
Theorem 1.3.
If  ,
,  , and
, and  , then
, then

with equality for  if and only if
if and only if  and
and  are dilates, and for
are dilates, and for  if and only if
if and only if  and
and  are homothetic.
are homothetic.
Here  denote the polar of
denote the polar of  , rather than
, rather than  . Compare with inequality (1.9), we see that inequality (1.12) may be regarded as a dual form of inequality (1.9).
. Compare with inequality (1.9), we see that inequality (1.12) may be regarded as a dual form of inequality (1.9).
Finally, we obtain an interesting inequality for the  -curvature image and
-curvature image and  -projection body
-projection body  as follows.
as follows.
Theorem 1.4.
If  ,
,  , then
, then

with equality if and only if  is an ellipsoid centered at the origin.
is an ellipsoid centered at the origin.
2. Preliminaries
2.1. Polar of Convex Body
If  , the polar body of
, the polar body of  ,
,  , is defined by (see [1, page 20])
, is defined by (see [1, page 20])

From the definition (2.1), we know that if  , then the support and radial functions of
, then the support and radial functions of  , the polar body of
, the polar body of  , are defined, respectively, by (see [1])
, are defined, respectively, by (see [1])

The Blaschke-Santaló inequality can be stated that (see [1] or [7]): If , then
, then

with equality if and only if is an ellipsoid.
is an ellipsoid.
2.2. 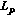 -Mixed Volume
-Mixed Volume
For  and
and  , the Firey
, the Firey  -combination
-combination  is defined by (see [8])
is defined by (see [8])

where " " in
" in  denotes the Firey scalar multiplication.
denotes the Firey scalar multiplication.
If  in
in  , then for
, then for  , the
, the  -mixed volume,
-mixed volume,  , of the
, of the  and
and  is defined by (see [9])
is defined by (see [9])

Corresponding to each  , there is a positive Borel measure,
, there is a positive Borel measure,  , on
, on  such that (see [9])
such that (see [9])

for each  . The measure
. The measure  is just the
is just the  -surface area measure of
-surface area measure of  .
.
From the formula (2.6) and definition (1.3), we immediately get that

The  -Minkowski inequality states that (see [9]) if
-Minkowski inequality states that (see [9]) if  and
and  then
then

with equality for  if and only if
if and only if  and
and  are dilates, and for
are dilates, and for  if and only if
if and only if  and
and  are homothetic.
are homothetic.
2.3.  -Dual Mixed Volume
-Dual Mixed Volume
For  , and
, and  , the
, the  -harmonic radial combination
-harmonic radial combination  is the star body whose radial function is defined by (see [2])
is the star body whose radial function is defined by (see [2])

Note that here " " and the Firey scalar multiplication "
" and the Firey scalar multiplication " " are different.
" are different.
If  , for
, for  , the
, the  -dual mixed volume,
-dual mixed volume,  , of the
, of the  and
and  is defined by (see [2])
is defined by (see [2])

The definition above and the polar coordinate formula for volume give the following integral representation of the  -dual mixed volume
-dual mixed volume  of
of  :
:

where the integration is with respect to spherical Lebesgue measure  on
on  .
.
From the formula (2.11), it follows immediately that, for each  and
and  ,
,

The Minkowski inequality for the  -dual mixed volume
-dual mixed volume  is that if
is that if  and
and  (see [2]), then
(see [2]), then

with equality if and only if  and
and  are dilates.
are dilates.
2.4. 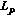 -Affine Surface Area
-Affine Surface Area
Lutwak in [2] showed that for each  and
and  , the
, the  -affine surface area,
-affine surface area,  , of
, of  can be defined by
can be defined by

For  ,
,  is just classical affine surface area
is just classical affine surface area  by Leichtweiβ (see [4]). Further, Lutwak proved that if
by Leichtweiβ (see [4]). Further, Lutwak proved that if  and
and  , then the
, then the  -affine surface area of
-affine surface area of  has the integral representation
has the integral representation

2.5. 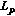 -Projection Body
-Projection Body
The notion of  -projection body is shown by Lutwak et al. (see [10]). For
-projection body is shown by Lutwak et al. (see [10]). For  and
and  , the
, the  -projection body,
-projection body,  , of
, of  is the origin-symmetric convex body whose support function is given by
is the origin-symmetric convex body whose support function is given by

for all  . Here
. Here  is just the
is just the  -surface area measure of
-surface area measure of  , and
, and

2.6. 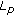 -Centroid Body
-Centroid Body
Lutwak and Zhang in [11] introduced the notion of  -centroid body. For each compact star-shaped body about the origin
-centroid body. For each compact star-shaped body about the origin  and for real number
and for real number  , the polar of
, the polar of  -centroid body,
-centroid body,  (rather than
(rather than  ), of
), of  is the origin-symmetric convex body, whose radial function is defined by [11]
is the origin-symmetric convex body, whose radial function is defined by [11]

for all  , where
, where  satisfy (2.17).
satisfy (2.17).
From definition (2.18) and equality (2.2), if  , then the
, then the  -centroid body
-centroid body  of
of  is the origin-symmetric convex body whose support function is given by
is the origin-symmetric convex body whose support function is given by

for all  .
.
3. The Proof of Theorems
In order to prove our theorems, the following lemmas are essential.
Lemma 3.1.
If  ,
,  and the constant
and the constant  , then
, then

Proof.
For  , from (1.3) and (1.4), then
, from (1.3) and (1.4), then

this together with (1.7) and (1.8), and notice that  for
for  , we get that
, we get that

that is,

and this together with formula (2.12), we have that

Hence, from (3.4), then

and this yields (3.1).
If  , Lutwak (see [2]) proved that, for
, Lutwak (see [2]) proved that, for  ,
,

where  denotes the inverse of the transpose of
denotes the inverse of the transpose of  .
.
Now we rewrite (3.1) as follows:

this together with (3.7) and the fact  , we easily get the following result.
, we easily get the following result.
Proposition 3.2.
If  ,
,  , then for
, then for  ,
,

Lemma 3.3 (see [2]).
If  ,
,  , then
, then

for all  .
.
Lemma 3.4.
If  ,
,  , then for all
, then for all  ,
,

Proof.
Taking  in (3.11), and using (2.12), we have that
in (3.11), and using (2.12), we have that  . Now inequality (2.13) gives
. Now inequality (2.13) gives  , with equality if and only if
, with equality if and only if  and
and  are dilates. Let
are dilates. Let  in (3.11), and get
in (3.11), and get  . Hence
. Hence  , and
, and  and
and  must be dilates. Thus
must be dilates. Thus  . In turn, when
. In turn, when  the result obviously is true.
the result obviously is true.
Proof of Theorem 1.1.
Since  , then from formula (2.11), we know
, then from formula (2.11), we know

for all  , with equality in (3.12) if and only if
, with equality in (3.12) if and only if  by (3.11). Using equality (3.10), then inequality (3.12) can be rewritten
by (3.11). Using equality (3.10), then inequality (3.12) can be rewritten

for all  . Let
. Let  , together with (2.7) and
, together with (2.7) and  -Minkowski inequality (2.8), we have
-Minkowski inequality (2.8), we have

Thus

and this is just inequality (1.10).
According to the conditions of equality that hold in inequalities (3.12) and (2.8), we know that equality holds in inequality (1.10) for  if and only if
if and only if  and
and  are dilates and
are dilates and  , and for
, and for  if and only if
if and only if  and
and  are homothetic and
are homothetic and  .
.
For the case  of equality that holds in (1.10), we may suppose
of equality that holds in (1.10), we may suppose  (
( ), and together with
), and together with  , then
, then  . Thus, from (3.1), we have
. Thus, from (3.1), we have  . Hence
. Hence  when
when  , this means that if
, this means that if  then
then  . For
. For  , we easily see that
, we easily see that  and
and  are dilates that impliy
are dilates that impliy  . So we know that equality holds in inequality (1.10) for
. So we know that equality holds in inequality (1.10) for  if and only if
if and only if  and
and  are dilates, and for
are dilates, and for  if and only if
if and only if  .
.
For the case  of equality that holds in (1.10), we may take
of equality that holds in (1.10), we may take  (
( ), then
), then

But  , then
, then  by (1.2). By this together with (2.15) and (3.10), we have
by (1.2). By this together with (2.15) and (3.10), we have  and
and  , respectively. Thus, from the definition (1.8), we obtain that
, respectively. Thus, from the definition (1.8), we obtain that

hence

From (3.18) and (3.1), equality (3.16) can be rewritten as follows:

and this gives  , that is,
, that is,  when
when  . Therefore, we see that equality holds in inequality (1.10) for
. Therefore, we see that equality holds in inequality (1.10) for  if and only if
if and only if  and
and  are translation.
are translation.
Proof of Theorem 1.2.
Let  in (3.10), together with (2.7) and (2.13), we have that
in (3.10), together with (2.7) and (2.13), we have that

with equality in inequality (3.20) if and only if  and
and  are dilates.
are dilates.
From this, and using the Blaschke-Santaló inequality (2.3), then

and equality holds in second inequality of (3.21) if and only if  is an ellipsoid.
is an ellipsoid.
From (3.21), we immediately obtain inequality (1.11). According to the conditions of equality that hold in (3.20) and second inequality of (3.21), we get equality in (1.11) if and only if  is an ellipsoid.
is an ellipsoid.
Proof of Theorem 1.3.
Taking  in (3.10), and using (2.12), then
in (3.10), and using (2.12), then

From (3.22), and together with inequality (2.8), we have

this inequality immediately gives (1.12). According to equality conditions of inequality (2.8), we get equality in (1.12) for  if and only if
if and only if  and
and  are dilates, and for
are dilates, and for  if and only if
if and only if  and
and  are homothetic.
are homothetic.
The proof of Theorem 1.4 requires the following two lemmas.
Lemma 3.5.
If  ,
,  , then
, then

Note that the proof of Lemma 3.5 can be found in [12]. Here, for the sake of completeness, we present the proof as follows.
Proof.
Using the definitions (2.16), (1.4), and (1.8), we have

for all  . According to (2.19), we also have that, for all
. According to (2.19), we also have that, for all  ,
,

But (2.17) gives  hence from (3.25) and (3.26), we obtain
hence from (3.25) and (3.26), we obtain

for all  . Thus
. Thus  .
.
Lemma 3.6 ([10] ( -Busemann-Petty centroid inequality)).
-Busemann-Petty centroid inequality)).
If  ,
,  , then
, then

with equality if and only if  is an ellipsoid centered at the origin.
is an ellipsoid centered at the origin.
Proof of Theorem 1.4.
From (3.28) and (3.24), we immediately get inequality (1.13). According to the case of equality that holds in (3.28), we see equality in (1.13) if and only if  is an ellipsoid centered at the origin.
is an ellipsoid centered at the origin.
References
Gardner RJ: Geometric Tomography, Encyclopedia of Mathematics and Its Applications. Volume 58. 2nd edition. Cambridge University Press, Cambridge, UK; 2006.
Lutwak E: The Brunn-Minkowski-Firey theory II: affine and geominimal surface areas. Advances in Mathematics 1996,118(2):244–294. 10.1006/aima.1996.0022
Lutwak E, Yang D, Zhang GY: John ellipsoids. Proceedings of the London Mathematical Society 2005,90(2):497–520. 10.1112/S0024611504014996
Leichtweiß K: Affine Geometry of Convex Bodies. Johann Ambrosius Barth, Heidelberg, Germany; 1998.
Lutwak E: On some affine isoperimetric inequalities. Journal of Differential Geometry 1986, 56: 1–13.
Petty CM: Affine isoperimetric problems. Annals of the New York Academy of Sciences 1985, 440: 113–127. 10.1111/j.1749-6632.1985.tb14545.x
Schneider R: Convex Bodies: The Brunn-Minkowski Theory. Volume 44. Cambridge University Press, Cambridge, UK; 1993.
Firey WJ: -means of convex bodies. Mathematica Scandinavica 1962, 10: 17–24.
Lutwak E: The Brunn-Minkowski-Firey theory I: mixed volumes and the minkowski problem. Journal of Differential Geometry 1993,38(1):131–150.
Lutwak E, Yang D, Zhang GY: affine isoperimetric inequalities. Journal of Differential Geometry 2000,56(1):111–132.
Lutwak E, Zhang GY: Blaschke-Santaló inequalities. Journal of Differential Geometry 1997,47(1):1–16.
Lv SJ, Leng GS: The -curvature images of convex bodies and -projection bodies. Proceedings of the Indian Academy of Sciences. Mathematical Sciences 2008,118(3):413–424. 10.1007/s12044-008-0032-6
Acknowledgment
This research is supported in part by the Natural Science Foundation of China (Grant no. 10671117), Academic Mainstay Foundation of Hubei Province of China (Grant no. D200729002), and Science Foundation of China Three Gorges University. The authors wish to thank the referees for their very helpful comments and suggestions on this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Weidong, W., Daijun, W. & Yu, X. Some Inequalities for the 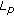 -Curvature Image.
J Inequal Appl 2009, 320786 (2009). https://doi.org/10.1155/2009/320786
-Curvature Image.
J Inequal Appl 2009, 320786 (2009). https://doi.org/10.1155/2009/320786
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/320786
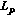 -Mixed Volume
-Mixed Volume -Dual Mixed Volume
-Dual Mixed Volume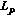 -Affine Surface Area
-Affine Surface Area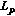 -Projection Body
-Projection Body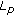 -Centroid Body
-Centroid Body