- Research Article
- Open access
- Published:
Perturbed Iterative Approximation of Solutions for Nonlinear General  -Monotone Operator Equations in Banach Spaces
-Monotone Operator Equations in Banach Spaces
Journal of Inequalities and Applications volume 2009, Article number: 290713 (2009)
Abstract
We introduce and study a new class of nonlinear general  -monotone operator equations with multivalued operator. By using Alber's inequalities, Nalder's results, and the new proximal mapping technique, we construct some new perturbed iterative algorithms with mixed errors for solving the nonlinear general
-monotone operator equations with multivalued operator. By using Alber's inequalities, Nalder's results, and the new proximal mapping technique, we construct some new perturbed iterative algorithms with mixed errors for solving the nonlinear general  -monotone operator equations and study the approximation-solvability of the nonlinear operator equations in Banach spaces. The results presented in this paper improve and generalize the corresponding results on strongly monotone quasivariational inclusions and nonlinear implicit quasivariational inclusions.
-monotone operator equations and study the approximation-solvability of the nonlinear operator equations in Banach spaces. The results presented in this paper improve and generalize the corresponding results on strongly monotone quasivariational inclusions and nonlinear implicit quasivariational inclusions.
1. Introduction
Let  be a real Banach space with the topological dual space of
be a real Banach space with the topological dual space of  , let
, let  be the pairing between
be the pairing between  and
and  , let
, let  denote the family of all subsets of
denote the family of all subsets of  and let
and let  denote the family of all nonempty closed bounded subsets of
denote the family of all nonempty closed bounded subsets of  . We denote by the
. We denote by the  for all
for all  and
and  . Let
. Let  ,
,  and
and  be nonlinear operators, and let
be nonlinear operators, and let  be a general
be a general  -monotone operator such that
-monotone operator such that  . We will consider the following nonlinear general
. We will consider the following nonlinear general  -monotone operator equation with multivalued operator.
-monotone operator equation with multivalued operator.
Find  such that
such that  and
and

where  is a constant and
is a constant and  is the proximal mapping associated with the general
is the proximal mapping associated with the general  -monotone operator
-monotone operator  due to Cui et al. [1].
due to Cui et al. [1].
It is easy to see that the problem (1.1) is equivalent to the problem of finding  such that
such that

Example 1.1.
If  , then the problem (1.1) is equivalent to finding
, then the problem (1.1) is equivalent to finding  such that
such that  and
and

Based on the definition of the proximal mapping  , (1.3) can be written as
, (1.3) can be written as

Example 1.2.
If  is a single-valued operator, then a special case of the problem (1.3) is to determine element
is a single-valued operator, then a special case of the problem (1.3) is to determine element  such that
such that

where  is defined by
is defined by  for all
for all  . The problem (1.5) was studied by Xia and Huang [2] when M is a general H-monotone mapping. Further, the problem (1.5) was studied by Peng et al. [3] if
. The problem (1.5) was studied by Xia and Huang [2] when M is a general H-monotone mapping. Further, the problem (1.5) was studied by Peng et al. [3] if  , the identity operator, and M is a multivalued maximal monotone mapping.
, the identity operator, and M is a multivalued maximal monotone mapping.
Example 1.3.
If  ,
,  , and
, and  are single-valued operators, and
are single-valued operators, and  for all
for all  , then the problem (1.3) reduces to finding an element
, then the problem (1.3) reduces to finding an element  such that
such that

which was considered by Verma [4, 5].
We note that for appropriate and suitable choices of  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  , it is easy to see that the problem (1.1) includes a number of quasivariational inclusions, generalized quasivariational inclusions, quasivariational inequalities, implicit quasivariational inequalities, complementarity problems, and equilibrium problems studied by many authors as special cases; see, for example, [4–7] and the references therein.
, it is easy to see that the problem (1.1) includes a number of quasivariational inclusions, generalized quasivariational inclusions, quasivariational inequalities, implicit quasivariational inequalities, complementarity problems, and equilibrium problems studied by many authors as special cases; see, for example, [4–7] and the references therein.
The study of such types of problems is motivated by an increasing interest to study the behavior and approximation of the solution sets for many important nonlinear problems arising in mechanics, physics, optimization and control, nonlinear programming, economics, finance, regional structural, transportation, elasticity, engineering, and various applied sciences in a general and unified framework. It is well known that many authors have studied a number of nonlinear variational inclusions and many systems of variational inequalities, variational inclusions, complementarity problems, and equilibrium problems by using the resolvent operator technique, which is a very important method to find solutions of variational inequality and variational inclusion problems; see, for example, [1–15] and the references therein.
On the other hand, Verma [4, 5] introduced the concept of  -monotone mappings, which generalizes the well-known general class of maximal monotone mappings and originates way back from an earlier work of the Verma [7]. Furthermore, motivated and inspired by the works of Xia and Huang [2], Cui et al. [1] introduced first a new class of general
-monotone mappings, which generalizes the well-known general class of maximal monotone mappings and originates way back from an earlier work of the Verma [7]. Furthermore, motivated and inspired by the works of Xia and Huang [2], Cui et al. [1] introduced first a new class of general  -monotone operators in Banach spaces, studied some properties of general
-monotone operators in Banach spaces, studied some properties of general  -monotone operator, and defined a new proximal mapping associated with the general
-monotone operator, and defined a new proximal mapping associated with the general  -monotone operator.
-monotone operator.
Inspired and motivated by the research works going on this field, the purpose of this paper is to introduce the new class of nonlinear general  -monotone operator equation with multivalued operator. By using Alber's inequalities, Nalder's results, and the new proximal mapping technique, some new perturbed iterative algorithms with mixed errors for solving the nonlinear general
-monotone operator equation with multivalued operator. By using Alber's inequalities, Nalder's results, and the new proximal mapping technique, some new perturbed iterative algorithms with mixed errors for solving the nonlinear general  -monotone operator equations will be constructed, and applications of general
-monotone operator equations will be constructed, and applications of general  -monotone operators to the approximation-solvability of the nonlinear operator equations in Banach spaces will be studied. The results presented in this paper improve and extend some corresponding results in recent literature.
-monotone operators to the approximation-solvability of the nonlinear operator equations in Banach spaces will be studied. The results presented in this paper improve and extend some corresponding results in recent literature.
2. Preliminaries
In this paper, we will use the following definitions and lemmas.
Definition 2.1.
Let  ,
,  , and
, and  be single-valued operators. Then
be single-valued operators. Then
(i) is
is  -strongly monotone, if there exists a positive constant
-strongly monotone, if there exists a positive constant  such that
such that

(ii) is
is  -Lipschitz continuous, if there exists a constant
-Lipschitz continuous, if there exists a constant  such that
such that

(iii) is
is  -strongly accretive if for any
-strongly accretive if for any  , there exist
, there exist  and a positive constant
and a positive constant  such that
such that

where the generalized duality mapping  is defined by
is defined by

(iv) is
is  -relaxed cocoercive with respect to
-relaxed cocoercive with respect to  , if for all
, if for all  , there exist positive constants
, there exist positive constants  and
and  such that
such that

-
(1)
Consider an
 -strongly monotone (and hence
-strongly monotone (and hence  -expanding) operator
-expanding) operator 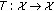 . Then
. Then 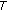 is
is  -relaxed cocoercive with respect to
-relaxed cocoercive with respect to 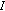 .
. -
(2)
Very
 -cocoercive operator is
-cocoercive operator is 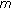 -relaxed cocoercive, while each
-relaxed cocoercive, while each  -strongly monotone mapping is
-strongly monotone mapping is 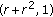 -relaxed cocoercive with respect to
-relaxed cocoercive with respect to 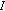 .
.
Remark 2.3.
The notion of the cocoercivity is applied in several directions, especially to solving variational inequality problems using the auxiliary problem principle and projection methods [5], while the notion of the relaxed cocoercivity is more general than the strong monotonicity as well as cocoercivity. Several classes of relaxed cocoercive variational inequalities have been studied in [4, 5].
Definition 2.4.
A multivalued operator  is said to be
is said to be
(i)maximal monotone if, for any  ,
,  ,
,

(ii) -relaxed monotone if, for any
-relaxed monotone if, for any  ,
,  , and
, and  , there exists a positive constant
, there exists a positive constant  such that
such that

(iii) -
- -Lipschitz continuous, if there exists a constant
-Lipschitz continuous, if there exists a constant  such that
such that

where  is the Hausdorff pseudometric, that is,
is the Hausdorff pseudometric, that is,

Note that if the domain of  is restricted to closed bounded subsets
is restricted to closed bounded subsets  , then
, then  is the Hausdorff metric.
is the Hausdorff metric.
Definition 2.5.
A single-valued operator  is said to be
is said to be
(i)coercive if

(ii)hemicontinuous if, for any fixed  , the function
, the function  is continuous at
is continuous at  .
.
We remark that the uniform convexity of the space  means that for any given
means that for any given  , there exists
, there exists  such that for all
such that for all  ,
,  ,
,  and
and  ensure the inequality
ensure the inequality  . The function
. The function

is called the modulus of the convexity of the space  .
.
The uniform smoothness of the space  means that for any given
means that for any given  , there exists
, there exists  such that
such that  holds. The function
holds. The function  defined by
defined by

is called the modulus of the smoothness of the space  .
.
We also remark that the space  is uniformly convex if and only if
is uniformly convex if and only if  for all
for all  , and it is uniformly smooth if and only if
, and it is uniformly smooth if and only if  Moreover,
Moreover,  is uniformly convex if and only if
is uniformly convex if and only if  is uniformly smooth. In this case,
is uniformly smooth. In this case,  is reflexive by the Milman theorem. A Hilbert space is uniformly convex and uniformly smooth. The proof of the following inequalities can be found, for example, in page 24 of Alber [16].
is reflexive by the Milman theorem. A Hilbert space is uniformly convex and uniformly smooth. The proof of the following inequalities can be found, for example, in page 24 of Alber [16].
Lemma 2.6.
Let  be a uniformly smooth Banach space, and let
be a uniformly smooth Banach space, and let  be the normalized duality mapping from
be the normalized duality mapping from  into
into  . Then, for all
. Then, for all  , we have
, we have
(i) ;
;
(ii) , where
, where  .
.
Definition 2.7.
Let  be a Banach space with the dual space
be a Banach space with the dual space  ,
,  be a nonlinear operator, and
be a nonlinear operator, and  be a multivalued operator. The map
be a multivalued operator. The map  is said to be general
is said to be general  -monotone if
-monotone if  is
is  -relaxed monotone and
-relaxed monotone and  holds for every
holds for every  .
.
This is equivalent to stating that  is general
is general  -monotone if.
-monotone if.
(i) is
is  -relaxed monotone;
-relaxed monotone;
(ii) is maximal monotone for every
is maximal monotone for every  .
.
Remark 2.8.
-
(1)
If
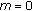 , that is,
, that is,  is
is  -relaxed monotone, then the general
-relaxed monotone, then the general  -monotone operators reduce to general
-monotone operators reduce to general 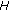 -monotone operators (see, e.g., [1, 2]).
-monotone operators (see, e.g., [1, 2]). -
(2)
If
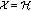 is a Hilbert space, then the general
is a Hilbert space, then the general 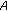 -monotone operator reduces to the
-monotone operator reduces to the 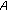 -monotone operator in Verma [7]. Therefore, the class of general
-monotone operator in Verma [7]. Therefore, the class of general  -monotone operators provides a unifying frameworks for classes of maximal monotone operators,
-monotone operators provides a unifying frameworks for classes of maximal monotone operators, 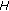 -monotone operators,
-monotone operators, 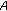 -monotone operators, and general
-monotone operators, and general 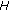 -monotone operators. For details about these operators, we refer the reader to [1, 2, 7] and the references therein.
-monotone operators. For details about these operators, we refer the reader to [1, 2, 7] and the references therein.
Example 2.9.
Let  be a reflexive Banach space with the dual space
be a reflexive Banach space with the dual space  ,
,  a maximal monotone mapping, and
a maximal monotone mapping, and  a bounded, coercive, hemicontinuous, and relaxed monotone mapping. Then for any given
a bounded, coercive, hemicontinuous, and relaxed monotone mapping. Then for any given  , it follows from Theorem 3.1 in page 401 of Guo [10] that
, it follows from Theorem 3.1 in page 401 of Guo [10] that  . This shows that
. This shows that  is a general
is a general  -monotone operator.
-monotone operator.
Example 2.10 (see [4]).
Let  be a reflexive Banach space with
be a reflexive Banach space with  its dual, and let
its dual, and let  be
be  -strongly monotone. Let
-strongly monotone. Let  be locally Lipschitz such that
be locally Lipschitz such that  is
is  -relaxed monotone. Then
-relaxed monotone. Then  is
is  -monotone, which is equivalent to stating that
-monotone, which is equivalent to stating that  is pseudomonotone (and in fact, maximal monotone).
is pseudomonotone (and in fact, maximal monotone).
Lemma 2.11 (see [1]).
Let  be a reflexive Banach space with the dual space
be a reflexive Banach space with the dual space  , let
, let  be a nonlinear operator, and let
be a nonlinear operator, and let  be a general
be a general  -monotone operator. Then the proximal mapping
-monotone operator. Then the proximal mapping  is
is
(i) -Lipschitz continuous when
-Lipschitz continuous when  is
is  -strongly monotone with
-strongly monotone with  and
and  ;
;
(ii) -Lipschitz continuous if
-Lipschitz continuous if  is a strictly monotone operator and
is a strictly monotone operator and  is an
is an  -strongly monotone operator.
-strongly monotone operator.
3. Perturbed Algorithms and Convergence
Now we will consider some new perturbed algorithms for solving the nonlinear general  -monotone operator equation problem (1.1) or (1.2) by using the proximal mapping technique associated with the general
-monotone operator equation problem (1.1) or (1.2) by using the proximal mapping technique associated with the general  -monotone operators and the convergence of the sequences given by the algorithms.
-monotone operators and the convergence of the sequences given by the algorithms.
Lemma 3.1.
Let  ,
,  ,
,  ,
,  ,
,  , and
, and  be the same as in (1.1). Then the following propositions are equivalent.
be the same as in (1.1). Then the following propositions are equivalent.
(1) is a solution of the problem (1.1), where
is a solution of the problem (1.1), where  and
and  .
.
(2) is the fixed-point of the function
is the fixed-point of the function  defined by
defined by

where  is a constant.
is a constant.
(3) is a solution of the following equation system:
is a solution of the following equation system:

where  ,
,  and
and  .
.
Lemma 3.2 (see [17]).
Let  and
and  be three nonnegative real sequences satisfying the following condition. There exists a natural number
be three nonnegative real sequences satisfying the following condition. There exists a natural number  such that
such that

where  ,
,  ,
,  ,
,  . Then
. Then  .
.
Algorithm 3.3.
Step 1.
Choose an arbitrary initial point  .
.
Step 2.
Take any  for
for 
Step 3.
Choose sequences  ,
,  ,
,  and
and  such that for
such that for  ,
,  are two sequences in
are two sequences in  and
and 
 and
and  are error sequences in
are error sequences in  to take into account a possible inexact computation of the operator point, which satisfies the following conditions:
to take into account a possible inexact computation of the operator point, which satisfies the following conditions:
(i) ;
;
(ii) ;
;
(iii) .
.
Step 4.
Let  satisfy
satisfy

where  is a constant.
is a constant.
Step 5.
If  ,
,  ,
,  ,
,  ,
,  , and
, and  (
( ) satisfy (3.4) to sufficient accuracy, stop; otherwise, set
) satisfy (3.4) to sufficient accuracy, stop; otherwise, set  and return to Step 2.
and return to Step 2.
Algorithm 3.4.
For any  ,
,  , compute the iterative sequence
, compute the iterative sequence  by
by

where  ,
,  ,
,  ,
,  , and
, and  are the same as in Algorithm 3.3.
are the same as in Algorithm 3.3.
Theorem 3.5.
Let  be a uniformly smooth Banach space with
be a uniformly smooth Banach space with  for some
for some  , and let
, and let  be the dual space of
be the dual space of  . Let
. Let  be
be  -strongly monotone and
-strongly monotone and  -Lipschitz continuous, and let
-Lipschitz continuous, and let  be
be  -
- -Lipschitz continuous. Suppose that
-Lipschitz continuous. Suppose that  is
is  -relaxed cocoercive with respect to
-relaxed cocoercive with respect to  and
and  -Lipschitz continuous,
-Lipschitz continuous,  is
is  -strongly monotone and
-strongly monotone and  -Lipschitz continuous, and
-Lipschitz continuous, and  is general
is general  -monotone, where
-monotone, where  is defined by
is defined by  for all
for all  . If, in addition, there exist constants
. If, in addition, there exist constants  and
and  such that
such that

then the following results hold:
-
(1)
the solution set of the problem (1.1) is nonempty;
-
(2)
the iterative sequence
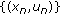 generated by Algorithm 3.3 converges strongly to the solution
generated by Algorithm 3.3 converges strongly to the solution 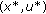 of the problem (1.1).
of the problem (1.1).
Proof.
Setting a multivalued function  to be the same as (3.1), then we can prove that
to be the same as (3.1), then we can prove that  is a multivalued contractive operator.
is a multivalued contractive operator.
In fact, for any  and any
and any  , there exists
, there exists  such that
such that

Note that  it follows from Nadler's result [18] that there exists
it follows from Nadler's result [18] that there exists  such that
such that

Letting

then we have  . The
. The  -strongly monotonicity and
-strongly monotonicity and  -Lipschitz continuity of
-Lipschitz continuity of  , the
, the  -
- -Lipschitz continuity of
-Lipschitz continuity of  , the
, the  -relaxed cocoercivity with respect to
-relaxed cocoercivity with respect to  and
and  -Lipschitz continuity of
-Lipschitz continuity of  , and the
, and the  -Lipschitz continuity of
-Lipschitz continuity of  , Lemma 2.6, and the inequality (3.8) imply that
, Lemma 2.6, and the inequality (3.8) imply that

Thus, it follows from (3.4) and Lemma 2.11 that

where

It follows from condition (3.6) that  . Hence, from (3.11), we get
. Hence, from (3.11), we get

Since  is arbitrary, we obtain
is arbitrary, we obtain  . By using same argument, we can prove
. By using same argument, we can prove  . It follows from the definition of the Hausdorff metric
. It follows from the definition of the Hausdorff metric  on
on  that
that

and so  is a multivalued contractive mapping. By a fixed-point theorem of Nadler [18], the definition of
is a multivalued contractive mapping. By a fixed-point theorem of Nadler [18], the definition of  and (3.2), now we know that
and (3.2), now we know that  has a fixed-point
has a fixed-point  , that is,
, that is,  and there exists
and there exists  such that
such that

Hence, it follows from Lemma 3.1 that  is a solution of the problem (1.1), that is, the solution set of the problem (1.1) is nonempty.
is a solution of the problem (1.1), that is, the solution set of the problem (1.1) is nonempty.
Next, we prove the conclusion (2). Let  be a solution of problem (1.1). Then for all
be a solution of problem (1.1). Then for all  , we have
, we have

From Algorithm 3.3, the assumptions of the theorem 3.5 and Lemma 2.11, it follows that


Combining (3.17) and (3.18), we obtain

where  is the same as in (3.11). Since
is the same as in (3.11). Since  , we know that
, we know that  and (3.19) implies
and (3.19) implies

Since  , it follows from Lemma 3.2 that the sequence
, it follows from Lemma 3.2 that the sequence  strongly converges to
strongly converges to  . By
. By  ,
,  , and the
, and the  -Lipschitz continuity of
-Lipschitz continuity of  , we obtain
, we obtain

Thus,  is also strongly converges to
is also strongly converges to  . Therefore, the iterative sequence
. Therefore, the iterative sequence  generated by Algorithm 3.3 converges strongly to the solution
generated by Algorithm 3.3 converges strongly to the solution  of the problem (1.1) or (1.2). This completes the proof.
of the problem (1.1) or (1.2). This completes the proof.
Based on Theorem 3.3 in [2], we have the following comment.
Remark 3.6.
If  ,
,  is
is  -strongly accretive and
-strongly accretive and  -Lipschitz continuous,
-Lipschitz continuous,  is a strictly monotone and
is a strictly monotone and  -Lipschitz continuous operator,
-Lipschitz continuous operator,  is a general
is a general  -monotone and
-monotone and  -strongly monotone operator,
-strongly monotone operator,  is a single-valued operator and
is a single-valued operator and  is
is  -Lipschitz continuous, and
-Lipschitz continuous, and  is some constant such that
is some constant such that

then (3.6) holds.
Theorem 3.7.
Assume that  ,
,  ,
,  ,
,  ,
,  and
and  are the same as in Theorem 3.5. If there exist constants
are the same as in Theorem 3.5. If there exist constants  and
and  such that
such that

then there exists  such that
such that  is a solution of the problem (1.3), and the iterative sequence
is a solution of the problem (1.3), and the iterative sequence  generated by Algorithm 3.4 converges strongly to the solution
generated by Algorithm 3.4 converges strongly to the solution  of the problem (1.3).
of the problem (1.3).
Remark 3.8.
If  for
for  in Algorithm 3.4,
in Algorithm 3.4,  and
and  as the same in the problem (1.5), then the results of Theorem 3.4 obtained by Xia and Huang [2] also hold. For details, we can refer to [1, 2, 4, 5].
as the same in the problem (1.5), then the results of Theorem 3.4 obtained by Xia and Huang [2] also hold. For details, we can refer to [1, 2, 4, 5].
Remark 3.9.
If  or
or  or
or  in Algorithms 3.3 and 3.4, then the conclusions of Theorems 3.5 and 3.7 also hold, respectively. The results of Theorems 3.5 and 3.7 improve and generalize the corresponding results of [2, 4–9, 15, 17]. For other related works, we refer to [1–16] and the references therein.
in Algorithms 3.3 and 3.4, then the conclusions of Theorems 3.5 and 3.7 also hold, respectively. The results of Theorems 3.5 and 3.7 improve and generalize the corresponding results of [2, 4–9, 15, 17]. For other related works, we refer to [1–16] and the references therein.
References
Cui Y-S, Lan H-Y, Chen Y-C: On implicit fuzzy proximal dynamical systems involving general -monotone operators in Banach spaces. Proceedings of the 5th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD '08), October 2008, Jinan, China 1: 615–620.
Xia F-Q, Huang N-J: Variational inclusions with a general -monotone operator in Banach spaces. Computers & Mathematics with Applications 2007,54(1):24–30. 10.1016/j.camwa.2006.10.028
Ceng L-C, Guu S-M, Yao J-C: Iterative approximation of solutions for a class of completely generalized set-valued quasi-variational inclusions. Computers & Mathematics with Applications 2008,56(4):978–987. 10.1016/j.camwa.2008.01.026
Verma RU: Approximation-solvability of a class of -monotone variational inclusion problems. Journal of the Korean Society for Industrial and Applied Mathematics 2004,8(1):55–66.
Verma RU: -monotonicity and applications to nonlinear variational inclusion problems. Journal of Applied Mathematics and Stochastic Analysis 2004,2004(2):193–195. 10.1155/S1048953304403013
Cho YJ, Lan H-Y: A new class of generalized nonlinear multi-valued quasi-variational-like inclusions with -monotone mappings. Mathematical Inequalities & Applications 2007,10(2):389–401.
Verma RU: Nonlinear variational and constrained hemivariational inequalities involving relaxed operators. Zeitschrift für Angewandte Mathematik und Mechanik 1997,77(5):387–391. 10.1002/zamm.19970770517
Peng J-W, Wang Y, Shyu DS, Yao J-C: Common solutions of an iterative scheme for variational inclusions, equilibrium problems, and fixed point problems. Journal of Inequalities and Applications 2008, 2008:-15.
Ahmad R, Ansari QH: Generalized variational inclusions and -resolvent equations with -accretive operators. Taiwanese Journal of Mathematics 2007,11(3):703–716.
Guo DJ: Nonlinear Functional Analysis. 2nd edition. Shandong Science and Technology Press, Shandong, China; 2001.
Lan H-Y, Kim JH, Cho YJ: On a new system of nonlinear -monotone multivalued variational inclusions. Journal of Mathematical Analysis and Applications 2007,327(1):481–493. 10.1016/j.jmaa.2005.11.067
Lan H-Y, Cho YJ, Verma RU: On solution sensitivity of generalized relaxed cocoercive implicit quasivariational inclusions with -monotone mappings. Journal of Computational Analysis and Applications 2006,8(1):75–87.
Lan H-Y: Projection iterative approximations for a new class of general random implicit quasi-variational inequalities. Journal of Inequalities and Applications 2006, 2006:-17.
Lan H-Y, Cho YJ, Xie W: General nonlinear random equations with random multi-valued operator in Banach spaces. Journal of Inequalities and Applications 2009, 2009:-17.
Wang Z, Wu C: A system of nonlinear variational inclusions with -monotone mappings. Journal of Inequalities and Applications 2008, 2008:-6.
Alber YI: Metric and generalized projection operators in Banach spaces: properties and applications. In Theory and Applications of Nonlinear Operators of Accretive and Monotone Type, Lecture Notes in Pure and Applied Mathematics. Volume 178. Edited by: Kartsatos A. Marcel Dekker, New York, NY, USA; 1996:15–50.
Liu LS: Ishikawa and Mann iterative process with errors for nonlinear strongly accretive mappings in Banach spaces. Journal of Mathematical Analysis and Applications 1995,194(1):114–125. 10.1006/jmaa.1995.1289
Nadler SB Jr.: Multi-valued contraction mappings. Pacific Journal of Mathematics 1969, 30: 475–488.
Acknowledgments
The authors are grateful to Professor Ram U. Verma and the referees for their valuable comments and suggestions. This work was supported by the National Natural Science Foundation of China (60804065), the Scientific Research Fund of Sichuan Provincial Education Department (2006A106, 07ZB151), and the Sichuan Youth Science and Technology Foundation (08ZQ026-008).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wei, X., Lan, Hy. & Zhang, Xj. Perturbed Iterative Approximation of Solutions for Nonlinear General  -Monotone Operator Equations in Banach Spaces.
J Inequal Appl 2009, 290713 (2009). https://doi.org/10.1155/2009/290713
-Monotone Operator Equations in Banach Spaces.
J Inequal Appl 2009, 290713 (2009). https://doi.org/10.1155/2009/290713
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/290713
 -strongly monotone (and hence
-strongly monotone (and hence  -expanding) operator
-expanding) operator 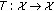 . Then
. Then 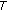 is
is  -relaxed cocoercive with respect to
-relaxed cocoercive with respect to 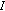 .
. -cocoercive operator is
-cocoercive operator is 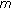 -relaxed cocoercive, while each
-relaxed cocoercive, while each  -strongly monotone mapping is
-strongly monotone mapping is 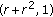 -relaxed cocoercive with respect to
-relaxed cocoercive with respect to 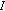 .
.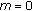 , that is,
, that is,  is
is  -relaxed monotone, then the general
-relaxed monotone, then the general  -monotone operators reduce to general
-monotone operators reduce to general 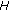 -monotone operators (see, e.g., [
-monotone operators (see, e.g., [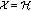 is a Hilbert space, then the general
is a Hilbert space, then the general 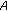 -monotone operator reduces to the
-monotone operator reduces to the 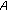 -monotone operator in Verma [
-monotone operator in Verma [ -monotone operators provides a unifying frameworks for classes of maximal monotone operators,
-monotone operators provides a unifying frameworks for classes of maximal monotone operators, 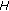 -monotone operators,
-monotone operators, 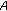 -monotone operators, and general
-monotone operators, and general 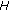 -monotone operators. For details about these operators, we refer the reader to [
-monotone operators. For details about these operators, we refer the reader to [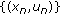 generated by Algorithm 3.3 converges strongly to the solution
generated by Algorithm 3.3 converges strongly to the solution 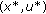 of the problem (1.1).
of the problem (1.1).