- Research Article
- Open access
- Published:
Perturbation Results on Semi-Fredholm Operators and Applications
Journal of Inequalities and Applications volume 2009, Article number: 284526 (2009)
Abstract
We give some results concerning stability in the Fredholm operators and Browder operators set, via the concept of measure of noncompactness. Moreover, we prove some localization results on the essential spectra of bounded operators on Banach space. As application, we describe the essential spectra of weighted shift operators. Finally, we describe the spectra of polynomially compact operators, and we use the obtained results to study the solvability for operator equations in Banach spaces.
1. Introduction
Throughout this paper,  denotes an infinite dimensional complex Banach space. We denote by
denotes an infinite dimensional complex Banach space. We denote by  the space of all bounded linear operators on
the space of all bounded linear operators on  The subspace of all compact operators of
The subspace of all compact operators of  is denoted by
is denoted by  . We write
. We write  for the null space and
for the null space and  for the range of
for the range of  . The nullity,
. The nullity,  of
of  is defined as the dimension of
is defined as the dimension of  and the deficiency,
and the deficiency,  of
of  is defined as the codimension of
is defined as the codimension of  in
in  . The set of upper (lower) semi-Fredholm operators are defined, respectively by
. The set of upper (lower) semi-Fredholm operators are defined, respectively by  and
and  and, respectively,
and, respectively,  We use
We use  for the set of Fredholm operators in
for the set of Fredholm operators in  , and
, and  for the set of semi-Fredholm operators in
for the set of semi-Fredholm operators in  . If
. If  then
then  is called the index of
is called the index of  . It is well known that the index is a continuous function on the set of semi-Fredholm operators.
. It is well known that the index is a continuous function on the set of semi-Fredholm operators.
Various notions of essential spectrum appear in the applications of spectral theory (see, e.g., [1, 2]). We use  for the spectrum of
for the spectrum of 
 for Wolf essential spectrum,
for Wolf essential spectrum,  for Schechter essential spectrum, and
for Schechter essential spectrum, and  for approximate point spectrum.
for approximate point spectrum.
Recall that  (resp.,
(resp.,  ), the ascent (resp., the descent) of
), the ascent (resp., the descent) of  , is the smallest nonnegative integer
, is the smallest nonnegative integer  such that
such that  (resp.
(resp.  ). If no such
). If no such  exists, then
exists, then  (resp.
(resp.  ). The sets of upper and lower semi-Browder operators are defined, respectively by
). The sets of upper and lower semi-Browder operators are defined, respectively by 
 The set of Browder operators on
The set of Browder operators on  is
is  The corresponding spectrum is defined by
The corresponding spectrum is defined by 
We are interested in this paper (Section 2) to the study of the stability problem in Fredholm operators set and semi-Fredholm operators set. In the past few years, a lot of work has been done along these lines, [3–5] and others. A well-known fact is that  is an open set. An important question is to characterize, for a given
is an open set. An important question is to characterize, for a given  , the class of bounded operators
, the class of bounded operators  on
on  , such that
, such that  still belongs to
still belongs to  . Recall that if
. Recall that if  then
then  (see [2, Theorem 16.9] ). More generally, this fact holds true also for
(see [2, Theorem 16.9] ). More generally, this fact holds true also for  a strictly singular operator (see [6, Proposition
a strictly singular operator (see [6, Proposition  .c.
.c. ]). Noncompactness measures provide advanced techniques to obtain current precise results along this line; see for example [7, 8]. By means of the Kuratowski measure, for a given
]). Noncompactness measures provide advanced techniques to obtain current precise results along this line; see for example [7, 8]. By means of the Kuratowski measure, for a given  , we describe in Theorem 2.2 a class of bounded operators
, we describe in Theorem 2.2 a class of bounded operators  on
on  , for which
, for which  . We should notice that, in general, the size of the perturbation depends upon
. We should notice that, in general, the size of the perturbation depends upon  . This key-result permits to prove in Corollary 2.3 some localization results about the essential spectra
. This key-result permits to prove in Corollary 2.3 some localization results about the essential spectra  and
and  of bounded operators on
of bounded operators on  . Next, we investigate the stability in the semi-Browder operators set. In [9], Grabiner proves that
. Next, we investigate the stability in the semi-Browder operators set. In [9], Grabiner proves that  and
and  are closed under commuting perturbation. In [4], Rakočević extends this result to the perturbation classes associated with the sets of semi-Fredholm operators. In Theorem 2.4, by means of the Kuratowski measure, we characteriz for a given
are closed under commuting perturbation. In [4], Rakočević extends this result to the perturbation classes associated with the sets of semi-Fredholm operators. In Theorem 2.4, by means of the Kuratowski measure, we characteriz for a given  , a class of bounded operators
, a class of bounded operators  on
on  , that commute with
, that commute with  , such that
, such that  As the corollary of this theorem we obtain the main result of Grabiner. As the application of the obtained results, we describe the essential spectra of weighted shift operators.
As the corollary of this theorem we obtain the main result of Grabiner. As the application of the obtained results, we describe the essential spectra of weighted shift operators.
In Section 3, we are interested in the study of polynomially compact operators. Consider  For
For  there exists a unique unitary polynomial
there exists a unique unitary polynomial  of least degree such that
of least degree such that  is compact. This polynomial will be called the minimal polynomial of
is compact. This polynomial will be called the minimal polynomial of  In this section, we describe
In this section, we describe  for
for  with compact commutator such that
with compact commutator such that  Next, we show that if there exists an analytic function
Next, we show that if there exists an analytic function  in a neighborhood of
in a neighborhood of  such that
such that  is compact, then
is compact, then  As application, we use the obtained results to investigate the solvability for operator equations in Banach spaces,
As application, we use the obtained results to investigate the solvability for operator equations in Banach spaces,  For
For  we give affirmative answer under several sufficient conditions on
we give affirmative answer under several sufficient conditions on  This result extends the analysis started in [10, 11] and generalizes the result obtained, in case
This result extends the analysis started in [10, 11] and generalizes the result obtained, in case  , in [12, Theorem
, in [12, Theorem  ].
].
2. Some New Properties in Fredholm Theory by Means of the Kuratowski Measure of Noncompactness
In this section, we give some results concerning the classes of Fredholm operators and Browder operators via the concept of measures of noncompactness. General definition can be found in [13]. We write  for the family of all nonempty and bounded subset of
for the family of all nonempty and bounded subset of  . We deal with a specific measure: the Kuratowski measure of noncompactness defined on
. We deal with a specific measure: the Kuratowski measure of noncompactness defined on  as follows (see [14]):
as follows (see [14]):

For  , we define the two nonnegative quantities (see [15]) associated with
, we define the two nonnegative quantities (see [15]) associated with  by
by

Let  be an infinite dimensional subspace of
be an infinite dimensional subspace of  and let
and let  be the natural embedding of
be the natural embedding of  into
into  . The disc (resp., circle) with center
. The disc (resp., circle) with center  and radius
and radius  is denoted by
is denoted by  (resp.,
(resp.,  ). We write
). We write  for the closure of
for the closure of  and we use
and we use  for
for 
We start this section by some fundamental properties satisfied by  and
and  which will be useful in the remainder of the text. For more detail, we refer to [15].
which will be useful in the remainder of the text. For more detail, we refer to [15].
Proposition 2.1.
Let  be in
be in  Then one has the following.
Then one has the following.
(i) and
and  , for all
, for all 
(ii)
(iii) and
and 
(iv)
(v)If  is an isomorphism, then
is an isomorphism, then 
(vi) if and only if
if and only if 
(vii) and
and 
In the following theorem we establish a stability property in the upper semi-Fredholm operators set. This result provides, in particular, an extension of Theorem  in [8].
in [8].
Theorem 2.2.
Let  be two bounded operators on
be two bounded operators on  and let
and let  be an analytic function in a neighborhood
be an analytic function in a neighborhood  of
of  not vanishing on a connected component of
not vanishing on a connected component of  .
.
(i)If  , then
, then  and
and 
Suppose moreover that the commutator  and
and  , then one has the following.
, then one has the following.
(ii)
(iii) implies that
implies that  .
.
(iv) for some
for some  implies that
implies that 
Proof.
By Proposition 2.1, we have for all 
 then
then  for all
for all  in particular,
in particular,  By the continuity of the index on
By the continuity of the index on  , we get
, we get  and this proves (i).
and this proves (i).
Now, assume that  applying (i), we get
applying (i), we get  and
and  Let
Let  be an open set with closure
be an open set with closure  and whose boundary
and whose boundary  consists of finite number of simple closed curves that do not intersect, and such that
consists of finite number of simple closed curves that do not intersect, and such that  . Then we have
. Then we have

Since  then there exist compact operators
then there exist compact operators  and
and  such that
such that

Integrating along  , we get
, we get

where  It is easily checked that
It is easily checked that  and
and  This leads to
This leads to  If
If  then
then  By (2.5), we conclude that
By (2.5), we conclude that 
Now, if  then
then  yields
yields  . Therefore, by (ii)
. Therefore, by (ii) By the continuity of the index function on
By the continuity of the index function on  we get
we get 
For  define
define  (resp.,
(resp.,  ) to be the limit of the sequence
) to be the limit of the sequence  (resp.,
(resp.,  ). For the existence of these limits see [2, Lemma
). For the existence of these limits see [2, Lemma  ].
].
Corollary 2.3.
Let  be a bounded operator on
be a bounded operator on  , the one has the following.
, the one has the following.
(i)
(ii)If  then
then 
(iii)If  then
then 
(iv)If  then
then 
(v)If  then
then 
Proof.
Let  and suppose that
and suppose that  then, by Theorem 2.2(iv), we have
then, by Theorem 2.2(iv), we have  and
and  Hence, if
Hence, if  then
then  and this proves (i).
and this proves (i).
Notice that if  then
then  and the results are all trivial. Suppose that
and the results are all trivial. Suppose that  . For
. For  , there exists
, there exists  such that
such that  Then, by Theorem 2.2(iv), we have
Then, by Theorem 2.2(iv), we have  and
and  Hence, we get easily (ii)–(v).
Hence, we get easily (ii)–(v).
2.1. Stability in the Browder and the Semi-Browder Operators
The following theorem uses the measure of noncompactness to establish stability in the semi-Browder operators set. More precisely, we have the following.
Theorem 2.4.
Suppose that  and
and  are commuting bounded linear operators on the Banach space
are commuting bounded linear operators on the Banach space  Assume that
Assume that  then
then

Proof.
For  we have
we have  and then, by Theorem 2.2(i),
and then, by Theorem 2.2(i),  Set
Set  and
and  Since
Since  and
and  are commuting, then according to [16, Theorem
are commuting, then according to [16, Theorem  ], for all
], for all  there exists
there exists  such that, for all
such that, for all  in the disk
in the disk 

Hence,  is a locally constant function of
is a locally constant function of  on the interval
on the interval  Since every locally constant function on a connected set is constant, then
Since every locally constant function on a connected set is constant, then

Now, since  then from [5, Proposition 1.6(i)]
then from [5, Proposition 1.6(i)]

Thus,  and again by [5, Proposition
and again by [5, Proposition  ], it follows that
], it follows that 
Remark 2.5.
Theorem 2.4 extends the results of Grabiner [9, Theorem  ]. Indeed, if
]. Indeed, if  is compact, we obtain
is compact, we obtain  Hence, Theorem 2.4 yields
Hence, Theorem 2.4 yields  if and only if
if and only if  This proves that
This proves that  is closed under commuting compact perturbation. By duality argument, we prove the closeness of
is closed under commuting compact perturbation. By duality argument, we prove the closeness of 
Corollary 2.6.
Let  be commuting bounded operators on
be commuting bounded operators on  Suppose that there exists
Suppose that there exists  such that
such that 
(i)If  then
then 
(ii)If  then
then 
Proof.
-
(i)
Let
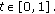 Since
Since 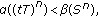 then from Theorem 2.2,
then from Theorem 2.2,  Arguing as in the proof of Theorem 2.4, we get the result.
Arguing as in the proof of Theorem 2.4, we get the result. -
(ii)
Since
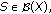 then
then 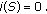 By Theorem 2.2,
By Theorem 2.2, 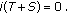 On the other hand, (i) yields
On the other hand, (i) yields  According to [17, Theorem
According to [17, Theorem 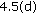 ], we get
], we get 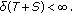
Corollary 2.7.
Let  be a bounded operator on
be a bounded operator on  , thene one has the following.
, thene one has the following.
(i)
(ii)If  then
then 
Proof.
-
(i)
For
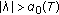 , there exists
, there exists 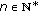 such that
such that 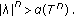 By Corollary 2.6, we have
By Corollary 2.6, we have  . The result follows since we can choose
. The result follows since we can choose  arbitrary large.
arbitrary large. -
(ii)
Since
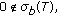 then
then 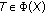 and hence
and hence  For
For 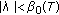 , there exists
, there exists 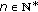 such that
such that 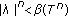 . Corollary 2.6 implies that
. Corollary 2.6 implies that  since
since 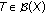 .
.
2.2. Application: Weighted Shift Operators
Let  be a bounded complex sequence. Consider the unilateral backward weighted shift operator
be a bounded complex sequence. Consider the unilateral backward weighted shift operator  defined on
defined on  by
by  In [18, Proposition
In [18, Proposition  ], the authors give a localization results for the spectrum and the approximate point spectrum of unilateral backward weighted shift operator. In this section, we investigate the Wolf essential spectrum of
], the authors give a localization results for the spectrum and the approximate point spectrum of unilateral backward weighted shift operator. In this section, we investigate the Wolf essential spectrum of  .
.
Proposition 2.8.
The following statements hold true.
(i) and
and 
(ii)
Proof.
For  the set
the set  is finite. Consider
is finite. Consider

We have  . Since
. Since  is finite dimensional subspace, then
is finite dimensional subspace, then

Otherwise, by Proposition 2.1,

Since we can choose  arbitrary small, then we get (i).
arbitrary small, then we get (i).
We should notice that if  is a cluster point for the sequence
is a cluster point for the sequence  , then
, then  and (ii) follows from Corollary 2.3(i). If not, then
and (ii) follows from Corollary 2.3(i). If not, then  is a finite set and
is a finite set and  is a Fredholm operator with index
is a Fredholm operator with index  More precisely,
More precisely,  and
and  , here
, here  denotes the cardinal of
denotes the cardinal of  Now, by Corollary 2.3(iii), we get
Now, by Corollary 2.3(iii), we get  , which proves the proposition.
, which proves the proposition.
Remark 2.9.
Notice that if  converges to
converges to  , then according to Proposition 2.8, we get
, then according to Proposition 2.8, we get  and
and  Since
Since  then by the continuity of the index function on
then by the continuity of the index function on  , we obtain
, we obtain  This is a well-known fact (see, e.g., [19, Proposition 27.7, page 139]).
This is a well-known fact (see, e.g., [19, Proposition 27.7, page 139]).
In what follows, we investigate more precisely the essential spectrum of  . For this end define
. For this end define  to be the limit set of
to be the limit set of  , that is, the set of all cluster points of the sequence
, that is, the set of all cluster points of the sequence  , and
, and  to be the limit set of
to be the limit set of  for
for 
Proposition 2.10.
Suppose that  is finite, then
is finite, then

Proof.
For  consider
consider  and
and  We can write
We can write  For
For  define the operator
define the operator  by
by

Since,  and
and  then
then

This yields

Observe that  is finite dimensional and then
is finite dimensional and then  is finite rank. Hence,
is finite rank. Hence,  It remains to prove that,
It remains to prove that,  Consider the operator
Consider the operator  defined by
defined by

where  is the corresponding un-weighted shift operator. We have
is the corresponding un-weighted shift operator. We have  , with
, with  being the sequence defined by
being the sequence defined by

Observe that  converges and
converges and  then
then  Since
Since  then, as above,
then, as above,  Hence,
Hence,  and this completes the proof.
and this completes the proof.
Now, we prove the following result.
Theorem 2.11.
Suppose that there exists  such that
such that  is a finite set, then
is a finite set, then

Proof.
(by induction). For  the result follows by Proposition 2.10. Let
the result follows by Proposition 2.10. Let  be an integer and suppose that if
be an integer and suppose that if  is a finite set, then (2.19) holds true. Suppose now that
is a finite set, then (2.19) holds true. Suppose now that  is a finite set. For
is a finite set. For  and
and  , we consider
, we consider  and
and  Define the sequence
Define the sequence  by
by

Since  and
and  for all
for all  then
then

Observe that  is a finite set and
is a finite set and  Hence
Hence

Now, consider the sequence  defined by
defined by

Clearly,  and
and  Hence, by Proposition 2.8,
Hence, by Proposition 2.8,  Since
Since  and
and  then
then

Hence, we get, for 

Since we can choose  arbitrary small, then by (2.21), (2.22), and (2.25), we get (2.19).
arbitrary small, then by (2.21), (2.22), and (2.25), we get (2.19).
Finally, consider the superposition of two weighted shift operators  Suppose that
Suppose that  then, by Proposition 2.8,
then, by Proposition 2.8,  By Theorem 2.2,
By Theorem 2.2,  and
and 
To close this section, we define a special class of bounded operators on a Banach space  that presents some interesting properties. Set
that presents some interesting properties. Set

First, we observe that  and
and  for all
for all  Also, we notice that if
Also, we notice that if  is a complex sequence that converges, then the weighted shift operator
is a complex sequence that converges, then the weighted shift operator  is a nontrivial element of
is a nontrivial element of  Now, we prove the following result.
Now, we prove the following result.
Proposition 2.12.
(i)For all  one has
one has  and
and 
(ii)If  is invertible, then
is invertible, then 
Proof.
We observe, by Proposition 2.1, that

This proves the statement (i). Again, by Proposition 2.1, for  invertible, we have
invertible, we have  This proves (ii).
This proves (ii).
As an immediate result we get, for all  being in
being in  In the following proposition we describe the essential spectra for a given
In the following proposition we describe the essential spectra for a given 
Proposition 2.13.
Let  be in
be in  and suppose that
and suppose that  then one has the following.
then one has the following.
(i)
(ii)If  then
then 
(iii)If  then
then 
Proof.
According to Corollary 2.3, we have  By Corollary 2.7, we get
By Corollary 2.7, we get  . Since
. Since  , then we get (i). The assertion (ii) follows from Corollary 2.3(i)–(ii). For (iii), on one hand, by Corollary 2.3(iii), we have
, then we get (i). The assertion (ii) follows from Corollary 2.3(i)–(ii). For (iii), on one hand, by Corollary 2.3(iii), we have  on the other hand, the boundary
on the other hand, the boundary 
Notice that if  is a complex sequence that converges to
is a complex sequence that converges to  , then by Proposition 2.13 (i),
, then by Proposition 2.13 (i),

3. Fredholm Theory for Polynomially Compact Operators
In this section, we present a spectral analysis for polynomially compact operators. We begin by proving an important result about perturbation by polynomially compact operators in the general context of normed spaces. First, we make the following definition.
Definition 3.1.
Let  be a normed space, let
be a normed space, let 
 be the minimal polynomial of
be the minimal polynomial of  and let
and let  We say that
We say that  and
and  communicate if There exists a continuous map
communicate if There exists a continuous map  and
and  such that, for all
such that, for all  zero of
zero of 
Theorem 3.2.
Let  be two bounded operators on a normed space
be two bounded operators on a normed space  with compact commutator. Suppose that
with compact commutator. Suppose that  and
and  for all
for all  Then
Then 
If moreover,  and
and  communicate, then
communicate, then 
Proof.
Since  for all
for all  then we can write
then we can write  with
with  This yields
This yields  On the other hand
On the other hand  is compact, then
is compact, then  Writing
Writing  with
with  and
and  we conclude that
we conclude that 
Now, consider  then
then  Thus,
Thus,  is compact and, for all
is compact and, for all  This yields
This yields

By the continuity of the index function on  we get
we get  constant for all
constant for all  . In particular,
. In particular, 
Remark 3.3.
Theorem 3.2 is an improvement of [12, Theorem  ]. Indeed, if
]. Indeed, if  is a discrete set of
is a discrete set of  then
then  and
and  communicate. In the particular case where
communicate. In the particular case where  we have
we have  . Therefore,
. Therefore,  is a Fredholm operator of index zero.
is a Fredholm operator of index zero.
We notice that if, for some  then, for all
then, for all  and
and  communicate. Hence, we obtain the following.
communicate. Hence, we obtain the following.
Corollary 3.4.
Let  be two bounded operators on a normed space
be two bounded operators on a normed space  with compact commutator. Suppose that
with compact commutator. Suppose that  for some
for some  If
If  then
then  and
and 
Corollary 3.5.
Let  be two commuting bounded operators on the Banach space
be two commuting bounded operators on the Banach space  . Suppose that
. Suppose that  ,
,  and assume that
and assume that  and
and  communicate, then
communicate, then 
Proof.
As in the proof of Theorem 3.2, (3.1) we obtain  Arguing as in the proof of Theorem 2.4, we get
Arguing as in the proof of Theorem 2.4, we get  . Now, by Theorem 3.2, we have
. Now, by Theorem 3.2, we have  Therefore, according to [17, Theorem
Therefore, according to [17, Theorem  ] we get
] we get 
The following proposition is a well-know result, see [12, 20]. Here, we present a simple proof for this fact.
Proposition 3.6.
Let  and let
and let  be the minimal polynomial of
be the minimal polynomial of  Then
Then

Proof.
Since  is compact, then
is compact, then  By [3, Theorem
By [3, Theorem  ],
],  Hence,
Hence,  Let
Let  be such that
be such that  we can write
we can write  Since
Since  is compact and, by the minimality of
is compact and, by the minimality of  ,
,  is not compact, then
is not compact, then  . Hence,
. Hence, 
Proposition 3.7.
Let  be two bounded operators on
be two bounded operators on  with compact commutator.
with compact commutator.
(i)
(ii)If there exists  such that
such that  then
then 
Proof.
-
(i)
If
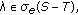 then
then  On the other hand
On the other hand  and
and 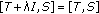 is compact. According to Theorem 3.2, there exists
is compact. According to Theorem 3.2, there exists 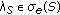 such that
such that  where
where 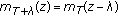 is the minimal polynomial of
is the minimal polynomial of 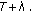 Hence
Hence 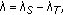 where
where 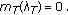 Finally, the result follows from Proposition 3.6
Finally, the result follows from Proposition 3.6 -
(ii)
By (i),
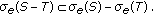 Since
Since 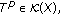 then
then  and we obtain
and we obtain 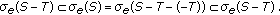
Notice that in general, the converse inclusion in (i) does not hold.
Example 3.8.
Consider the unweighted shift operator  According to Remark 2.9, we have
According to Remark 2.9, we have  the unit circle. Let
the unit circle. Let  be a bounded complex sequence and let
be a bounded complex sequence and let  be defined by
be defined by  Suppose that
Suppose that  then
then  Consider
Consider  then
then  Suppose that
Suppose that  then, applying Theorem 3.2, we get that
then, applying Theorem 3.2, we get that  is a Fredholm operator. By Proposition 3.7, we get
is a Fredholm operator. By Proposition 3.7, we get 
The index of  depends on the position of
depends on the position of  with respect to
with respect to  If
If  then
then  and
and  communicate and by Theorem 3.2,
communicate and by Theorem 3.2,  If we suppose that
If we suppose that  with
with  then
then  and
and  is invertible. In this case
is invertible. In this case  Observe that in this case,
Observe that in this case,  and
and  do not communicate.
do not communicate.
Theorem 3.9.
Let  be a bounded operator on
be a bounded operator on  Suppose that there exists an analytic function
Suppose that there exists an analytic function  in a neighborhood of
in a neighborhood of  which does not vanish on a connected component of
which does not vanish on a connected component of  such that
such that  then
then 
Proof.
From [3, Theorem  ] , we have
] , we have  Since
Since  then
then  Hence,
Hence,  and therefore,
and therefore,  is a finite set
is a finite set  . Write
. Write  where
where  and
and  is an analytic function with
is an analytic function with  Since
Since  does not vanish on
does not vanish on  then
then  Thus,
Thus,  and
and 
3.1. Application: Solvability of Operator Equations
In the following theorem, we treat the question of the solvability of operator equations. We will prove, under several sufficient conditions, that if the homogeneous equation  only has the trivial solution
only has the trivial solution  then for all
then for all  the nonhomogeneous equation
the nonhomogeneous equation  has a unique solution
has a unique solution  , and this solution depends continuously on
, and this solution depends continuously on 
Theorem 3.10.
Let  be a normed space and let
be a normed space and let  be two communicating commuting bounded operators on
be two communicating commuting bounded operators on  . Suppose that
. Suppose that  and let
and let  be the minimal polynomial of
be the minimal polynomial of  Assume that
Assume that 
If  is injective, then the inverse operator
is injective, then the inverse operator  exists and is bounded.
exists and is bounded.
Proof.

is injective, then  thus
thus  Applying Theorem 3.2, we get
Applying Theorem 3.2, we get  It follows that
It follows that  and therefore, the operator
and therefore, the operator  is surjective. Hence, the inverse operator
is surjective. Hence, the inverse operator  exists. Since
exists. Since  is not necessary a Banach space, we have to prove that
is not necessary a Banach space, we have to prove that  is bounded. Suppose that it is not so, then there exists
is bounded. Suppose that it is not so, then there exists  with
with  and the sequence
and the sequence  satisfies:
satisfies:  as
as  Set
Set  Then
Then  as
as  and
and  Since
Since  and
and  then there exists
then there exists  such that
such that

Since  is compact, we can choose a subsequence
is compact, we can choose a subsequence  such that
such that  as
as  Using (3.3), we observe that
Using (3.3), we observe that  as
as  On the one hand,
On the one hand,  as
as  On the other hand,
On the other hand,  Hence,
Hence,  which implies that
which implies that  This is in contradiction with
This is in contradiction with 
Theorem 3.11.
Let  and
and  be communicating, commuting operators on the Banach space
be communicating, commuting operators on the Banach space  . Suppose that
. Suppose that  and set
and set  . Then the projection
. Then the projection  defined by the decomposition
defined by the decomposition  is compact, and the operator
is compact, and the operator  is bijective.
is bijective.
Proof.
First we notice that by Corollary 3.5,  , then
, then  and
and  . Thus,
. Thus,  which implies that
which implies that  is finite dimensional. Hence, the projection
is finite dimensional. Hence, the projection  is continuous and compact. Now, we claim that
is continuous and compact. Now, we claim that  is bijective. Let
is bijective. Let  Since
Since  then
then  which implies that
which implies that  Thus
Thus  Since
Since  then
then  We get by iteration
We get by iteration  On the other hand, from Theorem 3.10 applied to the operator
On the other hand, from Theorem 3.10 applied to the operator  we conclude that
we conclude that  is surjective.
is surjective.
References
Caradus SR, Pfaffenberger WE, Yood B: Calkin Algebras and Algebras of Operators on Banach Spaces. Marcel Dekker, New York, NY, USA; 1974.
Müller V: Spectral Theory of Linear Operators and Spectral Systems in Banach Algebras. Birkhäuser, Basel, Switzerland; 2007.
Nussbaum RD: Spectral mapping theorems and perturbation theorems for Browder's essential spectrum. Transactions of the American Mathematical Society 1970, 150: 445–455.
Rakočević V: Semi-Fredholm operators with finite ascent or descent and perturbations. Proceedings of the American Mathematical Society 1995,123(12):3823–3825.
West TT: A Riesz-Schauder theorem for semi-Fredholm operators. Proceedings of the Royal Irish Academy. Section A 1987,87(2):137–146.
Lindenstrauss J, Tzafriri L: Classical Banach Spaces I. Springer, Berlin, Germany; 1996.
Abdelmoumen B, Dehici A, Jeribi A, Mnif M: Some new properties in Fredholm theory, Schechter essential spectrum, and application to transport theory. Journal of Inequalities and Applications 2008, 2008:-14.
Lebow A, Schechter M: Semigroups of operators and measures of noncompactness. Journal of Functional Analysis 1971, 7: 1–26. 10.1016/0022-1236(71)90041-3
Grabiner S: Ascent, descent and compact perturbations. Proceedings of the American Mathematical Society 1978,71(1):79–80. 10.1090/S0002-9939-1978-0495841-7
Fredholm I: Sur une classe d'équations fonctionnelles. Acta Mathematica 1903,27(1):365–390. 10.1007/BF02421317
Riesz F: Über lineare funktionalgleichungen. Acta Mathematica 1918, 47: 71–98.
Jeribi A, Moalla N: Fredholm operators and Riesz theory for polynomially compact operators. Acta Applicandae Mathematicae 2006,90(3):227–247. 10.1007/s10440-006-9023-8
Banaś J, Geobel K: Measures of Noncompactness in Banach Spaces, Lecture Notes in Pure and Applied Mathematics. Volume 60. Marcel Dekker, New York, NY, USA; 1980.
Darbo G: Punti uniti in trasformazioni a codominio non compatto. Rendiconti del Seminario Matematico della Università di Padova 1955, 24: 84–92.
Furi M, Martelli M, Vignoli A: Contributions to the spectral theory for nonlinear operators in Banach spaces. Annali di Matematica Pura ed Applicata 1978,118(1):229–294. 10.1007/BF02415132
Goldmann MA, Kračkovskiĭ SN: Behavior of the space of zeros with a finite-dimensional salient on the Riesz kernel under perturbations of the operator. Doklady Akademii Nauk SSSR 1975,221(13):532–534. English translation in Soviet Mathematics—Doklady, vol. 16, pp. 370–373, 1975 English translation in Soviet Mathematics—Doklady, vol. 16, pp. 370–373, 1975
Taylor AE: Theorems on ascent, descent, nullity and defect of linear operators. Mathematische Annalen 1966, 163: 18–49. 10.1007/BF02052483
Laursen KB, Neumann M: An Introduction to Local Spectral Theory. , London, UK; 2000.
Conway JB: A Course in Operator Theory. American Mathematical Society, Providence, RI, USA; 1999.
Gilfeather F: The structure and asymptotic behavior of polynomially compact operators. Proceedings of the American Mathematical Society 1970, 25: 127–134. 10.1090/S0002-9939-1970-0257791-3
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Abdelmoumen, B., Baklouti, H. Perturbation Results on Semi-Fredholm Operators and Applications. J Inequal Appl 2009, 284526 (2009). https://doi.org/10.1155/2009/284526
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/284526
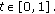 Since
Since 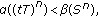 then from Theorem 2.2,
then from Theorem 2.2,  Arguing as in the proof of Theorem 2.4, we get the result.
Arguing as in the proof of Theorem 2.4, we get the result.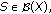 then
then 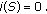 By Theorem 2.2,
By Theorem 2.2, 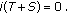 On the other hand, (i) yields
On the other hand, (i) yields  According to [
According to [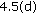 ], we get
], we get 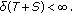
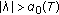 , there exists
, there exists 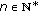 such that
such that 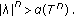 By Corollary 2.6, we have
By Corollary 2.6, we have  . The result follows since we can choose
. The result follows since we can choose  arbitrary large.
arbitrary large.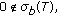 then
then 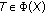 and hence
and hence  For
For 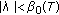 , there exists
, there exists 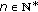 such that
such that 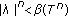 . Corollary 2.6 implies that
. Corollary 2.6 implies that  since
since 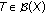 .
.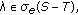 then
then  On the other hand
On the other hand  and
and 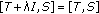 is compact. According to Theorem 3.2, there exists
is compact. According to Theorem 3.2, there exists 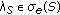 such that
such that  where
where 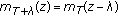 is the minimal polynomial of
is the minimal polynomial of 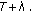 Hence
Hence 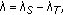 where
where 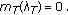 Finally, the result follows from Proposition 3.6
Finally, the result follows from Proposition 3.6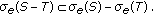 Since
Since 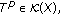 then
then  and we obtain
and we obtain