- Research Article
- Open access
- Published:
On The Hadamard's Inequality for Log-Convex Functions on the Coordinates
Journal of Inequalities and Applications volume 2009, Article number: 283147 (2009)
Abstract
Inequalities of the Hadamard and Jensen types for coordinated log-convex functions defined in a rectangle from the plane and other related results are given.
1. Introduction
Let  be a convex mapping defined on the interval
be a convex mapping defined on the interval  of real numbers and
of real numbers and  , with
, with  , then
, then

holds, this inequality is known as the Hermite-Hadamard inequality. For refinements, counterparts, generalizations and new Hadamard-type inequalities, see [1–8].
A positive function  is called log-convex on a real interval
is called log-convex on a real interval  , if for all
, if for all  and
and  ,
,

If  is a positive log-concave function, then the inequality is reversed. Equivalently, a function
is a positive log-concave function, then the inequality is reversed. Equivalently, a function  is log-convex on
is log-convex on  if
if  is positive and
is positive and  is convex on
is convex on  . Also, if
. Also, if  and
and  exists on
exists on  , then
, then  is log-convex if and only if
is log-convex if and only if  .
.
The logarithmic mean of the positive real numbers  ,
,  , is defined as
, is defined as

A version of Hadamard's inequality for log-convex (concave) functions was given in [9], as follows.
Theorem 1.1.
Suppose that  is a positive log-convex function on
is a positive log-convex function on  , then
, then

If  is a positive log-concave function, then the inequality is reversed.
is a positive log-concave function, then the inequality is reversed.
For refinements, counterparts and generalizations of log-convexity see [9–13].
A convex function on the coordinates was introduced by Dragomir in [8]. A function  which is convex in
which is convex in  is called coordinated convex on
is called coordinated convex on  if the partial mapping
if the partial mapping  ,
,  and
and  ,
,  , are convex for all
, are convex for all  and
and  .
.
An inequality of Hadamard's type for coordinated convex mapping on a rectangle from the plane  established by Dragomir in [8], is as follows.
established by Dragomir in [8], is as follows.
Theorem 1.2.
Suppose that  is coordinated convex on
is coordinated convex on  , then
, then

The above inequalities are sharp.
The maximum modulus principle in complex analysis states that if  is a holomorphic function, then the modulus
is a holomorphic function, then the modulus  cannot exhibit a true local maximum that is properly within the domain of
cannot exhibit a true local maximum that is properly within the domain of  . Characterizations of the maximum principle for sub(super)harmonic functions are considered in [14], as follows.
. Characterizations of the maximum principle for sub(super)harmonic functions are considered in [14], as follows.
Theorem 1.3.
Let  be a region and let
be a region and let  be a sub(super)harmonic function. If there is a point
be a sub(super)harmonic function. If there is a point  with
with  , for all
, for all  then
then  is a constant function.
is a constant function.
Theorem 1.4.
Let  be a region and let
be a region and let  and
and  be bounded real-valued functions defined on
be bounded real-valued functions defined on  such that
such that  is subharmonic and
is subharmonic and  is superharmonic. If for each point
is superharmonic. If for each point 

then  for all
for all  or
or  and
and  is harmonic.
is harmonic.
In this paper, a new version of the maximum (minimum) principle in terms of convexity, and some inequalities of the Hadamard type are obtained.
2. On Coordinated Convexity and Sub(Super)Harmonic Functions
Consider the  -dimensional interval
-dimensional interval  in
in  . A function
. A function  is called convex in
is called convex in  if
if

holds for all  and
and  .
.
As in [8], we define a log-convex function on the coordinates as follows: a function  will be called coordinated log-convex on
will be called coordinated log-convex on  if the partial mappings
if the partial mappings  ,
,  and
and  ,
,  , are log-convex for all
, are log-convex for all  and
and  . A formal definition of a coordinated log-convex function may be stated as follows.
. A formal definition of a coordinated log-convex function may be stated as follows.
Definition 2.1.
A function  will be called coordinated log-convex on
will be called coordinated log-convex on  , for all
, for all  and
and  , if the following inequality holds,
, if the following inequality holds,

Equivalently, we can determine whether or not the function  is coordinated log-convex by using the following lemma.
is coordinated log-convex by using the following lemma.
Lemma 2.2.
Let  . If
. If  is twice differentiable then
is twice differentiable then  is coordinated log-convex on
is coordinated log-convex on  if and only if for the functions
if and only if for the functions  , defined by
, defined by  and
and  , defined by
, defined by  , we have
, we have

Proof.
The proof is straight forward using the elementary properties of log-convexity in one variable.
Proposition 2.3.
Suppose that  is twice differentiable on
is twice differentiable on  and log-convex on
and log-convex on  and
and  is twice differentiable on
is twice differentiable on  and log-convex on
and log-convex on  . Let
. Let  be a twice differentiable function defined by
be a twice differentiable function defined by  , then
, then  is coordinated log-convex on
is coordinated log-convex on  .
.
Proof.
This follows directly using Lemma 2.2.
The following result holds.
Proposition 2.4.
Every log-convex function  is log-convex on the coordinates, but the converse is not generally true.
is log-convex on the coordinates, but the converse is not generally true.
Proof.
Suppose that  is convex in
is convex in  . Consider the function
. Consider the function  ,
,  , then for
, then for  , and
, and  , we have
, we have

which shows the log-convexity of  . The proof that
. The proof that  ,
,  , is also log-convex on
, is also log-convex on  for all
for all  follows likewise. Now, consider the mapping
follows likewise. Now, consider the mapping  given by
given by  . It is obvious that
. It is obvious that  is log-convex on the coordinates but not log-convex on
is log-convex on the coordinates but not log-convex on  . Indeed, if
. Indeed, if  and
and  , we have:
, we have:

Thus, for all  and
and  , we have
, we have

which shows that  is not log-convex on
is not log-convex on  .
.
In the following, a Jensen-type inequality for coordinated log-convex functions is considered.
Proposition 2.5.
Let  be a positive coordinated log-convex function on the open set
be a positive coordinated log-convex function on the open set  and let
and let  ,
,  . If
. If  and
and  ,
,  , then
, then

Proof.
Let  ,
,  be such that
be such that  , and let
, and let  ,
,  be such that
be such that  , then we have,
, then we have,

and, since  is positive,
is positive,

which is as required.
Remark 2.6.
Let  , then the following inequality holds:
, then the following inequality holds:

The above result may be generalized to the integral form as follows.
Proposition 2.7.
Let  be a positive coordinated log-convex function on the
be a positive coordinated log-convex function on the  and let
and let  be integrable with
be integrable with  , and let
, and let  be integrable with
be integrable with  . If
. If  is positive,
is positive,  , and
, and  is integrable on
is integrable on  and
and  is positive,
is positive,  , and
, and  is integrable on
is integrable on  then
then

Proof.
Applying Jensen's integral inequality in one variable on the  -coordinate and on the
-coordinate and on the  -coordinate we get the required result. The details are omitted.
-coordinate we get the required result. The details are omitted.
Theorem 2.8.
Let  be a positive coordinated log-convex function in
be a positive coordinated log-convex function in  , then for all distinct
, then for all distinct  , such that
, such that  and distinct
and distinct  such that
such that  , the following inequality holds:
, the following inequality holds:

Proof.
Let  be distinct points in
be distinct points in  and let
and let  be distinct points in
be distinct points in  . Setting
. Setting  ,
,  and let
and let  ,
,  , we have
, we have

and we can write

From this inequality it is easy to deduce the required result (2.12).
The subharmonic functions exhibit many properties of convex functions. Next, we give some results for the coordinated convexity and sub(super)harmonic functions.
Proposition 2.9.
Let  be coordinated convex (concave) on
be coordinated convex (concave) on  . If
. If  is a twice differentiable on
is a twice differentiable on  , then
, then  is sub(super)harmonic on
is sub(super)harmonic on  .
.
Proof.
Since  is coordinated convex on
is coordinated convex on  then the partial mappings
then the partial mappings  ,
,  and
and  ,
,  , are convex for all
, are convex for all  and
and  . Equivalently, since
. Equivalently, since  is differentiable we can write
is differentiable we can write

for all  , and
, and

for all  , which imply that
, which imply that

which shows that  is subharmonic. If
is subharmonic. If  is coordinated concave on
is coordinated concave on  , replace "
, replace " '' by "
'' by " '' above, we get that
'' above, we get that  is superharmonic on
is superharmonic on  .
.
We now give two version(s) of the Maximum (Minimum) Principle theorem using convexity on the coordinates.
Theorem 2.10.
Let  be a coordinated convex (concave) function on
be a coordinated convex (concave) function on  . If
. If  is twice differentiable in
is twice differentiable in  and there is a point
and there is a point  with
with  , for all
, for all  then
then  is a constant function.
is a constant function.
Proof.
By Proposition 2.9, we get that  is sub(super)harmonic. Therefore, by Theorem 1.3 and the maximum principal the required result holds (see [14, page 264]).
is sub(super)harmonic. Therefore, by Theorem 1.3 and the maximum principal the required result holds (see [14, page 264]).
Theorem 2.11.
Let  and
and  be two twice differentiable functions in
be two twice differentiable functions in  . Assume that
. Assume that  and
and  are bounded real-valued functions defined on
are bounded real-valued functions defined on  such that
such that  is coordinated convex and
is coordinated convex and  is coordinated concave. If for each point
is coordinated concave. If for each point 

then  for all
for all  or
or  and
and  is harmonic.
is harmonic.
Proof.
By Proposition 2.9, we get that  is subharmonic and
is subharmonic and  is superharmonic. Therefore, by Theorem 1.4 and using the maximum principal the required result holds, (see [14, page 264]).
is superharmonic. Therefore, by Theorem 1.4 and using the maximum principal the required result holds, (see [14, page 264]).
Remark 2.12.
The above two results hold for log-convex functions on the coordinates, simply, replacing  by
by  , to obtain the results.
, to obtain the results.
3. Some Inequalities and Applications
In the following we develop a Hadamard-type inequality for coordinated log-convex functions.
Corollary 3.1.
Suppose that  is log-convex on the coordinates of
is log-convex on the coordinates of  , then
, then

For a positive coordinated log-concave function  , the inequalities are reversed.
, the inequalities are reversed.
Proof.
In Theorem 1.2, replace  by
by  and we get the required result.
and we get the required result.
Lemma 3.2.
For  with
with  , the function
, the function

is convex for all  . Moreover,
. Moreover,

for all  .
.
Proof.
Since  is twice differentiable for all
is twice differentiable for all  with
with  , we note that for all
, we note that for all  ,
,  , which shows that
, which shows that  is increasing and thus
is increasing and thus  is nonnegative which is equivalent to saying that
is nonnegative which is equivalent to saying that  is increasing and hence
is increasing and hence  is convex. Now, using inequality (1.1), we get
is convex. Now, using inequality (1.1), we get

which completes the proof.
Theorem 3.3.
Suppose that  is log-convex on the coordinates of
is log-convex on the coordinates of  . Let
. Let

then the inequalities

hold, where  is the Euler constant,
is the Euler constant,

is the exponential integral function. For a coordinated log-concave function  , the inequalities are reversed.
, the inequalities are reversed.
Proof.
Since  is log-convex on the coordinates of
is log-convex on the coordinates of  , then
, then

Integrating the previous inequality with respect to  and
and  on
on  , we have,
, we have,

Therefore, by (3.9) and for nonzero, positive  , we have the following cases.
, we have the following cases.
(1)If  , the result is trivial.
, the result is trivial.
(2)If  , then
, then

-
(3)
If
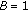 , then
, then  (3.11)
(3.11)
-
(4)
If
 , then
, then 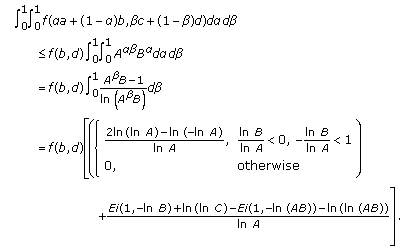 (3.12)
(3.12)
-
(5)
If
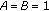 , then
, then  (3.13)
(3.13)
-
(6)
If
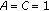 , then
, then 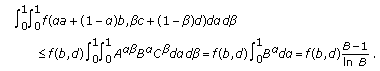 (3.14)
(3.14)
-
(7)
If
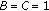 , then
, then 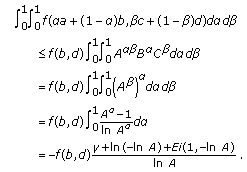 (3.15)
(3.15)
-
(8)
If
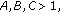 then
then 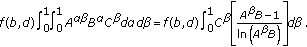 (3.16)
(3.16)
Therefore, by Lemma 3.2, we deduce that

-
(9)
If
 , we have
, we have

which is difficult to evaluate because it depends on the values of  and
and  .
.
Remark 3.4.
The integrals in (3), (4), and (7) in the proof of Theorem 2.11 are evaluated using Maple Software.
Corollary 3.5.
In Theorem 3.3, if
(1) , then
, then

and for instance, if  ,
,  we deduce
we deduce

(2) , then
, then

and for instance, if  , ?
, ?  , we deduce
, we deduce

Proof.
Follows directly by applying inequality (1.4).
References
Dragomir SS: Two mappings in connection to Hadamard's inequalities. Journal of Mathematical Analysis and Applications 1992,167(1):49–56. 10.1016/0022-247X(92)90233-4
Dragomir SS, Agarwal RP: Two inequalities for differentiable mappings and applications to special means of real numbers and to trapezoidal formula. Applied Mathematics Letters 1998,11(5):91–95. 10.1016/S0893-9659(98)00086-X
Dragomir SS, Cho YJ, Kim SS: Inequalities of Hadamard's type for Lipschitzian mappings and their applications. Journal of Mathematical Analysis and Applications 2000,245(2):489–501. 10.1006/jmaa.2000.6769
Dragomir SS, Pearce CEM: Selected Topics on Hermite-Hadamard Inequalities and Applications, RGMIA Monographs. Victoria University, Melbourne City, Australia; 2000.
Dragomir SS, Wang S: A new inequality of Ostrowski's type in norm and applications to some special means and to some numerical quadrature rules. Tamkang Journal of Mathematics 1997,28(3):239–244.
Dragomir SS, Wang S: Applications of Ostrowski's inequality to the estimation of error bounds for some special means and for some numerical quadrature rules. Applied Mathematics Letters 1998,11(1):105–109. 10.1016/S0893-9659(97)00142-0
Dragomir SS, Pearce CEM: Selected Topics on Hermite-Hadamard Inequalities and Applications. RGMIA Monographs, Victoria University, 2000, http://www.staff.vu.edu.au/RGMIA/monographs/hermite_hadamard.html.
Dragomir SS: On the Hadamard's inequality for convex functions on the co-ordinates in a rectangle from the plane. Taiwanese Journal of Mathematics 2001,5(4):775–788.
Gill PM, Pearce CEM, Pecaric J: Hadamard's inequality for -convex functions. Journal of Mathematical Analysis and Applications 1997,215(2):461–470. 10.1006/jmaa.1997.5645
Fink AM: Hadamard's inequality for log-concave functions. Mathematical and Computer Modelling 2000,32(5–6):625–629. 10.1016/S0895-7177(00)00159-X
Pachpatte BG: A note on integral inequalities involving two log-convex functions. Mathematical Inequalities & Applications 2004,7(4):511–515.
Pecaric J, Rehman AU: On logarithmic convexity for power sums and related results. Journal of Inequalities and Applications 2008, 2008:-9.
Qi F: A class of logarithmically completely monotonic functions and application to the best bounds in the second Gautschi-Kershaw's inequality. Journal of Computational and Applied Mathematics 2009,224(2):538–543. 10.1016/j.cam.2008.05.030
Conway JB: Functions of One Complex Variable. I. 7th edition. Springer, New York, NY, USA; 1995.
Acknowledgment
The authors acknowledge the financial support of the Faculty of Science and Technology, Universiti Kebangsaan Malaysia (UKM–GUP–TMK–07–02–107).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Alomari, M., Darus, M. On The Hadamard's Inequality for Log-Convex Functions on the Coordinates. J Inequal Appl 2009, 283147 (2009). https://doi.org/10.1155/2009/283147
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/283147
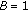 , then
, then 
 , then
, then 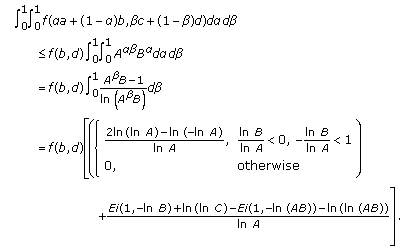
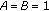 , then
, then 
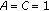 , then
, then 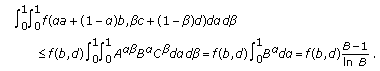
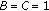 , then
, then 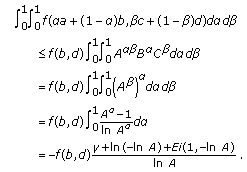
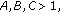 then
then 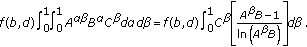
 , we have
, we have