- Research Article
- Open access
- Published:
Moment Inequalities and Complete Moment Convergence
Journal of Inequalities and Applications volume 2009, Article number: 271265 (2009)
Abstract
Let  and
and  be sequences of random variables. For any
be sequences of random variables. For any  and
and  , bounds for
, bounds for  and
and  are obtained. From these results, we establish general methods for obtaining the complete moment convergence. The results of Chow (1988), Zhu (2007), and Wu and Zhu (2009) are generalized and extended from independent (or dependent) random variables to random variables satisfying some mild conditions. Some applications to dependent random variables are discussed.
are obtained. From these results, we establish general methods for obtaining the complete moment convergence. The results of Chow (1988), Zhu (2007), and Wu and Zhu (2009) are generalized and extended from independent (or dependent) random variables to random variables satisfying some mild conditions. Some applications to dependent random variables are discussed.
1. Introduction
Let  be a sequence of random variables defined on a fixed probability space
be a sequence of random variables defined on a fixed probability space  . The most interesting inequalities to probability theory are probably Marcinkiewicz-Zygmund and Rosenthal inequalities. For a sequence
. The most interesting inequalities to probability theory are probably Marcinkiewicz-Zygmund and Rosenthal inequalities. For a sequence  of i.i.d. random variables with
of i.i.d. random variables with  for some
for some  , Marcinkiewicz and Zygmund [1] and Rosenthal [2] (
, Marcinkiewicz and Zygmund [1] and Rosenthal [2] ( and
and  , resp.) proved that there exist positive constants
, resp.) proved that there exist positive constants  and
and  depending only on
depending only on  such that
such that


The following Marcinkiewicz-Zygmund and Rosenthal type maximal inequalities are well known. For a sequence  of i.i.d. random variables with
of i.i.d. random variables with  for some
for some  , there exist positive constants
, there exist positive constants  and
and  depending only on
depending only on  such that
such that


Note that (1.3) and (1.4) imply (1.1) and (1.2), respectively. The above inequalities have been obtained for dependent random variables by many authors. Shao [3] proved that (1.3) and (1.4) hold for negatively associated random variables. Asadian et al. [4] proved that (1.1) and (1.2) hold for negatively orthant dependent random variables.
For a sequence of some mixing random variables, (1.4) holds. However, the constant  depends on both
depends on both  and the sequence of mixing random variables. Shao [5] obtained (1.4) for
and the sequence of mixing random variables. Shao [5] obtained (1.4) for  -mixing identically distributed random variables satisfying
-mixing identically distributed random variables satisfying  . Shao [6] also obtained (1.4) for
. Shao [6] also obtained (1.4) for  -mixing identically distributed random variables satisfying
-mixing identically distributed random variables satisfying  . Utev and Peligrad [7] obtained (1.4) for
. Utev and Peligrad [7] obtained (1.4) for  -mixing random variables.
-mixing random variables.
The concept of complete convergence was introduced by Hsu and Robbins [8]. A sequence  of random variables is said to converge completely to the constant
of random variables is said to converge completely to the constant  if
if

In view of the Borel-Cantelli lemma, this implies that  almost surely. Therefore the complete convergence is a very important tool in establishing almost sure convergence of summation of random variables. Hsu and Robbins [8] proved that the sequence of arithmetic means of i.i.d. random variables converges completely to the expected value if the variance of the summands is finite. Erdös [9] proved the converse.
almost surely. Therefore the complete convergence is a very important tool in establishing almost sure convergence of summation of random variables. Hsu and Robbins [8] proved that the sequence of arithmetic means of i.i.d. random variables converges completely to the expected value if the variance of the summands is finite. Erdös [9] proved the converse.
The result of Hsu-Robbins-Erdös has been generalized and extended in several directions. Baum and Katz [10] proved that if  is a sequence of i.i.d. random variables with
is a sequence of i.i.d. random variables with  ,
,  is equivalent to
is equivalent to

Chow [11] generalized the result of Baum and Katz [10] by showing the following complete moment convergence. If  is a sequence of i.i.d. random variables with
is a sequence of i.i.d. random variables with  for some
for some  and
and  , then
, then

where  . Note that (1.7) implies (1.6) (see Remark 2.6).
. Note that (1.7) implies (1.6) (see Remark 2.6).
Recently, Zhu [12] obtained a complete convergence for  -mixing random variables. Wu and Zhu [13] obtained complete moment convergence results for negatively orthant dependent random variables.
-mixing random variables. Wu and Zhu [13] obtained complete moment convergence results for negatively orthant dependent random variables.
In this paper, we give general methods for obtaining the complete moment convergence by using some moment inequalities. From these results, we generalize and extend the results of Chow [11], Zhu [12], and Wu and Zhu [13] from independent (or dependent) random variables to random variables satisfying some conditions similar to (1.1)–(1.4).
2. Complete Moment Convergence for Random Variables
In this section, we give general methods for obtaining the complete moment convergence by using some moment inequalities. The first two lemmas are simple inequalities for real numbers.
Lemma 2.1.
For any real numbers  ,
,  ,
,  , the inequality holds
, the inequality holds

Proof.
The result follows by an elementary calculation.
The following lemma is a slight generalization of Lemma 2.1.
Lemma 2.2.
Let  and
and  be two sequences of real numbers. Then for any real number
be two sequences of real numbers. Then for any real number  , the inequality holds
, the inequality holds

Proof.
By Lemma 2.1, we obtain

The next two lemmas play essential roles in the paper. Lemma 2.3 gives a moment inequality for the sum of random variables.
Lemma 2.3.
Let  and
and  be sequences of random variables. Then for any
be sequences of random variables. Then for any  ,
,  ,
,  ,
,

Proof.
By Lemma 2.1,

On the other hand, we have by Markov's inequality that

Substituting (2.6) into (2.5), we have the result.
The following lemma gives a moment inequality for the maximum partial sum of random variables.
Lemma 2.4.
Let  and
and  be sequences of random variables. Then for any
be sequences of random variables. Then for any  ,
,  ,
,  ,
,

Proof.
By Lemma 2.2,

The rest of the proof is similar to that of Lemma 2.3 and is omitted.
Now we state and prove one of our main results. The following theorem gives a general method for obtaining the complete moment convergence for sums of random variables satisfying (2.9). The condition (2.9) is well known Marcinkiewicz-Zygmund inequality.
Theorem 2.5.
Let  be an array of random variables with
be an array of random variables with  for
for  ,
,  . Let
. Let  and
and  be sequences of positive real numbers. Suppose that the following conditions hold.
be sequences of positive real numbers. Suppose that the following conditions hold.
(i)For some  , there exists a positive constant
, there exists a positive constant  depending only on
depending only on  such that
such that

where  .
.
(ii) .
.
(iii) .
.
Then

Proof.
Observe that


Then we have by Lemma 2.3, (2.9), (2.11), and (2.12) that

The above two series converge by (ii) and (iii). Hence the result is proved.
Remark 2.6.
If (2.10) holds, then  for all
for all  , since
, since

Hence complete moment convergence is more general than complete convergence.
When  , we have the following theorem. Condition (2.15) is well-known Rosenthal inequality.
, we have the following theorem. Condition (2.15) is well-known Rosenthal inequality.
Theorem 2.7.
Let  be an array of random variables with
be an array of random variables with  for
for  ,
,  . Let
. Let  and
and  be sequences of positive real numbers. Suppose that the following conditions hold.
be sequences of positive real numbers. Suppose that the following conditions hold.
(i)For some  , there exists a positive constant
, there exists a positive constant  depending only on
depending only on  such that
such that

where  .
.
(ii) .
.
(iii) .
.
(iv) for some
for some  .
.
Then (2.10) holds.
Proof.
The proof is same as that of Theorem 2.5 except that

Corollary 2.8.
Let  be a sequence of positive real numbers. Let
be a sequence of positive real numbers. Let  be an array of random variables satisfying (2.15) for some
be an array of random variables satisfying (2.15) for some  . Suppose that the following conditions hold.
. Suppose that the following conditions hold.
(i) .
.
(ii) .
.
(iii) for some
for some  and
and  .
.
Then

and hence,

Proof.
By Remark 2.6, (2.17) implies (2.18). To prove (2.17), we apply Theorem 2.7 with  . Since
. Since  ,
,

Hence the result follows by Theorem 2.7.
The following theorem gives a general method for obtaining the complete moment convergence for maximum partial sums of random variables satisfying condition (2.20).
Theorem 2.9.
Let  be an array of random variables with
be an array of random variables with  for
for  ,
,  . Let
. Let  and
and  be sequences of positive real numbers. Suppose that the following conditions hold.
be sequences of positive real numbers. Suppose that the following conditions hold.
(i)For some  , there exists a positive constant
, there exists a positive constant  depending only on
depending only on  such that
such that

where  .
.
(ii) .
.
(iii) .
.
Then

Proof.
The proof is similar to that of Theorem 2.5. We have by Lemma 2.4, (2.20), (ii), and (iii) that

Hence the result is proved.
Remark 2.10.
If (2.21) holds, then  for all
for all  , since, as in Remark 2.6,
, since, as in Remark 2.6,

When  , we have the following theorem.
, we have the following theorem.
Theorem 2.11.
Let  be an array of random variables with
be an array of random variables with  for
for  ,
,  . Let
. Let  and
and  be sequences of positive real numbers. Suppose that the following conditions hold.
be sequences of positive real numbers. Suppose that the following conditions hold.
(i)For some  , there exists a positive constant
, there exists a positive constant  depending only on
depending only on  such that
such that

where  .
.
(ii) .
.
(iii) .
.
(iv) for some
for some  .
.
Then (2.21) holds.
Proof.
The proof is similar to that of Theorem 2.9 and is omitted.
Corollary 2.12.
Let  be a sequence of positive real numbers. Let
be a sequence of positive real numbers. Let  be an array of random variables satisfying (2.24) for some
be an array of random variables satisfying (2.24) for some  . Suppose that the following conditions hold.
. Suppose that the following conditions hold.
(i) .
.
(ii) .
.
(iii) for some
for some  and
and  .
.
Then

and hence,

Proof.
By Remark 2.10, (2.25) implies (2.26). As in the proof of Corollary 2.8,

Hence the result follows by Theorem 2.11 with  .
.
3. Corollaries
In this section, we establish some complete moment convergence results by using the results obtained in the previous section.
Throughout this section, let  be a sequence of positive even functions satisfying
be a sequence of positive even functions satisfying

for some  .
.
To obtain complete moment convergence results, the following lemmas are needed.
Lemma 3.1.
Let  be a random variable and
be a random variable and  a sequence of positive even functions satisfying (3.1) for some
a sequence of positive even functions satisfying (3.1) for some  . Then for all
. Then for all  and
and  , the followings hold.
, the followings hold.
(i)If  , then
, then  .
.
(ii) .
.
Proof.
First note by  that
that  is an increasing function. If
is an increasing function. If  , then
, then  implies
implies  , and so
, and so

Hence (i) holds. Since  ,
,

So (ii) holds.
Lemma 3.2.
Let  be an array of random variables with
be an array of random variables with  for
for  ,
,  . Let
. Let  and
and  be sequences of positive real numbers. Assume that
be sequences of positive real numbers. Assume that  is a sequence of positive even functions satisfying (3.1) for some
is a sequence of positive even functions satisfying (3.1) for some  and
and

Then the followings hold.
(i)If  , then
, then  .
.
(ii) .
.
Proof.
The result follows from Lemma 3.1.
By using Lemma 3.2, we can obtain Corollaries 3.3, 3.4, 3.5, 3.6 from Theorem 2.5, Corollary 2.8, Theorem 2.9, Corollary 2.12, respectively.
Corollary 3.3.
Let  and
and  be sequences of positive real numbers
be sequences of positive real numbers  a sequence of positive even functions satisfying (3.1) for some
a sequence of positive even functions satisfying (3.1) for some  . Assume that
. Assume that  is an array of random variables satisfying (2.9) for
is an array of random variables satisfying (2.9) for  and (3.4). Then (2.10) holds.
and (3.4). Then (2.10) holds.
Corollary 3.4.
Let  be a sequence of positive real numbers
be a sequence of positive real numbers  a sequence of positive even functions satisfying (3.1) for some
a sequence of positive even functions satisfying (3.1) for some  . Assume that
. Assume that  is an array of random variables satisfying (2.15) for some
is an array of random variables satisfying (2.15) for some  (
( is the same as in (3.6)),
is the same as in (3.6)),


Then (2.17) holds and hence, (2.18) holds.
Corollary 3.5.
Let  and
and  be sequences of positive real numbers
be sequences of positive real numbers  a sequence of positive even functions satisfying (3.1) for some
a sequence of positive even functions satisfying (3.1) for some  . Assume that
. Assume that  is an array of random variables satisfying (2.20) for
is an array of random variables satisfying (2.20) for  and (3.4). Then (2.21) holds.
and (3.4). Then (2.21) holds.
Corollary 3.6.
Let  be a sequence of positive real numbers
be a sequence of positive real numbers  a sequence of positive even functions satisfying (3.1) for some
a sequence of positive even functions satisfying (3.1) for some  . Assume that
. Assume that  is an array of random variables satisfying (2.24) for some
is an array of random variables satisfying (2.24) for some  (
( is the same as in (3.6)), (3.5), and (3.6). Then (2.25) holds and hence, (2.26) holds.
is the same as in (3.6)), (3.5), and (3.6). Then (2.25) holds and hence, (2.26) holds.
Remark 3.7.
Marcinkiewicz-Zygmund and Rosenthal (type) inequalities hold for dependent random variables as well as independent random variables.
-
(1)
For an array
 of rowwise negatively associated random variables, condition (2.20) holds if
of rowwise negatively associated random variables, condition (2.20) holds if  , and (2.24) holds if
, and (2.24) holds if  by Shao's [3] results. Note that
by Shao's [3] results. Note that 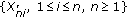 is still an array of rowwise negatively associated random variables. Hence Corollaries 3.3–3.6 hold for arrays of rowwise negatively associated random variables.
is still an array of rowwise negatively associated random variables. Hence Corollaries 3.3–3.6 hold for arrays of rowwise negatively associated random variables. -
(2)
For an array
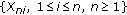 of rowwise negatively orthant dependent random variables, condition (2.9) holds if
of rowwise negatively orthant dependent random variables, condition (2.9) holds if 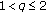 , and (2.15) holds if
, and (2.15) holds if 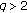 by the results of Asadian et al. [4]. Hence Corollaries 3.3 and 3.4 hold for arrays of rowwise negatively orthant dependent random variables. These results also were proved by Wu and Zhu [13]. Hence Corollaries 3.3 and 3.4 extend the results of Wu and Zhu [13] from an array of negatively orthant dependent random variables to an array of random variables satisfying (2.9) and (2.15).
by the results of Asadian et al. [4]. Hence Corollaries 3.3 and 3.4 hold for arrays of rowwise negatively orthant dependent random variables. These results also were proved by Wu and Zhu [13]. Hence Corollaries 3.3 and 3.4 extend the results of Wu and Zhu [13] from an array of negatively orthant dependent random variables to an array of random variables satisfying (2.9) and (2.15). -
(3)
For an array
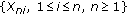 of rowwise
of rowwise 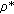 -mixing random variables, condition (2.24) does not necessarily hold if
-mixing random variables, condition (2.24) does not necessarily hold if 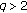 . As mentioned in Section 1, Utev and Peligrad [7] proved (1.4) for
. As mentioned in Section 1, Utev and Peligrad [7] proved (1.4) for 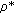 -mixing random variables. However, the constant
-mixing random variables. However, the constant 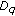 depends on both
depends on both 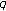 and the sequence of
and the sequence of 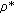 -mixing random variables. Hence condition (2.24) holds for an array of rowwise
-mixing random variables. Hence condition (2.24) holds for an array of rowwise 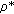 -mixing random variables under the additional condition that
-mixing random variables under the additional condition that 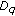 depending on the sequence of random variables in each row are bounded. So Corollary 3.6 holds for arrays of rowwise
depending on the sequence of random variables in each row are bounded. So Corollary 3.6 holds for arrays of rowwise 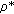 -mixing random variables satisfying this additional condition. Zhu [12] obtained only (2.26) in Corollary 3.6 when the array is rowwise
-mixing random variables satisfying this additional condition. Zhu [12] obtained only (2.26) in Corollary 3.6 when the array is rowwise 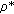 -mixing random variables satisfying the additional condition. This additional condition should be added in Zhu [12]. Hence Corollary 3.6 generalizes and extends Zhu's [12] result from
-mixing random variables satisfying the additional condition. This additional condition should be added in Zhu [12]. Hence Corollary 3.6 generalizes and extends Zhu's [12] result from 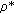 -mixing random variables to more general random variables.
-mixing random variables to more general random variables.
Finally, we apply the complete moment convergence results obtained in the previous section to a sequence of identically distributed random variables.
Corollary 3.8.
Let  be a sequence of identically distributed random variables with
be a sequence of identically distributed random variables with  for some
for some  and
and  . Assume that for any
. Assume that for any  , there exists a positive constant
, there exists a positive constant  depending only on
depending only on  such that
such that

where  . Then (1.7) holds.
. Then (1.7) holds.
Proof.
Let  for
for  ,
,  . We apply Theorem 2.7 with
. We apply Theorem 2.7 with  and
and  . Take
. Take  and
and  such that
such that  ,
,  , and
, and  . Then it is easy to see that
. Then it is easy to see that

Hence the result follows from Theorem 2.7.
Corollary 3.9.
Let  be a sequence of identically distributed random variables with
be a sequence of identically distributed random variables with  for some
for some  and
and  . Assume that for any
. Assume that for any  , there exists a positive constant
, there exists a positive constant  depending only on
depending only on  such that
such that

where  . Then
. Then

Proof.
As in the proof of Corollary 3.8, (3.8) are satisfied. So the result follows from Theorem 2.11.
Remark 3.10.
If  is a sequence of i.i.d. random variables, then conditions (3.7) and (3.9) are satisfied when
is a sequence of i.i.d. random variables, then conditions (3.7) and (3.9) are satisfied when  . Hence Corollaries 3.8 and 3.9 generalize and extend the result of Chow [11]. There are many sequences of dependent random variables satisfying (3.7) for all
. Hence Corollaries 3.8 and 3.9 generalize and extend the result of Chow [11]. There are many sequences of dependent random variables satisfying (3.7) for all  . Examples include sequences of negatively orthant dependent random variables, negatively associated random variables,
. Examples include sequences of negatively orthant dependent random variables, negatively associated random variables,  -mixing random variables,
-mixing random variables,  -mixing identically distributed random variables satisfying
-mixing identically distributed random variables satisfying  , and
, and  -mixing identically distributed random variables satisfying
-mixing identically distributed random variables satisfying  . The above sequences of dependent random variables except negatively orthant dependent random variables also satisfy (3.9) when
. The above sequences of dependent random variables except negatively orthant dependent random variables also satisfy (3.9) when  . Hence Corollaries 3.8 and 3.9 hold for many dependent random variables as well as independent random variables.
. Hence Corollaries 3.8 and 3.9 hold for many dependent random variables as well as independent random variables.
References
Marcinkiewicz J, Zygmund A: Sur les fonctions independantes. Fundamenta Mathematicae 1937, 29: 60–90.
Rosenthal HP: On the subspaces of spanned by sequences of independent random variables. Israel Journal of Mathematics 1970, 8: 273–303. 10.1007/BF02771562
Shao Q-M: A comparison theorem on moment inequalities between negatively associated and independent random variables. Journal of Theoretical Probability 2000,13(2):343–356. 10.1023/A:1007849609234
Asadian N, Fakoor V, Bozorgnia A: Rosenthal's type inequalities for negatively orthant dependent random variables. Journal of the Iranian Statistical Society 2006, 5: 69–75.
Shao Q-M: A moment inequality and its applications. Acta Mathematica Sinica 1988,31(6):736–747.
Shao Q-M: Maximal inequalities for partial sums of -mixing sequences. The Annals of Probability 1995,23(2):948–965. 10.1214/aop/1176988297
Utev S, Peligrad M: Maximal inequalities and an invariance principle for a class of weakly dependent random variables. Journal of Theoretical Probability 2003,16(1):101–115. 10.1023/A:1022278404634
Hsu PL, Robbins H: Complete convergence and the law of large numbers. Proceedings of the National Academy of Sciences of the United States of America 1947, 33: 25–31. 10.1073/pnas.33.2.25
Erdös P: On a theorem of Hsu and Robbins. Annals of Mathematical Statistics 1949, 20: 286–291. 10.1214/aoms/1177730037
Baum LE, Katz M: Convergence rates in the law of large numbers. Transactions of the American Mathematical Society 1965, 120: 108–123. 10.1090/S0002-9947-1965-0198524-1
Chow YS: On the rate of moment convergence of sample sums and extremes. Bulletin of the Institute of Mathematics. Academia Sinica 1988,16(3):177–201.
Zhu M-H: Strong laws of large numbers for arrays of rowwise -mixing random variables. Discrete Dynamics in Nature and Society 2007, 2007:-6.
Wu Y-F, Zhu D-J: Convergence properties of partial sums for arrays of rowwise negatively orthant dependent random variables. Journal of the Korean Statistical Society. In press Journal of the Korean Statistical Society. In press
Acknowledgments
The author would like to thank the referees for the helpful comments and suggestions. This work was supported by the Korea Science and Engineering Foundation (KOSEF) grant funded by the Korea government (MOST) (no. R01-2007-000-20053-0).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sung, S.H. Moment Inequalities and Complete Moment Convergence. J Inequal Appl 2009, 271265 (2009). https://doi.org/10.1155/2009/271265
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/271265
 of rowwise negatively associated random variables, condition (2.20) holds if
of rowwise negatively associated random variables, condition (2.20) holds if  , and (2.24) holds if
, and (2.24) holds if  by Shao's [
by Shao's [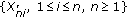 is still an array of rowwise negatively associated random variables. Hence Corollaries 3.3–3.6 hold for arrays of rowwise negatively associated random variables.
is still an array of rowwise negatively associated random variables. Hence Corollaries 3.3–3.6 hold for arrays of rowwise negatively associated random variables.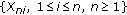 of rowwise negatively orthant dependent random variables, condition (2.9) holds if
of rowwise negatively orthant dependent random variables, condition (2.9) holds if 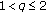 , and (2.15) holds if
, and (2.15) holds if 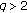 by the results of Asadian et al. [
by the results of Asadian et al. [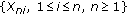 of rowwise
of rowwise 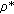 -mixing random variables, condition (2.24) does not necessarily hold if
-mixing random variables, condition (2.24) does not necessarily hold if 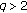 . As mentioned in Section 1, Utev and Peligrad [
. As mentioned in Section 1, Utev and Peligrad [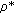 -mixing random variables. However, the constant
-mixing random variables. However, the constant 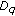 depends on both
depends on both 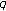 and the sequence of
and the sequence of 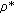 -mixing random variables. Hence condition (2.24) holds for an array of rowwise
-mixing random variables. Hence condition (2.24) holds for an array of rowwise 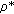 -mixing random variables under the additional condition that
-mixing random variables under the additional condition that 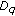 depending on the sequence of random variables in each row are bounded. So Corollary 3.6 holds for arrays of rowwise
depending on the sequence of random variables in each row are bounded. So Corollary 3.6 holds for arrays of rowwise 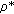 -mixing random variables satisfying this additional condition. Zhu [
-mixing random variables satisfying this additional condition. Zhu [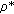 -mixing random variables satisfying the additional condition. This additional condition should be added in Zhu [
-mixing random variables satisfying the additional condition. This additional condition should be added in Zhu [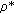 -mixing random variables to more general random variables.
-mixing random variables to more general random variables.