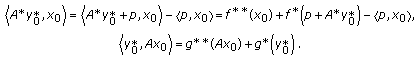- Research Article
- Open access
- Published:
Optimality Conditions and Duality for DC Programming in Locally Convex Spaces
Journal of Inequalities and Applications volume 2009, Article number: 258756 (2009)
Abstract
Consider the DC programming problem  where
where  and
and  are proper convex functions defined on locally convex Hausdorff topological vector spaces
are proper convex functions defined on locally convex Hausdorff topological vector spaces  and
and  respectively, and
respectively, and  is a linear operator from
is a linear operator from  to
to  . By using the properties of the epigraph of the conjugate functions, the optimality conditions and strong duality of
. By using the properties of the epigraph of the conjugate functions, the optimality conditions and strong duality of  are obtained.
are obtained.
1. Introduction
Let  and
and  be real locally convex Hausdorff topological vector spaces, whose respective dual spaces,
be real locally convex Hausdorff topological vector spaces, whose respective dual spaces,  and
and  are endowed with the weak
are endowed with the weak -topologies
-topologies  and
and  . Let
. Let  ,
,  be proper convex functions, and let
be proper convex functions, and let  be a linear operator such that
be a linear operator such that  . We consider the primal DC (difference of convex) programming problem
. We consider the primal DC (difference of convex) programming problem

and its associated dual problem

where  and
and  are the Fenchel conjugates of
are the Fenchel conjugates of  and
and  , respectively, and
, respectively, and  stands for the adjoint operator, where
stands for the adjoint operator, where  is the subspace of
is the subspace of  such that
such that  if and only if
if and only if  defined by
defined by  is continuous on
is continuous on  . Note that, in general,
. Note that, in general,  is not the whole space
is not the whole space  because
because  is not necessarily continuous.
is not necessarily continuous.
Problems of DC programming are highly important from both viewpoints of optimization theory and applications. They have been extensively studied in the literature; see, for example, [1–6] and the references therein. On one hand, such problems being heavily nonconvex can be considered as a special class in nondifferentiable programming (in particular, quasidifferentiable programming [7]) and thus are suitable for applying advanced techniques of variational analysis and generalized differentiation developed, for example, in [7–10]. On the other hand, the special convex structure of both plus function  and minus function
and minus function  in the objective of (1.1) offers the possibility to use powerful tools of convex analysis in the study of DC Programming.
in the objective of (1.1) offers the possibility to use powerful tools of convex analysis in the study of DC Programming.
DC programming of type (1.1) (when  is an identity operator) has been considered in the
is an identity operator) has been considered in the  space in paper [5], where the authors obtained some necessary optimality conditions for local minimizers to (1.1) by using refined techniques and results of convex analysis. In this paper, we extend these results to DC programming in topological vector spaces and also derive some new necessary and/or sufficient conditions for local minimizers to (1.1). Finally, we consider the strong duality of problem (1.1); that is, there is no duality gap between the problem
space in paper [5], where the authors obtained some necessary optimality conditions for local minimizers to (1.1) by using refined techniques and results of convex analysis. In this paper, we extend these results to DC programming in topological vector spaces and also derive some new necessary and/or sufficient conditions for local minimizers to (1.1). Finally, we consider the strong duality of problem (1.1); that is, there is no duality gap between the problem  and the dual problem
and the dual problem  and
and  has at least an optimal solution.
has at least an optimal solution.
In this paper we study the optimality conditions and the strong duality between  and
and  in the most general setting, namely, when
in the most general setting, namely, when  and
and  are proper convex functions (not necessarily lower semicontinuous) and
are proper convex functions (not necessarily lower semicontinuous) and  is a linear operator (not necessarily continuous). The rest of the paper is organized as follows. In Section 2 we present some basic definitions and preliminary results. The optimality conditions are derived in Section 3, and the strong duality of DC programming is obtained in Section 4.
is a linear operator (not necessarily continuous). The rest of the paper is organized as follows. In Section 2 we present some basic definitions and preliminary results. The optimality conditions are derived in Section 3, and the strong duality of DC programming is obtained in Section 4.
2. Notations and Preliminary Results
The notation used in the present paper is standard (cf. [11]). In particular, we assume throughout the paper that  and
and  are real locally convex Hausdorff topological vector spaces, and let
are real locally convex Hausdorff topological vector spaces, and let  denote the dual space, endowed with the weak
denote the dual space, endowed with the weak -topology
-topology  By
By  we will denote the value of the functional
we will denote the value of the functional  at
at  , that is,
, that is,  . The zero of each of the involved spaces will be indistinctly represented by
. The zero of each of the involved spaces will be indistinctly represented by 
Let  be a proper convex function. The effective domain and the epigraph of
be a proper convex function. The effective domain and the epigraph of  are the nonempty sets defined by
are the nonempty sets defined by

The conjugate function of  is the function
is the function  defined by
defined by

If  is lower semicontinuous, then the following equality holds:
is lower semicontinuous, then the following equality holds:

Let  . For each
. For each  , the
, the  -subdifferential of
-subdifferential of  at
at  is the convex set defined by
is the convex set defined by

When  , we put
, we put  . If
. If  in (2.4), the set
in (2.4), the set  is the classical subdifferential of convex analysis, that is,
is the classical subdifferential of convex analysis, that is,

Let  , the following inequality holds (cf. [11, Theorem
, the following inequality holds (cf. [11, Theorem  (ii)] ):
(ii)] ):

Following [12],

The Young equality holds

As a consequence of that,

The following notion of Cartesian product map is used in [13].
Definition 2.1.
Let  be nonempty sets and consider maps
be nonempty sets and consider maps  and
and  . We denote by
. We denote by  the map defined by
the map defined by

3. Optimality Conditions
Let  denote the identity map on
denote the identity map on  . We consider the image set
. We consider the image set  of
of  through the map
through the map  , that is,
, that is,

By [14, Proposition 4.1] and the well-known characterization of optimal solution to DC problem, we obtain the following lemma.
Lemma 3.1.
Let  be proper convex fucntions on
be proper convex fucntions on  , and let
, and let  . Then
. Then  is a local minimizer of
is a local minimizer of  if and only if, for each
if and only if, for each 

Especially, if  is a local minimizer of
is a local minimizer of  , then
, then

Theorem 3.2.
The following statements are equivalent:
(i)
(ii)For each  and each
and each  ,
,

Moreover,  is a local optimal solution to problem
is a local optimal solution to problem  if and only if for each
if and only if for each  ,
,

Proof.
(i) (ii). Suppose that (i) holds. Let
(ii). Suppose that (i) holds. Let  , and
, and  , then for each
, then for each  ,
,

Therefore,  . Hence,
. Hence,  .
.
Conversely, let  . Then
. Then  . By (i),
. By (i),

Therefore, there exists  such that
such that  and
and  . Noting that
. Noting that  , then
, then

This implies  thanks to (2.6). Thus,
thanks to (2.6). Thus,  and
and  . Hence, (3.4) is seen to hold.
. Hence, (3.4) is seen to hold.
(ii) (i). Suppose that (ii) holds. To show (i), it suffices to show that
(i). Suppose that (ii) holds. To show (i), it suffices to show that  . To do this, let
. To do this, let  and
and  . By (2.7), there exists
. By (2.7), there exists  such that
such that  and
and  From (3.4), there exists
From (3.4), there exists  such that
such that  . Since
. Since  , it follows from (2.6) that
, it follows from (2.6) that

that is  . Hence,
. Hence,  and so
and so  .
.
By the well-known characterization of optimal solution to DC problem (see Lemma 3.1),  is a local optimal solution to problem
is a local optimal solution to problem  if and only if, for each
if and only if, for each  ,
,

Obviously,  holds automatically. The proof is complete.
holds automatically. The proof is complete.
Let  . Define
. Define

Theorem 3.3.
The following statements are equivalent:
(i) ,
,
(ii)For each  and each
and each  ,
,

Moreover,  is a local optimal solution to problem
is a local optimal solution to problem  if and only if, for each
if and only if, for each  ,
,

Proof.
(i) (ii). Suppose that (i) holds. Let
(ii). Suppose that (i) holds. Let  and
and  . Then one has
. Then one has

Hence,  By the given assumption,
By the given assumption,

Therefore, there exists  such that
such that  and
and  . Hence,
. Hence,  , this means
, this means  and so
and so  . Consequently,
. Consequently,  . This completes the proof because the converse inclusion holds automatically.
. This completes the proof because the converse inclusion holds automatically.
(ii) (i). Suppose that (ii) holds. To show (i), it suffice to show that
(i). Suppose that (ii) holds. To show (i), it suffice to show that  . To do this, let
. To do this, let  and
and  . By (2.7), there exists
. By (2.7), there exists  such that
such that  and
and  . From (3.12), there exists
. From (3.12), there exists  such that
such that  . Since
. Since  , it follows from (2.6) that
, it follows from (2.6) that

that is  . Hence,
. Hence,  and so
and so  .
.
Similar to the proof of (3.5), one has that (3.13) holds.
4. Duality in DC Programming
This section is devoted to study the strong duality between the primal problem and its Toland dual, namely, the property that both optimal values coincide and the dual problem has at least an optimal solution.
Given  , we consider the DC programming problem given in the form
, we consider the DC programming problem given in the form

and the corresponding dual problem

Let  denote the optimal values of problems
denote the optimal values of problems  and
and  , respectively, that is
, respectively, that is

In the special case when  , problems
, problems  and
and  are just the problem
are just the problem  and
and  .
.
Before establishing the relationship between problems  and
and  , we give useful formula for computing the values of conjugate functions. The formula is an extension of a well-known result, called Toland duality, for DC problems. In this section, we always assume that
, we give useful formula for computing the values of conjugate functions. The formula is an extension of a well-known result, called Toland duality, for DC problems. In this section, we always assume that  and
and  are everywhere subdifferentible.
are everywhere subdifferentible.
Proposition 4.1.
Let  . Then the conjugate function
. Then the conjugate function  of
of  is given by
is given by

Proof.
By the definition of conjugate function, it follows that

Next, we prove that

Suppose on the contrary that  that is, there exists
that is, there exists  such that
such that

Let  and
and  , then
, then

From this, it follows that

which is contradiction to (4.7), and so (4.4) holds.
Following from Proposition 4.1, we obtain the following proposition.
Proposition 4.2.
For each  ,
,

Proof.
Let  . Since
. Since  , it follows from (4.4) that
, it follows from (4.4) that

Remark 4.3.
In the special case when  and
and  , formula (4.10) was first given by Pshenichnyi (see [10]) and related results on duality can be found in [15–17].
, formula (4.10) was first given by Pshenichnyi (see [10]) and related results on duality can be found in [15–17].
Proposition 4.4.
For each  ,
,
(i)if  is an optimal solution to problem
is an optimal solution to problem  , then
, then  is an optimal solution to problem
is an optimal solution to problem  ;
;
(ii)suppose that  and
and  are lower semicontinuous. If
are lower semicontinuous. If  is an optimal solution to problem
is an optimal solution to problem  , then
, then  is an optimal solution to problem
is an optimal solution to problem  .
.
Proof.
-
(i)
Let
 be an optimal solution to problem
be an optimal solution to problem  and let
and let  . Then
. Then  . It follows from (3.5) that
. It follows from (3.5) that 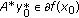 . By the Young equality, we have
. By the Young equality, we have 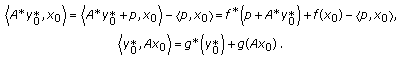 (4.12)
(4.12)
Therefore,

By (4.10),  is an optimal solution to problem
is an optimal solution to problem  .
.
-
(ii)
Let
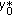 be an optimal solution to problem
be an optimal solution to problem 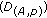 and
and 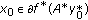 . Then
. Then 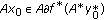 and hence
and hence 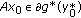 thanks to Theorem 3.3. By the Young equality, we have
thanks to Theorem 3.3. By the Young equality, we have 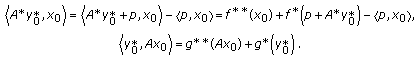 (4.14)
(4.14)
Since the functions  and
and  are lower semicontinuous, it follows from (2.3) that
are lower semicontinuous, it follows from (2.3) that  and
and  . Hence, by the above two equalities, one has
. Hence, by the above two equalities, one has

By (4.10),  is an optimal solution to problem
is an optimal solution to problem  .
.
Obviously, if  is continuous, then
is continuous, then  and so
and so  for each
for each  . By Propositions 4.2 and 4.4, we get the following strong duality theorem straightforwardly.
. By Propositions 4.2 and 4.4, we get the following strong duality theorem straightforwardly.
Theorem 4.5.
For each  ,
,
(i)suppose that  is continuous. If the problem
is continuous. If the problem  has an optimal solution, then
has an optimal solution, then  and
and  has an optimal solution;
has an optimal solution;
(ii)suppose that  and
and  are lower semicontinuous. If the problem
are lower semicontinuous. If the problem  has an optimal solution, then
has an optimal solution, then  and
and  has an optimal solution.
has an optimal solution.
Corollary 4.6.
( ) If the problem
) If the problem  has an optimal solution, then
has an optimal solution, then  and
and  has an optimal solution.
has an optimal solution.
( )Suppose that
)Suppose that  and
and  are lower semicontinuous. If the problem
are lower semicontinuous. If the problem  has an optimal solution, then
has an optimal solution, then  and
and  has an optimal solution.
has an optimal solution.
Remark 4.7.
As in [13], if  and
and  has an optimal solution, then we say the converse duality holds between
has an optimal solution, then we say the converse duality holds between  and
and  .
.
Example 4.8.
Let  and let
and let  Define
Define  by
by

Then the conjugate functions  and
and  are
are

Obviously,  and
and  attained the infimun at
attained the infimun at  ,
,  and
and  attained the infimum at
attained the infimum at  . Hence,
. Hence,  . It is easy to see that
. It is easy to see that  and
and  . Therefore, Proposition 4.4 is seen to hold and Theorem 4.5 is applicable.
. Therefore, Proposition 4.4 is seen to hold and Theorem 4.5 is applicable.
References
An LTH, Tao PD: The DC (difference of convex functions) programming and DCA revisited with DC models of real world nonconvex optimization problems. Annals of Operations Research 2005, 133: 23–46. 10.1007/s10479-004-5022-1
Bot RI, Wanka G: Duality for multiobjective optimization problems with convex objective functions and D.C. constraints. Journal of Mathematical Analysis and Applications 2006,315(2):526–543. 10.1016/j.jmaa.2005.06.067
Dinh N, Nghia TTA, Vallet G: A closedness condition and its applications to DC programs with convex constraints. Optimization 2008, 1: 235–262.
Dinh N, Vallet G, Nghia TTA: Farkas-type results and duality for DC programs with convex constraints. Journal of Convex Analysis 2008,15(2):235–262.
Horst R, Thoai NV: DC programming: overview. Journal of Optimization Theory and Applications 1999,103(1):1–43. 10.1023/A:1021765131316
Martínez-Legaz J-E, Volle M: Duality in D.C. programming: the case of several D.C. constraints. Journal of Mathematical Analysis and Applications 1999,237(2):657–671. 10.1006/jmaa.1999.6496
Demyanov VF, Rubinov AM: Constructive Nonsmooth Analysis, Approximation & Optimization. Volume 7. Peter Lang, Frankfurt, Germany; 1995:iv+416.
Mordukhovich BS: Variational Analysis and Generalized Differentiation. I: Basic Theory, Grundlehren der Mathematischen Wissenschaften. Volume 330. Springer, Berlin, Germany; 2006:xxii+579.
Mordukhovich BS: Variational Analysis and Generalized Differentiation. II: Application, Grundlehren der Mathematischen Wissenschaften. Volume 331. Springer, Berlin, Germany; 2006:i–xxii and 1–610.
Rockafellar RT, Wets RJ-B: Variational Analysis, Grundlehren der Mathematischen Wissenschaften. Volume 317. Springer, Berlin, Germany; 1998:xiv+733.
Zalinescu C: Convex Analysis in General Vector Spaces. World Scientific, River Edge, NJ, USA; 2002:xx+367.
Jeyakumar V, Lee GM, Dinh N: New sequential Lagrange multiplier conditions characterizing optimality without constraint qualification for convex programs. SIAM Journal on Optimization 2003,14(2):534–547. 10.1137/S1052623402417699
Bot RI, Wanka G: A weaker regularity condition for subdifferential calculus and Fenchel duality in infinite dimensional spaces. Nonlinear Analysis: Theory, Methods & Applications 2006,64(12):2787–2804. 10.1016/j.na.2005.09.017
Mordukhovich BS, Nam NM, Yen ND: Fréchet subdifferential calculus and optimality conditions in nondifferentiable programming. Optimization 2006,55(5–6):685–708. 10.1080/02331930600816395
Singer I: A general theory of dual optimization problems. Journal of Mathematical Analysis and Applications 1986,116(1):77–130. 10.1016/0022-247X(86)90046-6
Singer I: Some further duality theorems for optimization problems with reverse convex constraint sets. Journal of Mathematical Analysis and Applications 1992,171(1):205–219. 10.1016/0022-247X(92)90385-Q
Volle M: Concave duality: application to problems dealing with difference of functions. Mathematical Programming 1988,41(2):261–278.
Acknowledgment
The author wish to thank the referees for careful reading of this paper and many valuable comments, which helped to improve the quality of the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, X. Optimality Conditions and Duality for DC Programming in Locally Convex Spaces. J Inequal Appl 2009, 258756 (2009). https://doi.org/10.1155/2009/258756
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/258756
 be an optimal solution to problem
be an optimal solution to problem 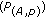 and let
and let  . Then
. Then  . It follows from (3.5) that
. It follows from (3.5) that 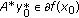 . By the Young equality, we have
. By the Young equality, we have 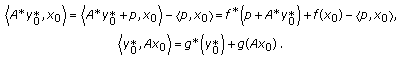
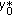 be an optimal solution to problem
be an optimal solution to problem 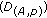 and
and 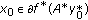 . Then
. Then 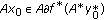 and hence
and hence 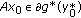 thanks to Theorem 3.3. By the Young equality, we have
thanks to Theorem 3.3. By the Young equality, we have