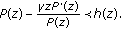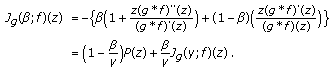- Research Article
- Open access
- Published:
Subclasses of Meromorphic Functions Associated with Convolution
Journal of Inequalities and Applications volume 2009, Article number: 190291 (2009)
Abstract
Several subclasses of meromorphic functions in the unit disk are introduced by means of convolution with a given fixed meromorphic function. Subjecting each convoluted-derived function in the class to be subordinated to a given normalized convex function with positive real part, these subclasses extend the classical subclasses of meromorphic starlikeness, convexity, close-to-convexity, and quasi-convexity. Class relations, as well as inclusion and convolution properties of these subclasses, are investigated.
1. Introduction
Let  be the set of all analytic functions defined in the unit disk
be the set of all analytic functions defined in the unit disk  . We denote by
. We denote by  the class of normalized analytic functions
the class of normalized analytic functions  defined in
defined in  . For two functions
. For two functions  and
and  analytic in
analytic in  , the function
, the function  is subordinate to
is subordinate to  , written as
, written as

if there exists a Schwarz function  , analytic in
, analytic in  with
with  and
and  such that
such that  In particular, if the function
In particular, if the function  is univalent in
is univalent in  , then
, then  is equivalent to
is equivalent to  and
and 
A function  is starlike if
is starlike if  is subordinate to
is subordinate to  and convex if
and convex if  is subordinate to
is subordinate to  . Ma and Minda [1] gave a unified presentation of these classes and introduced the classes
. Ma and Minda [1] gave a unified presentation of these classes and introduced the classes

where  is an analytic function with positive real part,
is an analytic function with positive real part,  , and
, and  maps the unit disk
maps the unit disk  onto a region starlike with respect to 1.
onto a region starlike with respect to 1.
The convolution or the Hadamard product of two analytic functions  and
and  is given by
is given by

In term of convolution, a function  is starlike if
is starlike if  is starlike, and convex if
is starlike, and convex if  is starlike. These ideas led to the study of the class of all functions
is starlike. These ideas led to the study of the class of all functions  such that
such that  is starlike for some fixed function
is starlike for some fixed function  in
in  In this direction, Shanmugam [2] introduced and investigated various subclasses of analytic functions by using the convex hull method [3–5] and the method of differential subordination. Ravichandran [6] introduced certain classes of analytic functions with respect to
In this direction, Shanmugam [2] introduced and investigated various subclasses of analytic functions by using the convex hull method [3–5] and the method of differential subordination. Ravichandran [6] introduced certain classes of analytic functions with respect to  -ply symmetric points, conjugate points, and symmetric conjugate points, and also discussed their convolution properties. Some other related studies were also made in [7–9], and more recently by Shamani et al. [10].
-ply symmetric points, conjugate points, and symmetric conjugate points, and also discussed their convolution properties. Some other related studies were also made in [7–9], and more recently by Shamani et al. [10].
Let  denote the class of meromorphic functions
denote the class of meromorphic functions  of the form
of the form

which are analytic and univalent in the punctured unit disk  . For
. For  we recall that the classes of meromorphic starlike, meromorphic convex, meromorphic close-to-convex, meromorphic
we recall that the classes of meromorphic starlike, meromorphic convex, meromorphic close-to-convex, meromorphic  -convex (Mocanu sense), and meromorphic quasi-convex functions of order
-convex (Mocanu sense), and meromorphic quasi-convex functions of order  , denoted by
, denoted by  ,
,  ,
,  ,
,  and
and  respectively, are defined by
respectively, are defined by

The convolution of two meromorphic functions  and
and  , where
, where  is given by (1.4) and
is given by (1.4) and  , is given by
, is given by

Motivated by the investigation of Shanmugam [2], Ravichandran [6], and Ali et al. [7, 11], several subclasses of meromorphic functions defined by means of convolution with a given fixed meromorphic function are introduced in Section 2. These new subclasses extend the classical classes of meromorphic starlike, convex, close-to-convex,  -convex, and quasi-convex functions given in (1.5). Section 3 is devoted to the investigation of the class relations as well as inclusion and convolution properties of these newly defined classes.
-convex, and quasi-convex functions given in (1.5). Section 3 is devoted to the investigation of the class relations as well as inclusion and convolution properties of these newly defined classes.
We will need the following definition and results to prove our main results.
Let  denote the class of starlike functions of order
denote the class of starlike functions of order  . The class
. The class  of prestarlike functions of order
of prestarlike functions of order  is defined by
is defined by

for  , and
, and

Theorem 1.1 (see [12, Theorem 2.4]).
Let  ,
,  , and
, and  . Then, for any analytic function
. Then, for any analytic function  ,
,

,
where  denotes the closed convex hull of
denotes the closed convex hull of  .
.
Theorem 1.2 (see [13]).
Let  be convex in
be convex in  and
and  with
with  . If
. If  is analytic in
is analytic in  with
with  , then
, then

2. Definitions
In this section, various subclasses of  are defined by means of convolution and subordination. Let
are defined by means of convolution and subordination. Let  be a fixed function in
be a fixed function in  , and let
, and let  be a convex univalent function with positive real part in
be a convex univalent function with positive real part in  and
and  .
.
Definition 2.1.
The class  consists of functions
consists of functions  satisfying
satisfying  in
in  and the subordination
and the subordination

Remark 2.2.
If  , then
, then  coincides with
coincides with  , where
, where

Definition 2.3.
The class  consists of functions
consists of functions  satisfying
satisfying  in
in  and the subordination
and the subordination

Definition 2.4.
The class  consists of functions
consists of functions  such that
such that  in
in  for some
for some  and satisfying the subordination
and satisfying the subordination

Definition 2.5.
For  real, the class
real, the class  consists of functions
consists of functions  satisfying
satisfying  ,
,  in
in  and the subordination
and the subordination

Definition 2.6.
The class  consists of functions
consists of functions  such that
such that  in
in  for some
for some  and satisfying the subordination
and satisfying the subordination

3. Main Results
This section is devoted to the investigation of class relations as well as inclusion and convolution properties of the new subclasses given in Section 2.
Theorem 3.1.
Let  be a convex univalent function satisfying
be a convex univalent function satisfying  , and
, and  with
with  . If
. If  , then
, then  . Equivalently, if
. Equivalently, if  , then
, then  .
.
Proof.
Define the function  by
by

For  , it follows that
, it follows that

and therefore,

Hence  . A computation shows that
. A computation shows that

Theorem 1.1 yields

and because  , it follows that
, it follows that

Theorem 3.2.
The function  if and only if
if and only if 
Proof.
The results follow from the equivalence relations

Theorem 3.3.
Let  be a convex univalent function satisfying
be a convex univalent function satisfying  and
and  with
with  . If
. If  , then
, then  .
.
Proof.
Since  , it follows that
, it follows that

and thus

Let

A similar computation as in the proof of Theorem 3.1 yields

Inequality (3.9) shows that  . Therefore Theorem 1.1 yields
. Therefore Theorem 1.1 yields

hence  .
.
Corollary 3.4.
 under the conditions of Theorem 3.3 .
under the conditions of Theorem 3.3 .
Proof.
The proof follows from (3.12).
In particular, when  , the following corollary is obtained.
, the following corollary is obtained.
Corollary 3.5.
Let  and
and  satisfy the conditions of Theorem 3.3 . If
satisfy the conditions of Theorem 3.3 . If  , then
, then  .
.
Theorem 3.6.
Let  and
and  satisfy the conditions of Theorem 3.3. If
satisfy the conditions of Theorem 3.3. If  , then
, then  . Equivalently
. Equivalently  .
.
Proof.
If  , it follows from Theorem 3.2 that
, it follows from Theorem 3.2 that  . Theorem 3.3 shows that
. Theorem 3.3 shows that  Hence
Hence  .
.
Theorem 3.7.
Under the conditions of Theorem 3.3, if  with respect to
with respect to  , then
, then  with respect to
with respect to  .
.
Proof.
Theorem 3.3 shows that  . Since
. Since  , (3.9) yields
, (3.9) yields  .
.
Let the function  be defined by
be defined by

A similar computation as in the proof of Theorem 3.1 yields

Since  and
and  , it follows from Theorem 1.1 that
, it follows from Theorem 1.1 that

Thus  with respect to
with respect to  .
.
Corollary 3.8.
 under the assumptions of Theorem 3.3 .
under the assumptions of Theorem 3.3 .
Proof.
The subordination (3.15) shows that  .
.
Theorem 3.9.
Let  . Then
. Then
(i) ,
,
(ii) for
for  .
.
Proof.
Define the function  by
by

and the function  by
by

For  , it follows that
, it follows that  Note also that
Note also that

-
(i)
Since
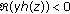 and
and 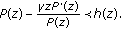 (3.19)
(3.19)
Theorem 1.2 yields  Hence
Hence  .
.
-
(ii)
Observe that
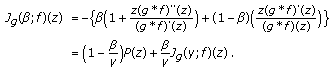 (3.20)
(3.20)
Furthermore  and
and  from (i). Since
from (i). Since  and
and  is convex, we deduce that
is convex, we deduce that  . Therefore,
. Therefore, 
Corollary 3.10.
The class
 is a subset of the class
is a subset of the class

Proof.
The proof follows from the definition of the classes by taking  .
.
Theorem 3.11.
The function  if and only if
if and only if  .
.
Proof.
If  , then there exists
, then there exists  such that
such that

Also,

Since  , by Theorem 3.2 ,
, by Theorem 3.2 ,  . Hence
. Hence  .
.
Conversely, if  , then
, then

for some  . Let
. Let  be such that
be such that  . The proof is completed by observing that
. The proof is completed by observing that

Corollary 3.12.
Let  and
and  satisfy the conditions of Theorem 3.3 . If
satisfy the conditions of Theorem 3.3 . If  , then
, then 
Proof.
If  , Theorem 3.11 gives
, Theorem 3.11 gives  Theorem 3.7 next gives
Theorem 3.7 next gives  Thus, Theorem 3.11 yields
Thus, Theorem 3.11 yields 
Corollary 3.13.

under the conditions of Theorem 3.3.
Proof.
If  , it follows from Corollary 3.12 that
, it follows from Corollary 3.12 that  The subordination
The subordination

gives  . Therefore
. Therefore 
Open Problem
An analytic convex function in the unit disk is necessarily starlike. For the meromorphic case, is it true that  ?
?
References
Ma WC, Minda D: A unified treatment of some special classes of univalent functions. In Proceedings of the Conference on Complex Analysis (Tianjin, 1992), 1994, Cambridge, Mass, USA, Conference Proceedings and Lecture Notes in Analysis, I. International Press; 157–169.
Shanmugam TN: Convolution and differential subordination. International Journal of Mathematics and Mathematical Sciences 1989,12(2):333–340. 10.1155/S0161171289000384
Barnard RW, Kellogg C: Applications of convolution operators to problems in univalent function theory. The Michigan Mathematical Journal 1980,27(1):81–94.
Parvatham R, Radha S: On -starlike and -close-to-convex functions with respect to -symmetric points. Indian Journal of Pure and Applied Mathematics 1986,17(9):1114–1122.
Ruscheweyh S, Sheil-Small T: Hadamard products of Schlicht functions and the Pólya-Schoenberg conjecture. Commentarii Mathematici Helvetici 1973, 48: 119–135. 10.1007/BF02566116
Ravichandran V: Functions starlike with respect to -ply symmetric, conjugate and symmetric conjugate points. The Journal of the Indian Academy of Mathematics 2004,26(1):35–45.
Ali RM, Ravichandran V, Lee SK: Subclasses of multivalent starlike and convex functions. to appear in Bulletin of the Belgian Mathematical Society. Simon Stevin to appear in Bulletin of the Belgian Mathematical Society. Simon Stevin
Padmanabhan KS, Parvatham R: Some applications of differential subordination. Bulletin of the Australian Mathematical Society 1985,32(3):321–330. 10.1017/S0004972700002410
Padmanabhan KS, Parvatham R: Some applications of differential subordination. Bulletin of the Australian Mathematical Society 1985,32(3):321–330. 10.1017/S0004972700002410
Shamani S, Ali RM, Ravichandran V, Lee SK: Convolution and differential subordination for multivalent functions. to appear in Bulletin of the Malaysian Mathematical Sciences Society. Second Series to appear in Bulletin of the Malaysian Mathematical Sciences Society. Second Series
Ali RM, Ravichandran V, Seenivasagan N: Subordination and superordination of the Liu-Srivastava linear operator on meromorphic functions. Bulletin of the Malaysian Mathematical Sciences Society. Second Series 2008,31(2):193–207.
Ruscheweyh S: Convolutions in Geometric Function Theory: Fundamental Theories of Physics, Séminaire de Mathématiques Supérieures. Volume 83. Presses de l'Université de Montréal, Montreal, Canada; 1982:168.
Eenigenburg P, Miller SS, Mocanu PT, Reade MO: On a Briot-Bouquet differential subordination. Revue Roumaine de Mathématiques Pures et Appliquées 1984,29(7):567–573.
Acknowledgment
The work presented here was supported in part by the USM's Reserach University grant and the FRGS grant
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Haji Mohd, M., Ali, R.M., Keong, L.S. et al. Subclasses of Meromorphic Functions Associated with Convolution. J Inequal Appl 2009, 190291 (2009). https://doi.org/10.1155/2009/190291
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/190291
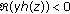 and
and