- Research Article
- Open access
- Published:
Some Strong Limit Theorems for Weighted Product Sums of  -Mixing Sequences of Random Variables
-Mixing Sequences of Random Variables
Journal of Inequalities and Applications volume 2009, Article number: 174768 (2009)
Abstract
We study almost sure convergence for  -mixing sequences of random variables. Many of the previous results are our special cases. For example, the authors extend and improve the corresponding results of Chen et al. (1996) and Wu and Jiang (2008). We extend the classical Jamison convergence theorem and the Marcinkiewicz strong law of large numbers for independent sequences of random variables to
-mixing sequences of random variables. Many of the previous results are our special cases. For example, the authors extend and improve the corresponding results of Chen et al. (1996) and Wu and Jiang (2008). We extend the classical Jamison convergence theorem and the Marcinkiewicz strong law of large numbers for independent sequences of random variables to  -mixing sequences of random variables without necessarily adding any extra conditions.
-mixing sequences of random variables without necessarily adding any extra conditions.
1. Introduction and Lemmas
Let  be a probability space. The random variables we deal with are all defined on
be a probability space. The random variables we deal with are all defined on  . Let
. Let  be a sequence of random variables. For each nonempty set
be a sequence of random variables. For each nonempty set  , and write
, and write  . Given
. Given  -algebras
-algebras  in
in  , let
, let

where  . Define the
. Define the  -mixing coefficients by
-mixing coefficients by

Obviously  and
and  except in the trivial case where all of the random variables
except in the trivial case where all of the random variables  are degenerate.
are degenerate.
Definition 1.1.
A random variables sequence  is said to be a
is said to be a  -mixing random variables sequence if there exists
-mixing random variables sequence if there exists  such that
such that  .
.

-mixing is similar to  -mixing, but both are quite different. A number of writers have studied
-mixing, but both are quite different. A number of writers have studied  -mixing random variables sequences and a series of useful results have been established. We refer to Bradley [1] (which assumes
-mixing random variables sequences and a series of useful results have been established. We refer to Bradley [1] (which assumes  in the central limit theorem), Bryc and Smoleński [2], Goldie and Greenwood [3] (which assumes
in the central limit theorem), Bryc and Smoleński [2], Goldie and Greenwood [3] (which assumes  ), and Yang [4] for moment inequalities and the strong law of large numbers, Wu [5, 6], Wu and Jiang [7], Peligrad and Gut [8], and Gan [9] for almost sure convergence and Utev and Peligrad [10] for maximal inequalities and the invariance principle. When these are compared with the corresponding results of independent random variables sequences, there still remains much to be desired.
), and Yang [4] for moment inequalities and the strong law of large numbers, Wu [5, 6], Wu and Jiang [7], Peligrad and Gut [8], and Gan [9] for almost sure convergence and Utev and Peligrad [10] for maximal inequalities and the invariance principle. When these are compared with the corresponding results of independent random variables sequences, there still remains much to be desired.
Lemma 1.2 (see [7, Theorem  ]).
]).
Let  be a
be a  -mixing sequence of random variables which satisfies
-mixing sequence of random variables which satisfies

Then  converges almost surely (a.s.) and in quadratic mean.
converges almost surely (a.s.) and in quadratic mean.
Lemma 1.3 (see [11, Lemma  ]).
]).
For each positive integer  , let
, let  denote the set of all vectors
denote the set of all vectors  such that
such that  .
.
Then for each positive integer  , there exists a function
, there exists a function  such that the following holds.
such that the following holds.
For any integer  and any choice of real numbers
and any choice of real numbers  , one has that
, one has that

2. Main Results and the Proof
To state our results, we need some notions. Throughout this paper, let  be a sequence of positive real numbers, and let
be a sequence of positive real numbers, and let  satisfy
satisfy  .
.
Jamison et al. [12] proved the following result. Suppose that  are i.i.d. random variables with
are i.i.d. random variables with  . Denote
. Denote  , that is, the number of subscripts
, that is, the number of subscripts  such that
such that  . If
. If  , then
, then  a.s. Chen et al. [13] extended the Jamison Theorem and obtained the following result. Suppose that
a.s. Chen et al. [13] extended the Jamison Theorem and obtained the following result. Suppose that  are i.i.d. random variables with
are i.i.d. random variables with  for some
for some  . If
. If  , then
, then  a.s.
a.s.
The main purpose of this paper is to study the strong limit theorems for weighted sums of  -mixing random variables sequences and try to obtain some new results. We establish weighted partial sums and weighted product sums strong convergence theorems. Our results in this paper extend and improve the corresponding results of Chen et al. [13], Wu and Jiang [7], the classical Jamison convergence theorem, and the Marcinkiewicz strong law of large numbers for independent sequences of random variables to
-mixing random variables sequences and try to obtain some new results. We establish weighted partial sums and weighted product sums strong convergence theorems. Our results in this paper extend and improve the corresponding results of Chen et al. [13], Wu and Jiang [7], the classical Jamison convergence theorem, and the Marcinkiewicz strong law of large numbers for independent sequences of random variables to  -mixing sequences of random variables.
-mixing sequences of random variables.
Theorem 2.1.
Let  be a sequence of
be a sequence of  -mixing random variables with
-mixing random variables with  , and let the following conditions be satisfied:
, and let the following conditions be satisfied:



where  Then
Then

Theorem 2.2.
Suppose that the assumptions of Theorem 2.1 hold, and also suppose

Then for all 

Corollary 2.3.
Let  be a sequence of
be a sequence of  -mixing identically distributed random variables. Let for some
-mixing identically distributed random variables. Let for some 


Then (2.6) holds.
Remark 2.4.
Let  be i.i.d. random variables, and
be i.i.d. random variables, and  in Corollary 2.3, then Corollary 2.3 is the well-known Jamison convergence theorem. Thus, our Theorem 2.2 and Corollary 2.3 generalize and improve the Jamison convergence theorem from the i.i.d. case to
in Corollary 2.3, then Corollary 2.3 is the well-known Jamison convergence theorem. Thus, our Theorem 2.2 and Corollary 2.3 generalize and improve the Jamison convergence theorem from the i.i.d. case to  -mixing sequence. In addition, by Theorems
-mixing sequence. In addition, by Theorems  and
and  in Chen et al. [13] are special situation of Corollary 2.3.
in Chen et al. [13] are special situation of Corollary 2.3.
Theorem 2.5.
Let  be a sequence of
be a sequence of  -mixing random variables. Let
-mixing random variables. Let  be a sequence of positive real numbers with
be a sequence of positive real numbers with  and let the following conditions be satisfied:
and let the following conditions be satisfied:



Then for all 

Corollary 2.6.
Let  be a
be a  -mixing identically distributed random variable sequence, for
-mixing identically distributed random variable sequence, for  , and for
, and for  . Then for all
. Then for all 

In particular, taking  , the above formula is the well-known Marcinkiewicz strong law of large numbers. Thus, our Theorem 2.5 and Corollary 2.6 generalize and improve the Marcinkiewicz strong law of large numbers from the i.i.d. case to
, the above formula is the well-known Marcinkiewicz strong law of large numbers. Thus, our Theorem 2.5 and Corollary 2.6 generalize and improve the Marcinkiewicz strong law of large numbers from the i.i.d. case to  -mixing sequence. In addition, by Theorem
-mixing sequence. In addition, by Theorem  in Wu and Jiang [7] is a special case of Corollary 2.6.
in Wu and Jiang [7] is a special case of Corollary 2.6.
Proof of Theorem 2.1.
Let  . From (2.2),
. From (2.2),

By the Borel-Cantelli lemma and the Toeplitz lemma,

By  and (2.1),
and (2.1),

By (2.3),

Applying Lemma 1.2,

converges. Hence

from the Kronecker lemma. Combining (2.15)–(2.19), (2.4) holds. This completes the proof of Theorem 2.1.
Proof of Theorem 2.2.
By Lemma 1.3,

where  denote the set of all vectors
denote the set of all vectors  ,
,  such that
such that  , and
, and  are constants which do not depend on
are constants which do not depend on  and
and  Thus, in order to prove (2.6), we only need to prove that
Thus, in order to prove (2.6), we only need to prove that

When  , by Theorem 2.1, (2.21) holds. When
, by Theorem 2.1, (2.21) holds. When  we get
we get

from the elementary inequality  valid for
valid for  applied with
applied with  . Hence, in order to prove (2.21), we only need to prove that
. Hence, in order to prove (2.21), we only need to prove that

By (2.3), using Lemma 1.2, we get that

converges. By the Kronecker lemma,  Thus,
Thus,

that is,

By (2.3),

By Lemma 1.2, we have that

converges. By the Kronecker lemma,

By  and the Toeplitz lemma,
and the Toeplitz lemma,

Then combining (2.5), we obtain

Substituting (2.29) and (2.31) in (2.26), we get

Then combining (2.2) and the Borel-Cantelli lemma, (2.23) holds. This completes the proof of Theorem 2.2.
Proof of Corollary 2.3.
By Theorem 2.2, we only need to verify (2.1)–(2.3) and (2.5). From  having identically distribution, (2.7), (2.8) and
having identically distribution, (2.7), (2.8) and  (2.5) holds automatically.
(2.5) holds automatically.
Since

by the Toeplitz lemma,

That is,(2.1) holds.
By (2.7),

That is, (2.2) holds.
Similarly,

That is, (2.3) holds. This completes proof of Corollary 2.3.
Proof of Theorem 2.5.
Similar to the proof of Theorem 2.2, by Lemma 1.3, in order to prove (2.12), we only need to prove that

Let  then
then

(i) When  , by (2.10) and (2.11), in order to prove
, by (2.10) and (2.11), in order to prove  we only need to prove that
we only need to prove that

By (2.9) and Lemma 1.2,

converges. By the Kronecker lemma, (2.39) holds.
-
(ii)
When
 , by (2.9) and the Kronecker lemma,
, by (2.9) and the Kronecker lemma,

By (2.10) and the Borel-Cantelli lemma,

Hence, combining (2.39), (2.37) holds. This completes the proof of Theorem 2.5.
Proof of Corollary 2.6.
Let  . We can easy to verify (2.9)–(2.11). By Theorem 2.5, Corollary 2.6 holds.
. We can easy to verify (2.9)–(2.11). By Theorem 2.5, Corollary 2.6 holds.
References
Bradley RC: On the spectral density and asymptotic normality of weakly dependent random fields. Journal of Theoretical Probability 1992,5(2):355–373. 10.1007/BF01046741
Bryc W, Smoleński W: Moment conditions for almost sure convergence of weakly correlated random variables. Proceedings of the American Mathematical Society 1993,119(2):629–635. 10.1090/S0002-9939-1993-1149969-7
Goldie CM, Greenwood PE: Variance of set-indexed sums of mixing random variables and weak convergence of set-indexed processes. The Annals of Probability 1986,14(3):817–839. 10.1214/aop/1176992440
Yang SC: Some moment inequalities for partial sums of random variables and their application. Chinese Science Bulletin 1998,43(17):1823–1826.
Wu QY: Some convergence properties for
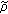 -mixing sequences. Journal of Engineering Mathematics 2001,18(3):58–64.
-mixing sequences. Journal of Engineering Mathematics 2001,18(3):58–64.Wu QY: Convergence for weighted sums of
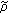 -mixing random sequences. Mathematica Applicata 2002,15(1):1–4.
-mixing random sequences. Mathematica Applicata 2002,15(1):1–4.Wu QY, Jiang YY: Some strong limit theorems for
 -mixing sequences of random variables. Statistics & Probability Letters 2008,78(8):1017–1023. 10.1016/j.spl.2007.09.061
-mixing sequences of random variables. Statistics & Probability Letters 2008,78(8):1017–1023. 10.1016/j.spl.2007.09.061Peligrad M, Gut A: Almost-sure results for a class of dependent random variables. Journal of Theoretical Probability 1999,12(1):87–104. 10.1023/A:1021744626773
Gan SX: Almost sure convergence for
 -mixing random variable sequences. Statistics & Probability Letters 2004,67(4):289–298. 10.1016/j.spl.2003.12.011
-mixing random variable sequences. Statistics & Probability Letters 2004,67(4):289–298. 10.1016/j.spl.2003.12.011Utev S, Peligrad M: Maximal inequalities and an invariance principle for a class of weakly dependent random variables. Journal of Theoretical Probability 2003,16(1):101–115. 10.1023/A:1022278404634
Wang YB, Yang Y, Zhou HY: A random functional central limit theorem for processes of product sums of linear processes generated by martingale differences. Chinese Annals of Mathematics B 2003,24(4):449–456. 10.1142/S025295990300044X
Jamison B, Orey S, Pruitt W: Convergence of weighted averages of independent random variables. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete 1965, 4: 40–44. 10.1007/BF00535481
Chen XR, Zhu L-C, Fang K-T: Almost sure convergence of weighted sums. Statistica Sinica 1996,6(2):499–507.
Acknowledgments
The authors are very grateful to the referees and the editors for their valuable comments and some helpful suggestions that improved the clarity and readability of the paper. This work was supported by the National Natural Science Foundation of China (10661006), the Support Program of the New Century Guangxi China Ten-hundred-thousand Talents Project (2005214), and the Guangxi, China Science Foundation (0991081).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wu, Q., Jiang, Y. Some Strong Limit Theorems for Weighted Product Sums of  -Mixing Sequences of Random Variables.
J Inequal Appl 2009, 174768 (2009). https://doi.org/10.1155/2009/174768
-Mixing Sequences of Random Variables.
J Inequal Appl 2009, 174768 (2009). https://doi.org/10.1155/2009/174768
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/174768
 , by (2.9) and the Kronecker lemma,
, by (2.9) and the Kronecker lemma,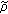 -mixing sequences. Journal of Engineering Mathematics 2001,18(3):58–64.
-mixing sequences. Journal of Engineering Mathematics 2001,18(3):58–64.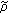 -mixing random sequences. Mathematica Applicata 2002,15(1):1–4.
-mixing random sequences. Mathematica Applicata 2002,15(1):1–4. -mixing sequences of random variables. Statistics & Probability Letters 2008,78(8):1017–1023. 10.1016/j.spl.2007.09.061
-mixing sequences of random variables. Statistics & Probability Letters 2008,78(8):1017–1023. 10.1016/j.spl.2007.09.061 -mixing random variable sequences. Statistics & Probability Letters 2004,67(4):289–298. 10.1016/j.spl.2003.12.011
-mixing random variable sequences. Statistics & Probability Letters 2004,67(4):289–298. 10.1016/j.spl.2003.12.011