- Research Article
- Open access
- Published:
On Convergence of 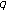 -Series Involving
-Series Involving 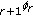 Basic Hypergeometric Series
Basic Hypergeometric Series
Journal of Inequalities and Applications volume 2009, Article number: 170526 (2009)
Abstract
We use inequality technique and the terminating case of the  -binomial formula to give some results on convergence of
-binomial formula to give some results on convergence of  -series involving
-series involving  basic hypergeometric series. As an application of the results, we discuss the convergence for special Thomae
basic hypergeometric series. As an application of the results, we discuss the convergence for special Thomae  -integral.
-integral.
1. Introduction

-Series, which are also called basic hypergeometric series, play a very important role in many fields, such as affine root systems, Lie algebras and groups, number theory, orthogonal polynomials and physics. Convergence of a  -series is an important problem in the study of
-series is an important problem in the study of  -series. There are some results about it in [1–3]. For example, Ito used inequality technique to give a sufficient condition for convergence of a special
-series. There are some results about it in [1–3]. For example, Ito used inequality technique to give a sufficient condition for convergence of a special  -series called Jackson integral. In this paper, by using inequality technique, we derive the following two theorems on convergence of
-series called Jackson integral. In this paper, by using inequality technique, we derive the following two theorems on convergence of  -series involving
-series involving  basic hypergeometric series, which can be used for convergence of special Thomae
basic hypergeometric series, which can be used for convergence of special Thomae  -integral.
-integral.
2. Notations and Known Results
We recall some definitions, notations, and known results which will be used in the proofs. Throughout this paper, it is supposed that  . The
. The  -shifted factorials are defined as
-shifted factorials are defined as

We also adopt the following compact notation for multiple  -shifted factorials:
-shifted factorials:

where  is an integer or
is an integer or  .
.
The  -binomial theorem [4, 5] is
-binomial theorem [4, 5] is

When  , where
, where  denotes a nonnegative integer
denotes a nonnegative integer

Heine introduced the  basic hypergeometric series, which is defined by [4, 5]
basic hypergeometric series, which is defined by [4, 5]

3. Main Results
The main purpose of the present paper is to establish the following two theorems on convergence of  -series involving
-series involving  basic hypergeometric series.
basic hypergeometric series.
Theorem 3.1.
Suppose  ,
,  are any real numbers such that
are any real numbers such that  and
and  with
with  . Let
. Let  be any sequence of numbers. If
be any sequence of numbers. If

then the  -series
-series

converges absolutely.
Proof.
Let  and
and

It is easy to see that  is a monotone function with respect to
is a monotone function with respect to  .
.
Consequently, one has

From (3.4), one knows

where  for
for  .
.
So, one has

It is obvious that

Multiplying both sides of (3.6) by

gives

Hence,

By using (2.4) one obtains

Substituting (3.11) into (3.10), one has

Multiplying both sides of (3.12) by  , one has
, one has

The ratio test shows that the series

is absolutely convergent. From (3.13), it is sufficient to establish that (3.2) is absolutely convergent.
Theorem 3.2.
Suppose  are any real numbers such that
are any real numbers such that  and
and  with
with  . Let
. Let  be any sequence of numbers. If
be any sequence of numbers. If

then the  -series
-series

diverges.
Proof.
Let  ,
,  and
and

It is easy to see that  is a monotone function with respect to
is a monotone function with respect to  .
.
Consequently, one has

From (3.18), one knows

where  for
for  .
.
So, one has

It is obvious that

Multiplying both sides of (3.20) by

gives

Hence,

By using (2.4) one obtains

Substituting (3.25) into (3.24), one has

Multiplying both sides of (3.26) by  , one has
, one has

Since

By hypothesis

therefore, in both cases there exists a integer  such that
such that 

So, one can conclude that

Now, from (3.27) and (3.31)

Thereby, (3.16) diverges.
We want to point out that some  -integral can be written as (3.2) or (3.16). So, the results obtained here can be used to discuss the convergence of
-integral can be written as (3.2) or (3.16). So, the results obtained here can be used to discuss the convergence of  -integrals.
-integrals.
4. Some Applications
In [6, 7], Thomae defined the  -integral on the interval
-integral on the interval  by
by

The right side of (4.1) corresponds to use a Riemann sum with partition points  Jackson [8] extended Thomae
Jackson [8] extended Thomae  -integral via
-integral via

In this section, we use the theorems derived in this paper to discuss two examples of the convergence for Thomae  -integral. We have the following theorems.
-integral. We have the following theorems.
Theorem 4.1.
Let  be any real numbers such that
be any real numbers such that  and
and  with
with  . If
. If  , then the Thomae
, then the Thomae  -integral
-integral

converges absolutely.
Proof.
By the definition of Thomae  -integral (4.1), one has
-integral (4.1), one has

Using Theorem 3.1 and noticing,

one knows that (4.3) converges absolutely.
Theorem 4.2.
Let  ,
,  be any real numbers such that
be any real numbers such that  and
and  with
with  . If
. If  , then the Thomae
, then the Thomae  -integral
-integral

diverges.
Proof.
By the definition of Thomae  -integral (4.1), one has
-integral (4.1), one has

Using Theorem 3.2 and noticing,

one knows that (4.6) diverges.
References
Ito M: Convergence and asymptotic behavior of Jackson integrals associated with irreducible reduced root systems. Journal of Approximation Theory 2003,124(2):154–180. 10.1016/j.jat.2003.08.006
Wang M: An inequality for
 and its applications. Journal of Mathematical Inequalities 2007,1(3):339–345.
and its applications. Journal of Mathematical Inequalities 2007,1(3):339–345.Wang M: Two inequalities for
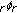 and applications. Journal of Inequalities and Applications 2008, 2008:-6.
and applications. Journal of Inequalities and Applications 2008, 2008:-6.Andrews GE: The Theory of Partitions, Encyclopedia of Mathematics and Its Applications. Volume 2. Addison-Wesley, Reading, Mass, USA; 1976:xiv+255.
Gasper G, Rahman M: Basic Hypergeometric Series, Encyclopedia of Mathematics and Its Applications. Volume 35. Cambridge University Press, Cambridge, Mass, USA; 1990:xx+287.
Thomae J: Beiträge zur Theorie der durch die Heine'sche Reihe darstellbaren Funktionen. Journal für die reine und angewandte Mathematik 1869, 70: 258–281.
Thomae J: Les séries Heinéennes supérieures, ou les séries de la forme
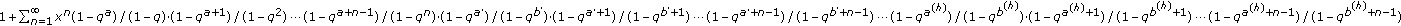 . Annali di Matematica Pura ed Applicata 1870, 4: 105–138.
. Annali di Matematica Pura ed Applicata 1870, 4: 105–138.Jackson FH: On
 -definite integrals. Quarterly Journal of Pure and Applied Mathematics 1910, 50: 101–112.
-definite integrals. Quarterly Journal of Pure and Applied Mathematics 1910, 50: 101–112.
Acknowledgment
The authors would like to express deep appreciation to the referees for the helpful suggestions. In particular, the authors thank the referees for help to improve the presentation of the paper. Mingjin Wang was supported by STF of Jiangsu Polytechnic University.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, M., Zhao, X. On Convergence of 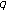 -Series Involving
-Series Involving 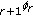 Basic Hypergeometric Series.
J Inequal Appl 2009, 170526 (2009). https://doi.org/10.1155/2009/170526
Basic Hypergeometric Series.
J Inequal Appl 2009, 170526 (2009). https://doi.org/10.1155/2009/170526
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/170526
 and its applications. Journal of Mathematical Inequalities 2007,1(3):339–345.
and its applications. Journal of Mathematical Inequalities 2007,1(3):339–345.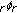 and applications. Journal of Inequalities and Applications 2008, 2008:-6.
and applications. Journal of Inequalities and Applications 2008, 2008:-6.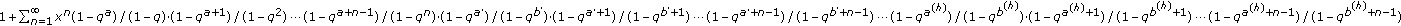 . Annali di Matematica Pura ed Applicata 1870, 4: 105–138.
. Annali di Matematica Pura ed Applicata 1870, 4: 105–138. -definite integrals. Quarterly Journal of Pure and Applied Mathematics 1910, 50: 101–112.
-definite integrals. Quarterly Journal of Pure and Applied Mathematics 1910, 50: 101–112.