- Research Article
- Open access
- Published:
A New General Integral Operator Defined by Al-Oboudi Differential Operator
Journal of Inequalities and Applications volume 2009, Article number: 158408 (2009)
Abstract
We define a new general integral operator using Al-Oboudi differential operator. Also we introduce new subclasses of analytic functions. Our results generalize the results of Breaz, Güney, and Sălăgean.
1. Introduction
Let  denote the class of functions of the form
denote the class of functions of the form

which are analytic in the open unit disk  , and
, and  .
.
For  , Al-Oboudi [1] introduced the following operator:
, Al-Oboudi [1] introduced the following operator:



If  is given by (1.1), then from (1.3) and (1.4) we see that
is given by (1.1), then from (1.3) and (1.4) we see that

with  .
.
Remark 1.1.
When  , we get Sălăgean's differential operator [2].
, we get Sălăgean's differential operator [2].
Now we introduce new classes  and
and  as follows.
as follows.
A function  is in the classes
is in the classes  , where
, where  ,
,  ,
,  ,
,  , if and only if
, if and only if

or equivalently

for all  .
.
A function  is in the classs
is in the classs  , where
, where  ,
,  ,
,  ,
,  , if and only if
, if and only if

for all  .
.
We note that  if and only if
if and only if  .
.
Remark 1.2.
-
(i)
For
 and
and  , we have the classes
, we have the classes 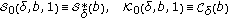 (1.9)
(1.9)
introduced by Frasin [3].
-
(ii)
For
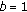 and
and 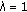 , we have the class
, we have the class  (1.10)
(1.10)
of  -starlike functions of order
-starlike functions of order  defined by Sălăgean [2].
defined by Sălăgean [2].
-
(iii)
In particular, the classes
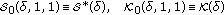 (1.11)
(1.11)
are the classes of starlike functions of order  and convex functions of order
and convex functions of order  in
in  , respectively.
, respectively.
-
(iv)
Furthermore, the classes
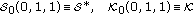 (1.12)
(1.12)
are familiar classes of starlike and convex functions in  , respectively.
, respectively.
-
(v)
For
 , we get
, we get 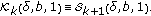 (1.13)
(1.13)
Let us introduce the new subclasses  ,
,  and
and  ,
,  as follows.
as follows.
A function  is in the class
is in the class  if and only if
if and only if  satisfies
satisfies

or equivalently

where  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
A function  is in the class
is in the class  if and only if
if and only if  satisfies
satisfies

where  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
We note that  if and only if
if and only if  .
.
Remark 1.3.
-
(i)
For
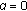 , we have
, we have  (1.17)
(1.17)
-
(ii)
For
 and
and 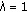 , we have the class
, we have the class  (1.18)
(1.18)
of  -uniform starlike functions of order
-uniform starlike functions of order  and type
and type  , [4].
, [4].
-
(iii)
For
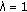 , we have
, we have  (1.19)
(1.19)
-
(iv)
For
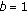 and
and 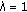 , we have
, we have 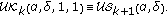 (1.20)
(1.20)
Geometric Interpretation

and  if and only if
if and only if  and
and  , respectively, take all the values in the conic domain
, respectively, take all the values in the conic domain  which is included in the right-half plane such that
which is included in the right-half plane such that

From elementary computations we see that  represents the conic sections symmetric about the real axis. Thus
represents the conic sections symmetric about the real axis. Thus  is an elliptic domain for
is an elliptic domain for  , a parabolic domain for
, a parabolic domain for  , a hyperbolic domain for
, a hyperbolic domain for  and a right-half plane
and a right-half plane  for
for  .
.
A function  is in the class
is in the class  if and only if
if and only if  satisfies
satisfies

where  ,
,  ,
,  ,
,  .
.
A function  is in the class
is in the class  if and only if
if and only if  satisfies
satisfies

where  ,
,  ,
,  ,
,  .
.
We note that  if and only if
if and only if  .
.
Remark 1.4.
-
(i)
For
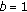 and
and  , we have the classes
, we have the classes 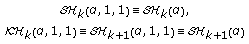 (1.24)
(1.24)
defined in [5].
-
(ii)
For
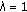 , we have
, we have  (1.25)
(1.25)
-
D.
Breaz and N. Breaz [6] introduced and studied the integral operator
 (1.26)
(1.26)
where  and
and  for all
for all  .
.
By using the Al-Oboudi differential operator, we introduce the following integral operator. So we generalize the integral operator  .
.
Definition 1.5.
Let ,
,  , and
, and ,
,  . One defines the integral operator
. One defines the integral operator

where  and
and  is the Al-Oboudi differential operator.
is the Al-Oboudi differential operator.
Remark 1.6.
In Definition 1.5, if we set
2. Main Results
The following lemma will be required in our investigation.
Lemma 2.1.
For the integral operator  , defined by (1.27), one has
, defined by (1.27), one has

Proof.
By (1.27), we get

Also, using (1.3) and (1.4), we obtain

On the other hand, from (2.2) and (2.3), we find


Thus by (2.2) and (2.4), we can write

Finally, we obtain

which is the desired result.
Theorem 2.2.
Let ,
,  ,
, 
 , and
, and  ,
,  . Also suppose that
. Also suppose that

If 
 , then the integral operator
, then the integral operator  , defined by (1.27), is in the class
, defined by (1.27), is in the class  , where
, where

Proof.
Since 
 , by (1.14) we have
, by (1.14) we have

for all  . By (2.1), we get
. By (2.1), we get

So, (2.10) and (2.11) give us

for all  . Hence, we obtain
. Hence, we obtain  , where
, where  .
.
Corollary 2.3.
Let  ,
,  ,
, 
 , and
, and  . Also suppose that
. Also suppose that

If 
 , then the integral operator
, then the integral operator  , defined by (1.27), is in the class
, defined by (1.27), is in the class  , where
, where  is defined as in (2.9).
is defined as in (2.9).
Proof.
In Theorem 2.2, we consider  .
.
From Corollary 2.3, we immediately get Corollary 2.4.
Corollary 2.4.
Let  ,
,  ,
, 
 , and
, and  . Also suppose that
. Also suppose that

If 
 , then the integral operator
, then the integral operator  , defined by (1.27), is in the class
, defined by (1.27), is in the class  .
.
Remark 2.5.
If we set  in Corollary 2.4, then we have [7, Theorem 1]. So Corollary 2.4 is an extension of Theorem 1.
in Corollary 2.4, then we have [7, Theorem 1]. So Corollary 2.4 is an extension of Theorem 1.
Corollary 2.6.
Let
 and
and  ,
,  . Also suppose that
. Also suppose that

If 
 , then the integral operator
, then the integral operator  , defined by (1.27), is in the class
, defined by (1.27), is in the class  , where
, where

Proof.
In Theorem 2.2, we consider  .
.
Corollary 2.7.
Let
 and
and  . Also suppose that
. Also suppose that

If 
 , then the integral operator
, then the integral operator  , defined by (1.27), is in the class
, defined by (1.27), is in the class  , where
, where  is defined as in (2.16).
is defined as in (2.16).
Proof.
In Corollary 2.6, we consider  .
.
Corollary 2.8 readily follows from Corollary 2.7.
Corollary 2.8.
Let
 , and
, and  . Also suppose that
. Also suppose that

If 
 , then the integral operator
, then the integral operator  , defined by (1.27), is in the class
, defined by (1.27), is in the class  .
.
Remark 2.9.
If we set  in Corollary 2.8, then we have [7, Corollary 1].
in Corollary 2.8, then we have [7, Corollary 1].
Theorem 2.10.
Let ,
,  ,
, 
 and
and  ,
,  . Also suppose that
. Also suppose that

If 
 , then the integral operator
, then the integral operator  , defined by (1.27), is in the class
, defined by (1.27), is in the class  , where
, where  is defined as in (2.9).
is defined as in (2.9).
Proof.
The proof is similar to the proof of Theorem 2.2.
Corollary 2.11.
Let ,
,  ,
, 
 and
and  . Also suppose that
. Also suppose that

If 
 , then the integral operator
, then the integral operator  , defined by (1.27), is in the class
, defined by (1.27), is in the class  , where
, where  is defined as in (2.9).
is defined as in (2.9).
Proof.
In Theorem 2.10, we consider  .
.
Remark 2.12.
If we set  in Corollary 2.11, then we have [7, Theorem 2].
in Corollary 2.11, then we have [7, Theorem 2].
Corollary 2.13.
Let and
and  ,
,  . Also suppose that
. Also suppose that

If 
 , then the integral operator
, then the integral operator  , defined by (1.27), is in the class
, defined by (1.27), is in the class  , where
, where  is defined as in (2.16).
is defined as in (2.16).
Proof.
In Theorem 2.10, we consider  .
.
Corollary 2.14.
Let and
and  . Also suppose that
. Also suppose that

If 
 , then the integral operator
, then the integral operator  , defined by (1.27), is in the class
, defined by (1.27), is in the class  , where
, where  is defined as in (2.16).
is defined as in (2.16).
Proof.
In Corollary 2.13, we consider  .
.
Remark 2.15.
If we set  in Corollary 2.14, then we have [7, Corollary 2].
in Corollary 2.14, then we have [7, Corollary 2].
Theorem 2.16.
Let ,
,  ,
,  and
and  ,
,  . Also suppose that
. Also suppose that

If 
 , then the integral operator
, then the integral operator  , defined by (1.27), is in the class
, defined by (1.27), is in the class  .
.
Proof.
Since 
 , by (1.14) we have
, by (1.14) we have

for all  .
.
On the other hand, from (2.1), we obtain

Considering (1.16) with the above equality, we find

for all  . This completes proof.
. This completes proof.
Corollary 2.17.
Let ,
,  ,
,  , and
, and  . Also suppose that
. Also suppose that

If 
 , then the integral operator
, then the integral operator  , defined by (1.27), is in the class
, defined by (1.27), is in the class  .
.
Proof.
In Theorem 2.16, we consider  .
.
Remark 2.18.
If we set  in Corollary 2.17, then we have [7, Theorem 3].
in Corollary 2.17, then we have [7, Theorem 3].
Theorem 2.19.
Let ,
,  , and
, and  . Also suppose that
. Also suppose that

If 
 , then the integral operator
, then the integral operator  , defined by (1.27), is in the class
, defined by (1.27), is in the class  .
.
Proof.
Since 
 , by (1.22) we have
, by (1.22) we have

for all  . Considering this inequality and (2.1), we obtain
. Considering this inequality and (2.1), we obtain

for all  . Hence by (1.23), we have
. Hence by (1.23), we have  .
.
Corollary 2.20.
Let and
and  . Also suppose that
. Also suppose that

If 
 , then the integral operator
, then the integral operator  , defined by (1.27), is in the class
, defined by (1.27), is in the class  .
.
Proof.
In Theorem 2.19, we consider  .
.
Remark 2.21.
If we set  in Corollary 2.20, then we have [7, Theorem 4].
in Corollary 2.20, then we have [7, Theorem 4].
Theorem 2.22.
Let ,
,  and
and  . Also suppose that
. Also suppose that

If 
 , then the integral operator
, then the integral operator  , defined by (1.27), is in the class
, defined by (1.27), is in the class  .
.
Proof.
Since 
 , by (1.22) we have
, by (1.22) we have

for all  . Considering this inequality and (2.1), we obtain
. Considering this inequality and (2.1), we obtain

for all  . Hence, by (1.8), we have
. Hence, by (1.8), we have  .
.
Corollary 2.23.
Let and
and  . Also suppose that
. Also suppose that

If 
 , then the integral operator
, then the integral operator  , defined by (1.27), is in the class
, defined by (1.27), is in the class  .
.
Proof.
In Theorem 2.22, we consider  .
.
Remark 2.24.
If we set  in Corollary 2.23, then we have [7, Theorem 5].
in Corollary 2.23, then we have [7, Theorem 5].
References
Al-Oboudi FM: On univalent functions defined by a generalized Sălăgean operator. International Journal of Mathematics and Mathematical Sciences 2004,2004(27):1429–1436. 10.1155/S0161171204108090
Sălăgean GŞ: Subclasses of univalent functions. In Complex Analysis-Fifth Romanian-Finnish Seminar, Part 1 (Bucharest, 1981), Lecture Notes in Mathematics. Volume 1013. Springer, Berlin, Germany; 1983:362–372. 10.1007/BFb0066543
Frasin BA: Family of analytic functions of complex order. Acta Mathematica. Academiae Paedagogicae Nyíregyháziensis 2006,22(2):179–191.
Magdaş I: , Doctoral thesis. University "Babeş-Bolyai", Cluj-Napoca, Romania; 1999.
Acu M: Subclasses of convex functions associated with some hyperbola. Acta Universitatis Apulensis 2006, (12):3–12.
Breaz D, Breaz N: Two integral operators. Studia Universitatis Babeş-Bolyai. Mathematica 2002,47(3):13–19.
Breaz D, Güney HÖ, Sălăgean GŞ: A new general integral operator. Tamsui Oxford Journal of Mathematical Sciences. Accepted Tamsui Oxford Journal of Mathematical Sciences. Accepted
Bulut S: Some properties for an integral operator defined by Al-Oboudi differential operator. Journal of Inequalities in Pure and Applied Mathematics 2008.,9(4, article 115):
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Bulut, S. A New General Integral Operator Defined by Al-Oboudi Differential Operator. J Inequal Appl 2009, 158408 (2009). https://doi.org/10.1155/2009/158408
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/158408
 and
and  , we have the classes
, we have the classes 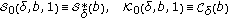
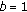 and
and 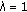 , we have the class
, we have the class 
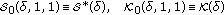
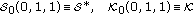
 , we get
, we get 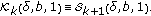
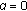 , we have
, we have 
 and
and 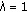 , we have the class
, we have the class 
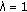 , we have
, we have 
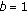 and
and 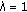 , we have
, we have 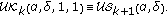
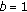 and
and  , we have the classes
, we have the classes 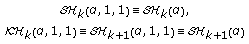
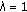 , we have
, we have 



 and
and  , then we have the integral operator defined by (1.26).
, then we have the integral operator defined by (1.26).
 , then we have [
, then we have [