- Research Article
- Open access
- Published:
Note on the 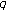 -Extension of Barnes' Type Multiple Euler Polynomials
-Extension of Barnes' Type Multiple Euler Polynomials
Journal of Inequalities and Applications volume 2009, Article number: 136532 (2009)
Abstract
We construct the  -Euler numbers and polynomials of higher order, which are related to Barnes' type multiple Euler polynomials. We also derive many properties and formulae for our
-Euler numbers and polynomials of higher order, which are related to Barnes' type multiple Euler polynomials. We also derive many properties and formulae for our  -Euler polynomials of higher order by using the multiple integral equations on
-Euler polynomials of higher order by using the multiple integral equations on  .
.
1. Introduction
Let  be a fixed odd prime number. Throughout this paper, symbols
be a fixed odd prime number. Throughout this paper, symbols  ,
,  ,
,  , and
, and  will denote the ring of rational integers, the ring of
will denote the ring of rational integers, the ring of  -adic integers, the field of
-adic integers, the field of  -adic rational numbers, and the completion of algebraic closure of
-adic rational numbers, and the completion of algebraic closure of  , respectively. Let
, respectively. Let  be the set of natural numbers and
be the set of natural numbers and  . Let
. Let  be the normalized exponential valuation of
be the normalized exponential valuation of  with
with  . When one talks of
. When one talks of  -extension,
-extension,  is variously considered as an indeterminate, a complex number
is variously considered as an indeterminate, a complex number  or a
or a  -adic number
-adic number  . If
. If  one normally assumes
one normally assumes  If
If  then one normally assumes
then one normally assumes  We use the following notations:
We use the following notations:

Let  a fixed positive odd integer with
a fixed positive odd integer with  . For
. For  , we set
, we set

where  lies in
lies in  . The fermionic
. The fermionic  -adic
-adic  -measures on
-measures on  are defined as
are defined as

(see [5]).
We say that  is a uniformly differentiable function at a point
is a uniformly differentiable function at a point  and write
and write  , if the difference quotients
, if the difference quotients  have a limit
have a limit  as
as  . For
. For  , let us begin with expression
, let us begin with expression

which represents a  -analogue of Riemann sums for
-analogue of Riemann sums for  in the fermionic sense (see [4, 5]). The integral of
in the fermionic sense (see [4, 5]). The integral of  on
on  is defined by the limit of these sums (as
is defined by the limit of these sums (as  ) if this limit exists. The fermionic invariant
) if this limit exists. The fermionic invariant  -adic
-adic  -integral of function
-integral of function  is defined as
is defined as

Note that if  in
in  , then
, then

The Barnes' type Euler polynomials are considered as follows:

where  (cf. [7]).
(cf. [7]).
From (1.5), we can derive the fermionic invariant integral on  as follows:
as follows:

For  , let
, let  , one has
, one has

By (1.9), we see that

From (1.10), we note that

In the view point of (1.11), we try to study the  -extension of Barnes' type Euler polynomials by using the
-extension of Barnes' type Euler polynomials by using the  -extension of fermionic
-extension of fermionic  -adic invariant integral on
-adic invariant integral on  .
.
The purpose of this paper is to construct the  -Euler numbers and polynomials of higher order, which are related to Barnes' type multiple Euler numbers and polynomials. Also, we give many properties and formulae for our
-Euler numbers and polynomials of higher order, which are related to Barnes' type multiple Euler numbers and polynomials. Also, we give many properties and formulae for our  -Euler polynomials of higher order. Finally, we give the generating function for these
-Euler polynomials of higher order. Finally, we give the generating function for these  -Euler polynomials of higher order.
-Euler polynomials of higher order.
2. Barnes' Type Multiple 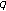 -Euler Polynomials
-Euler Polynomials
Let  . For
. For  and
and  with
with  , we define the Barnes' type multiple
, we define the Barnes' type multiple  -Euler polynomials as follows:
-Euler polynomials as follows:

where

In the special case  ,
,  are called the Barnes' type multiple
are called the Barnes' type multiple  -Euler numbers. From (2.1), one has
-Euler numbers. From (2.1), one has

Therefore, we obtain the following theorem.
Theorem 2.1.
Let  and
and  . For
. For  , one has
, one has

By (1.7), we easily see that

From (1.7), we can derive

By (2.6), one has

Hence we obtain the following theorem.
Theorem 2.2.
For  and
and  , one has
, one has

It is not difficult to show that the following integral equation is satisfied:

where  with
with  . By (2.9), we obtain the following theorem.
. By (2.9), we obtain the following theorem.
Theorem 2.3.
Let  and
and  . For
. For  with
with  , one has
, one has

For the special case  in Theorem 2.3, one has
in Theorem 2.3, one has

By (2.1), (2.3), and (2.9), we obtain the following corollary.
Corollary 2.4.
For  and
and  , one has
, one has

From (2.3), we note that

where  is an odd positive integer. By (2.13), we obtain the following theorem.
is an odd positive integer. By (2.13), we obtain the following theorem.
Theorem 2.5.
For  with
with  (mod
(mod ), one has
), one has

Remark 2.6.
Let

From (2.4), we can easily derive the following equation:

By differentiating both sides of (2.16) with respect to  and comparing coefficients on both sides, one has
and comparing coefficients on both sides, one has

The inversion formula of Equation (2.4) at  is given by
is given by

Thus, one has

References
Acikgoz M, Simsek Y: On multiple interpolation functions of the Nörlund-type
 -Euler polynomials. Abstract and Applied Analysis 2009, Article ID 382574, vol. 2009:-14 Pages.
-Euler polynomials. Abstract and Applied Analysis 2009, Article ID 382574, vol. 2009:-14 Pages.Cangul IN, Kurt V, Ozden H, Simsek Y: On the higher-order
 -
- -genocchi numbers. Advanced Studies in Contemporary Mathematics 2009,vol. 19 no.(1):pp.39–57.
-genocchi numbers. Advanced Studies in Contemporary Mathematics 2009,vol. 19 no.(1):pp.39–57.Govil NK, Gupta V: Convergence of
 -Meyer-König-Zeller-Durrmeyer operators. Advanced Studies in Contemporary Mathematics 2009, vol 19: pp. 97–108.
-Meyer-König-Zeller-Durrmeyer operators. Advanced Studies in Contemporary Mathematics 2009, vol 19: pp. 97–108.Kim T:
 -Volkenborn integration. Russian Journal of Mathematical Physics 2002,vol. 9 no.(3):pp. 288–299.
-Volkenborn integration. Russian Journal of Mathematical Physics 2002,vol. 9 no.(3):pp. 288–299.Kim T: Some identities on the
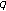 -Euler polynomials of higher order and
-Euler polynomials of higher order and  -stirling numbers by the fermionic
-stirling numbers by the fermionic  -adic integral on
-adic integral on  . Russian Journal of Mathematical Physics 2010., vol 17:
. Russian Journal of Mathematical Physics 2010., vol 17:Kim Y-H, Kim W, Ryoo CS: On the twisted
 -Euler zeta function associated with twisted
-Euler zeta function associated with twisted 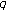 -Euler numbers. Proceedings of the Jangjeon Mathematical Society 2009,vol. 12no. (1):pp. 93–100.
-Euler numbers. Proceedings of the Jangjeon Mathematical Society 2009,vol. 12no. (1):pp. 93–100.Simsek Y, Kim T, Pyung IS: Barnes' type multiple Changhee
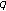 -zeta functions. Advanced Studies in Contemporary Mathematics 2005,vol. 10no. (2):pp. 121–129.
-zeta functions. Advanced Studies in Contemporary Mathematics 2005,vol. 10no. (2):pp. 121–129.
Acknowledgment
This paper was supported by Konkuk University (2009).
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jang, L., Kim, T., Kim, YH. et al. Note on the 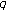 -Extension of Barnes' Type Multiple Euler Polynomials.
J Inequal Appl 2009, 136532 (2009). https://doi.org/10.1155/2009/136532
-Extension of Barnes' Type Multiple Euler Polynomials.
J Inequal Appl 2009, 136532 (2009). https://doi.org/10.1155/2009/136532
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/136532
 (see [
(see [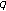 -Euler Polynomials
-Euler Polynomials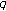 -Euler polynomials. Abstract and Applied Analysis 2009, Article ID 382574, vol. 2009:-14 Pages.
-Euler polynomials. Abstract and Applied Analysis 2009, Article ID 382574, vol. 2009:-14 Pages. -
- -genocchi numbers. Advanced Studies in Contemporary Mathematics 2009,vol. 19 no.(1):pp.39–57.
-genocchi numbers. Advanced Studies in Contemporary Mathematics 2009,vol. 19 no.(1):pp.39–57. -Meyer-König-Zeller-Durrmeyer operators. Advanced Studies in Contemporary Mathematics 2009, vol 19: pp. 97–108.
-Meyer-König-Zeller-Durrmeyer operators. Advanced Studies in Contemporary Mathematics 2009, vol 19: pp. 97–108.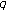 -Volkenborn integration. Russian Journal of Mathematical Physics 2002,vol. 9 no.(3):pp. 288–299.
-Volkenborn integration. Russian Journal of Mathematical Physics 2002,vol. 9 no.(3):pp. 288–299.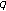 -Euler polynomials of higher order and
-Euler polynomials of higher order and  -stirling numbers by the fermionic
-stirling numbers by the fermionic  -adic integral on
-adic integral on  . Russian Journal of Mathematical Physics 2010., vol 17:
. Russian Journal of Mathematical Physics 2010., vol 17: -Euler zeta function associated with twisted
-Euler zeta function associated with twisted 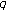 -Euler numbers. Proceedings of the Jangjeon Mathematical Society 2009,vol. 12no. (1):pp. 93–100.
-Euler numbers. Proceedings of the Jangjeon Mathematical Society 2009,vol. 12no. (1):pp. 93–100. -zeta functions. Advanced Studies in Contemporary Mathematics 2005,vol. 10no. (2):pp. 121–129.
-zeta functions. Advanced Studies in Contemporary Mathematics 2005,vol. 10no. (2):pp. 121–129.