- Research Article
- Open access
- Published:
An Interchangeable Theorem of 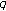 -Integral
-Integral
Journal of Inequalities and Applications volume 2009, Article number: 135693 (2009)
Abstract
We give a sufficient condition for the interchangeability of the order of sum and  -integral by using inequality technique. As the application of the theorem, some interesting results on the hypergeometric series are obtained.
-integral by using inequality technique. As the application of the theorem, some interesting results on the hypergeometric series are obtained.
1. Introduction and Some Lemmas

-series, which are also called basic hypergeometric series, plays a very important role in many fields, such as affine root systems, Lie algebras and groups, number theory, orthogonal polynomials, and physics. Inequality technique is one of the useful tools in the study of special functions. There are many papers about it (see [1–6]). First, we recall some definitions, notations, and known results which will be used in this paper. Throughout this paper, it is supposed that  . The
. The  -shifted factorials are defined as
-shifted factorials are defined as

We also adopt the following compact notation for multiple  -shifted factorial:
-shifted factorial:

where  is an integer or
is an integer or  .
.
The  -binomial theorem [2] tells us that
-binomial theorem [2] tells us that

Replace  with
with  , and
, and  with
with  and then set
and then set  , we get
, we get

Heine [2] introduced the basic hypergeometric series  , which is defined by
, which is defined by

Thomae [7] defined the  -integral on interval
-integral on interval  by
by

provided that the series converges.
Fubini's theorem. Suppose that  is absolutely summary, that is
is absolutely summary, that is

then

In order to prove the main result, we need to introduce two lemmas.
Lemma 1.1.
Let  be a given real number, satisfying
be a given real number, satisfying  . Then, for
. Then, for  , one has
, one has

Proof.
Let

since


is monotonous increasing function with respect to  . Hence,
. Hence,

(1.9) is proved.
Lemma 1.2.
Let  ,
,  be some real numbers, satisfying
be some real numbers, satisfying  with
with  . Then, for all nonnegative integer
. Then, for all nonnegative integer  , one has
, one has

Proof.
When  , it is obvious that (1.13) holds; when
, it is obvious that (1.13) holds; when  , for
, for  and
and  , we have
, we have

and by Lemma 1.1, we have

Consequently,

Thus, (1.13) follows. We complete the proof.
2. Main Result and Its Proof
We know that, whether the order of sum and  -integral is interchangeable is an important problem in the study of
-integral is interchangeable is an important problem in the study of  -series. We obtain following result on the interchangeability.
-series. We obtain following result on the interchangeability.
Theorem 2.1.
Let  ,
,  be some real numbers, satisfying
be some real numbers, satisfying  with
with  . Suppose real function
. Suppose real function  is
is  -integrable absolutely with
-integrable absolutely with  and series
and series  is convergent. Then
is convergent. Then

Proof.
Using (1.13) and (1.6), we have

Since, the series  is convergent, the series
is convergent, the series

is absolutely convergent. Hence, by the Fubini's theorem, we have

From (2.4) and (1.6), (2.1) holds. The proof is completed.
3. Applications
As the application of Theorem 2.1, in this section, we obtain some results. First, we give following lemma.
Lemma 3.1.
Let  be a real number, satisfying
be a real number, satisfying  . Then, for all nonnegative integer
. Then, for all nonnegative integer  , one has
, one has

Proof.
By (1.3) and (1.6), we have

From (3.2), (3.1) holds.
Theorem 3.2.
Let  be two real numbers, satisfying
be two real numbers, satisfying  . Then
. Then

Proof.
By (1.6), we have

By (1.3), we have

Using Theorem 2.1, we have

By Lemma 3.1, we have

Combining (3.4)–(3.7), (3.3) holds.
In (3.5), replacing  by
by  , we obtain the following result.
, we obtain the following result.
Corollary 3.3.
Let  be some real numbers, satisfying
be some real numbers, satisfying  . Then
. Then

Corollary 3.4.
Let  be a real number. Then
be a real number. Then

Proof.
Taking  in (3.8), we have
in (3.8), we have

On the other hand, by (1.4) and Theorem 2.1, we have

which by combining with (3.10), implies (3.9).
Take  , (3.9) implies the following result.
, (3.9) implies the following result.
Corollary 3.5.
The following equation holds:

Take  , (3.9) implies the following result.
, (3.9) implies the following result.
Corollary 3.6.
The following equation holds:

Remark 3.7.
Taking  , where
, where  is positive integer, (3.9) readily yields many equations.
is positive integer, (3.9) readily yields many equations.
Corollary 3.8.
Let  be a real number, satisfying
be a real number, satisfying  . Then
. Then

Proof.
Taking  in (3.8), we have
in (3.8), we have

On the other hand, by Theorem 2.1 and set  then replace
then replace  with
with  in (1.3), we have
in (1.3), we have

Combining (3.15) and (3.16), (3.14) follows.
Theorem 3.9.
Let  be two real numbers, satisfying
be two real numbers, satisfying  . Then
. Then

Proof.
We recall the Heines transformation formula [7]

In (3.18), replacing  by
by  , respectively, (3.18) yields
, respectively, (3.18) yields

Taking the  -integral on both sides of (3.19) with respect to variable
-integral on both sides of (3.19) with respect to variable  , we have
, we have

Applying (1.5) to (3.20) yields

Applying Theorem 2.1 and Lemma 3.1 to (3.21), we have

hence,

From (3.23) and (1.5), (3.17) follows.
References
Anderson GD, Barnard RW, Richards KC, Vamanamurthy MK, Vuorinen M: Inequalities for zero-balanced hypergeometric functions. Transactions of the American Mathematical Society 1995,347(5):1713–1723. 10.2307/2154966
Gasper G, Rahman M: Basic Hypergeometric Series, Encyclopedia of Mathematics and Its Applications. Volume 35. Cambridge University Press, Cambridge, UK; 1990:xx+287.
Ito M: Convergence and asymptotic behavior of Jackson integrals associated with irreducible reduced root systems. Journal of Approximation Theory 2003,124(2):154–180. 10.1016/j.jat.2003.08.006
Wang M: An inequality for
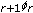 and its applications. Journal of Mathematical Inequalities 2007,1(3):339–345.
and its applications. Journal of Mathematical Inequalities 2007,1(3):339–345.Wang M: Two inequalities for
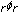 and applications. Journal of Inequalities and Applications 2008, 2008:-6.
and applications. Journal of Inequalities and Applications 2008, 2008:-6.Wang M, Ruan H: An inequality about
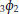 and its applications. Journal of Inequalities in Pure and Applied Mathematics 2008,9(2, article 48):-6.
and its applications. Journal of Inequalities in Pure and Applied Mathematics 2008,9(2, article 48):-6.Rogers LJ: On a three-fold symmetry in the elements of Heine's series. Proceedings of the London Mathematical Society 1893, 24: 171–179.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ruan, H. An Interchangeable Theorem of 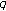 -Integral.
J Inequal Appl 2009, 135693 (2009). https://doi.org/10.1155/2009/135693
-Integral.
J Inequal Appl 2009, 135693 (2009). https://doi.org/10.1155/2009/135693
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/135693
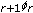 and its applications. Journal of Mathematical Inequalities 2007,1(3):339–345.
and its applications. Journal of Mathematical Inequalities 2007,1(3):339–345.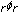 and applications. Journal of Inequalities and Applications 2008, 2008:-6.
and applications. Journal of Inequalities and Applications 2008, 2008:-6.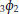 and its applications. Journal of Inequalities in Pure and Applied Mathematics 2008,9(2, article 48):-6.
and its applications. Journal of Inequalities in Pure and Applied Mathematics 2008,9(2, article 48):-6.