- Research Article
- Open access
- Published:
Generalized Strongly Nonlinear Implicit Quasivariational Inequalities
Journal of Inequalities and Applications volume 2009, Article number: 124953 (2009)
Abstract
We prove an existence theorem for solution of generalized strongly nonlinear implicit quasivariational inequality problems and convergence of iterative sequences with errors, involving Lipschitz continuous, generalized pseudocontractive and generalized  -pseudocontractive mappings in Hilbert spaces.
-pseudocontractive mappings in Hilbert spaces.
1. Introduction
Variational inequality was initially studied by Stampacchia [1] in 1964. Since then, it has been extensively studied because of its crucial role in the study of mechanics, physics, economics, transportation and engineering sciences, and optimization and control. Thanks to its wide applications, the classical variational inequality has been well studied and generalized in various directions. For details, readers are referred to [2–5] and the references therein.
It is known that one of the most important and difficult problems in variational inequality theory is the development of an efficient and implementable approximation schemes for solving various classes of variational inequalities and variational inclusions. Recently, Huang [6–8] and Cho et al. [9] constructed some new perturbed iterative algorithms for approximation of solutions of some generalized nonlinear implicit quasi-variational inclusions (inequalities), which include many iterative algorithms for variational and quasi-variational inclusions (inequalities) as special cases. Inspired and motivated by recent research works [1, 9–19], we prove an existence theorem for solution of generalized strongly nonlinear implicit quasi-variational inequality problems and convergence of iterative sequences with errors, involving Lipschitzian, generalized pseudocontractivity and generalized  -pseudocontractive mappings in Hilbert spaces.
-pseudocontractive mappings in Hilbert spaces.
2. Preliminaries
Let  be a real Hilbert space with norm
be a real Hilbert space with norm  and inner product
and inner product  . For a nonempty closed convex subset
. For a nonempty closed convex subset  , let
, let  be the projection of
be the projection of  onto
onto  . Let
. Let  be a set valued mapping with nonempty closed convex values,
be a set valued mapping with nonempty closed convex values,  and
and  be the mappings. We consider the following problem.
be the mappings. We consider the following problem.
Find  , such that
, such that  and
and

The problem (2.1) is called the generalized strongly nonlinear implicit quasi-variational inequality problem.
Special Cases
-
(i)
If
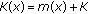 , for all
, for all  , where
, where 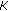 is a nonempty closed convex subset of
is a nonempty closed convex subset of  and
and  is a mapping, then the problem (2.1) is equivalent to finding
is a mapping, then the problem (2.1) is equivalent to finding  such that
such that  and
and

the problem (2.2) is called generalized nonlinear quasi-variational inequality problem.
-
(ii)
If we assume
 as identity mappings, then (2.1) reduces to the problem of finding
as identity mappings, then (2.1) reduces to the problem of finding 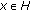 such that
such that  and
and

which is known as general implicit nonlinear quasi-variational inequality problem.
-
(iii)
If we assume
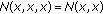 , then (2.3) reduces to the following problem of finding
, then (2.3) reduces to the following problem of finding 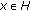 such that
such that  and
and

which is known as generalized implicit nonlinear quasi-variational inequality problem, a variant form as can be seen in [20, equation ( 2.6)].
-
(iv)
If we assume
 , then (2.4) reduces to the following problem of finding
, then (2.4) reduces to the following problem of finding  such that
such that  and
and

The problem (2.5) is called the generalized strongly nonlinear implicit quasi-variational inequality problem, considered and studied by Cho et al. [9].
-
(v)
If
 ,
,  an identity mapping, then (2.5) is equivalent to finding
an identity mapping, then (2.5) is equivalent to finding 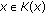 such that
such that

Problem (2.6) is called generalized strongly nonlinear quasi-variational inequality problem, see special cases of Cho et al. [9].
-
(vi)
If
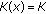 ,
, 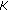 a nonempty closed convex subset of
a nonempty closed convex subset of  and
and  for all
for all  , where
, where 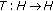 a nonlinear mapping, then the problem (2.6) is equivalent to finding
a nonlinear mapping, then the problem (2.6) is equivalent to finding 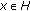 such that
such that

which is a nonlinear variational inequality, considered by Verma [17].
-
(vii)
If
 , for all
, for all  , then (2.7) reduces to the following problem for finding
, then (2.7) reduces to the following problem for finding  such that
such that

which is a classical variational inequality considered by [1, 4, 5].
Now, we recall the following iterative process due to Ishikawa [13], Mann [14], Noor [15] and Liu [21].
-
(1)
Let
 be a nonempty convex subset of
be a nonempty convex subset of  and
and 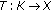 a mapping. The sequence
a mapping. The sequence  , defined by
, defined by 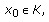 (29)
(29)


, is called the three-step iterative process, where  ,
,  , and
, and  are three real sequences in [ 0,1] satisfying some conditions.
are three real sequences in [ 0,1] satisfying some conditions.
-
(2)
In particular, if
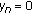 for all
for all 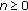 , then
, then 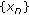 , defined by
, defined by  (211)
(211)

, is called the Ishikawa iterative process, where  and
and  are two real sequences in [ 0,1] satisfying some conditions.
are two real sequences in [ 0,1] satisfying some conditions.
-
(3)
In particular, if
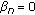 for all
for all 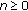 , then
, then  defined by
defined by  (212)
(212)
for  , is called the Mann iterative process.
, is called the Mann iterative process.
Recently Liu [21] introduced the concept of three-step iterative process with errors which is the generalization of Ishikawa [13] and Mann [14] iterative process, for nonlinear strongly accretive mappings as follows.
-
(4)
For a nonempty subset
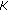 of a Banach spaces
of a Banach spaces  and a mapping
and a mapping 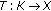 , the sequence
, the sequence  , defined by
, defined by 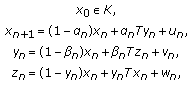 (213)
(213)

, is called the three-step iterative process with errors. Here  ,
,  and
and  are three summable sequences in
are three summable sequences in  (i.e.,
(i.e.,  ,
,  and
and  ), and
), and  ,
,  and
and  are three sequences in [ 0,1] satisfying certain restrictions.
are three sequences in [ 0,1] satisfying certain restrictions.
-
(5)
In particular, if
 for
for  and
and 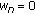 . The sequence
. The sequence 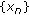 defined by
defined by


, is called the Ishikawa iterative process with errors. Here  and
and  are two summable sequences in
are two summable sequences in  (i.e.,
(i.e.,  and
and  ;
;  and
and  are two sequences in [ 0,1] satisfying certain restrictions.
are two sequences in [ 0,1] satisfying certain restrictions.
-
(6)
In particular, if
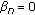 and
and  for all
for all  . The sequence
. The sequence  defined by
defined by


for  , is called the Mann iterative process with errors, where
, is called the Mann iterative process with errors, where  is a summable sequence in
is a summable sequence in  and
and  a sequence in [ 0,1] satisfying certain restrictions.
a sequence in [ 0,1] satisfying certain restrictions.
However, in a recent paper [19] Xu pointed out that the definitions of Liu [21] are against the randomness of the errors and revised the definitions of Liu [21] as follows.
-
(7)
Let
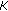 be a nonempty convex subset of a Banach space
be a nonempty convex subset of a Banach space  and
and  a mapping. For any given
a mapping. For any given  , the sequence
, the sequence 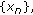 defined by
defined by


for  , is called the three-step iterative process with errors, where
, is called the three-step iterative process with errors, where  ,
,  and
and  are three bounded sequences in
are three bounded sequences in  and
and  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  and
and  are nine sequences in [ 0,1] satisfying the conditions
are nine sequences in [ 0,1] satisfying the conditions

(8) If  for
for  the sequence
the sequence  defined by
defined by

for  , is called the Ishikawa iterative process with errors, where
, is called the Ishikawa iterative process with errors, where  and
and  are two bounded sequences in
are two bounded sequences in  ,
,  ,
,  ,
,  ,
,  ,
,  and
and  are six sequences in [ 0,1] satisfying the conditions
are six sequences in [ 0,1] satisfying the conditions

(9) If  for
for  , the sequence
, the sequence  defined by
defined by

for  , is called the Mann iterative process with errors.
, is called the Mann iterative process with errors.
For our main results, we need the following lemmas.
Lemma 2.1 (see [3]).
If  is a closed convex subset and
is a closed convex subset and  a given point, then
a given point, then  satisfies the inequality
satisfies the inequality

if and only if

where  is the projection of
is the projection of  onto
onto  .
.
Lemma 2.2 (see [10]).
The mapping  defined by (2.24) is nonexpansive, that is,
defined by (2.24) is nonexpansive, that is,

Lemma 2.3 (see [10]).
If  and
and  is a closed convex subset, then for any
is a closed convex subset, then for any  , one has
, one has

Lemma 2.4 (see [21]).
Let  ,
,  and
and  be three nonnegative real sequences satisfying
be three nonnegative real sequences satisfying

Then

By Lemma 2.1, we know that the generalized strongly nonlinear implicit quasi-variational inequality (2.1) has a unique solution if and only if the mapping  by
by

has a unique fixed point, where  is a constant.
is a constant.
3. Main Results
In this section, we establish an existence theorem for solution of generalized strongly nonlinear implicit quasi-variational inequality problems and convergence of the iterative sequences generated by (2.18). First, we give some definitions.
Definition 3.1.
A mapping  is said to be generalized pseudo-contractive if there exists a constant
is said to be generalized pseudo-contractive if there exists a constant  such that
such that

It is easy to check that (3.1) is equivalent to

For  in (3.1), we get the usual concept of pseudo-contractive of
in (3.1), we get the usual concept of pseudo-contractive of  , introduced by Browder and Petryshyn [10], that is,
, introduced by Browder and Petryshyn [10], that is,

Definition 3.2.
Let  and
and  be the mappings. The mapping
be the mappings. The mapping  is said to be as follows.
is said to be as follows.
(i)Generalized pseudo-contractive with respect to  in the first argument of
in the first argument of  , if there exists a constant
, if there exists a constant  such that
such that

(ii)Lipschitz continuous with respect to the first argument of  if there exists a constant
if there exists a constant  such that
such that

In a similar way, we can define Lipschitz continuity of N with respect to the second and third arguments.
(iii) is also said to be Lipschitz continuous if there exists a constant
is also said to be Lipschitz continuous if there exists a constant  such that
such that

Definition 3.3.
Let  be the mappings. A mapping
be the mappings. A mapping  is said to be the generalized
is said to be the generalized  -pseudo-contractive with respect to the second argument of
-pseudo-contractive with respect to the second argument of  , if there exists a constant
, if there exists a constant  such that
such that

Definition 3.4.
Let  be a set-valued mapping such that for each
be a set-valued mapping such that for each  ,
,  is a nonempty closed convex subset of
is a nonempty closed convex subset of  . The projection
. The projection  is said to be Lipschitz continuous if there exists a constant
is said to be Lipschitz continuous if there exists a constant  such that
such that

Remark 3.5.
In many important applications,  has the following form:
has the following form:

where  is a single-valued mapping and
is a single-valued mapping and  a nonempty closed convex subset of
a nonempty closed convex subset of  . If
. If  is Lipschitz continuous with constant
is Lipschitz continuous with constant  , then from Lemma 2.3,
, then from Lemma 2.3,  is Lipschitz continuous with Lipschitz constant
is Lipschitz continuous with Lipschitz constant  .
.
Now, we give the main result of this paper.
Theorem 3.6.
Let  be a real Hilbert space and
be a real Hilbert space and  a set-valued mapping with nonempty closed convex values. Let
a set-valued mapping with nonempty closed convex values. Let  be the Lipschitz continuous mappings with positive constants
be the Lipschitz continuous mappings with positive constants  and
and  respectively. Let
respectively. Let  be the mapping such that
be the mapping such that  and
and  are Lipschitz continuous with positive constants
are Lipschitz continuous with positive constants  and
and  respectively. A trimapping
respectively. A trimapping  is generalized pseudo-contractive with respect to
is generalized pseudo-contractive with respect to  in the first argument of
in the first argument of  with constant
with constant  and generalized
and generalized  -pseudo-contractive with respect to
-pseudo-contractive with respect to  in the second argument of
in the second argument of  with constant
with constant  , Lipschitz continuous with respect to the first, second, and third arguments with positive constants
, Lipschitz continuous with respect to the first, second, and third arguments with positive constants  respectively. Suppose that
respectively. Suppose that  is Lipschitz continuous with constant
is Lipschitz continuous with constant  . Let
. Let  ,
,  and
and  be the three bounded sequences in
be the three bounded sequences in  and
and  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  and
and  are sequences in
are sequences in  satisfying the following conditions:
satisfying the following conditions:
(1)
(2)
(3)
If the following conditions hold:

where  and
and  .
.
Then there exists a unique  satisfying the generalized strongly nonlinear implicit quasi-variational inequality (2.1) and
satisfying the generalized strongly nonlinear implicit quasi-variational inequality (2.1) and  as
as  , where
, where  is the three-step iteration process with errors defined as follows:
is the three-step iteration process with errors defined as follows:

for  .
.
Proof.
We first prove that the generalized strongly nonlinear implicit quasi-variational inequality (2.1) has a unique solution. By Lemma 2.1, it is sufficient to prove the mapping defined by

has a unique fixed point in  .
.
Let  be two arbitrary points in
be two arbitrary points in  . From Lemma 2.2 and Lipschitz continuity of
. From Lemma 2.2 and Lipschitz continuity of  and
and  , we have
, we have

Since  is generalized pseudo-contractive with respect to
is generalized pseudo-contractive with respect to  in the first argument of
in the first argument of  and Lipschitz continuous with respect to first argument of
and Lipschitz continuous with respect to first argument of  and also
and also  is Lipschitz continuous, we have
is Lipschitz continuous, we have

Again since  is generalized
is generalized  -pseudo-contractive with respect to
-pseudo-contractive with respect to  in the second argument of
in the second argument of  and Lipschitz continuous with respect to second argument of
and Lipschitz continuous with respect to second argument of  and
and  is Lipschitz continuous, we have
is Lipschitz continuous, we have


It follows from (3.13)–(3.16) that

where

From (3.10), we know that  and so
and so  has a unique fixed point
has a unique fixed point  , which is a unique solution of the generalized strongly nonlinear implicit quasi-variational inequality (2.1).
, which is a unique solution of the generalized strongly nonlinear implicit quasi-variational inequality (2.1).
Now we prove that  converges to
converges to  . In fact, it follows from (3.11) and
. In fact, it follows from (3.11) and  that
that

From (3.17) and (3.19), it follows that

Similarly, we have

Again,

Let

Then  and
and

Similarly, we deduce from (3.21) the following:


From the above inequalities, we get

where

Since  , it follows from conditions (1) and (3) that
, it follows from conditions (1) and (3) that


Therefore,

From (3.29)-(3.31) and Lemma 2.4, we know that  converges to the solution
converges to the solution  . This completes the proof.
. This completes the proof.
Remark 3.7.
We now deduce Theorem 3.6 in the direction of Ishikawa iteration.
Theorem 3.8.
Let  be a real Hilbert space and
be a real Hilbert space and  a set-valued mapping with the nonempty closed convex values. Let
a set-valued mapping with the nonempty closed convex values. Let  and
and  be the same as in Theorem 3.6. Suppose that
be the same as in Theorem 3.6. Suppose that  is Lipschitz continuous with constant
is Lipschitz continuous with constant  . Let
. Let  and
and  be the two bounded sequences in
be the two bounded sequences in  and
and  ,
,  ,
,  ,
,  ,
,  and
and  be six sequences in
be six sequences in  satisfying the following conditions:
satisfying the following conditions:
(1)
(2)
(3)
If the following conditions holds:

Then there exists a unique  satisfying the generalized strongly nonlinear implicit quasi-variational inequality (2.1) and
satisfying the generalized strongly nonlinear implicit quasi-variational inequality (2.1) and  as
as  , where
, where  is the Ishikawa iteration process with errors defined as follows:
is the Ishikawa iteration process with errors defined as follows:

for  .
.
Remark 3.9.
We can also deduce Theorem 3.6 in the direction of (2.16).
Theorem 3.10.
Let  and
and  be the same as in Theorem 3.6. Let
be the same as in Theorem 3.6. Let  be a bounded sequence in
be a bounded sequence in  and
and  ,
,  and
and  be three sequences in
be three sequences in  satisfying the following conditions:
satisfying the following conditions:
(1) for
for  ,
,
(2) ,
,
(3) and
and 
If the conditions of (3.10) hold, then there exists a unique  satisfying the generalized strongly nonlinear implicit quasi-variational inequality (2.1) and
satisfying the generalized strongly nonlinear implicit quasi-variational inequality (2.1) and  as
as  , where
, where  is the Mann iterative process with errors defined as follows:
is the Mann iterative process with errors defined as follows:

for  .
.
Our results can be further improved in the direction of (2.25).
Theorem 3.11.
Let  be a real Hilbert space and
be a real Hilbert space and  a set-valued mapping with nonempty closed convex values. Let
a set-valued mapping with nonempty closed convex values. Let  be the Lipschitz continuous mapping with respect to positive constants
be the Lipschitz continuous mapping with respect to positive constants  and
and  respectively. Let
respectively. Let  be the mapping such that
be the mapping such that  and
and  be Lipschitz continuous with respect to positive constants
be Lipschitz continuous with respect to positive constants  and
and  respectively. A trimapping
respectively. A trimapping  is generalized pseudo-contractive with respect to map
is generalized pseudo-contractive with respect to map  in first argument of
in first argument of  with constant
with constant  and generalized
and generalized  -pseudo-contractive with respect to
-pseudo-contractive with respect to  in the second argument of
in the second argument of  with constant
with constant  , Lipschitz continuous with respect to first, second, and third arguments with positive constants
, Lipschitz continuous with respect to first, second, and third arguments with positive constants  , respectively. Suppose that
, respectively. Suppose that  is a Lipschitz continuous with positive constant
is a Lipschitz continuous with positive constant  . Let
. Let  ,
,  and
and  be three bounded sequences in
be three bounded sequences in  satisfying the conditions (1)–(3) of Theorem 3.6. If the conditions of (3.10) hold for
satisfying the conditions (1)–(3) of Theorem 3.6. If the conditions of (3.10) hold for  , then there exists a unique
, then there exists a unique  satisfying (2.2) and
satisfying (2.2) and  as
as  , where
, where  is the three step iteration process with errors defined as follows:
is the three step iteration process with errors defined as follows:

for  .
.
Now, we deduce Theorem 3.6 for three step iterative process in terms of (2.10).
Theorem 3.12.
Let  and
and  be the same as in Theorem 3.6. Let
be the same as in Theorem 3.6. Let  ,
,  ,
,  ,
,  ,
,  and
and  be six sequences in
be six sequences in  satisfying conditions:
satisfying conditions:
(1) for
for 
(2) ,
,
(3)
If the conditions of (3.10) hold, then there exists  satisfying (2.1) and
satisfying (2.1) and  as
as  , where the three-step iteration process
, where the three-step iteration process  is defined by
is defined by

for  .
.
Next, we state the results in terms of iterations (2.10) and (2.25).
Theorem 3.13.
Let  and
and  be the same as in the Theorem 3.11. Let
be the same as in the Theorem 3.11. Let  ,
,  ,
,  ,
,  ,
,  and
and  be six sequences in
be six sequences in  satisfying conditions (1)–(3) of Theorem 3.6. If the conditions of (3.10) hold for
satisfying conditions (1)–(3) of Theorem 3.6. If the conditions of (3.10) hold for  , then there exists
, then there exists  satisfying the generalized strongly nonlinear implicit quasi-variational inequality (2.2) and
satisfying the generalized strongly nonlinear implicit quasi-variational inequality (2.2) and  as
as  , where the three-step iteration process
, where the three-step iteration process  is defined by
is defined by

for  .
.
Remark 3.14.
Theorem 3.13 can also be deduce for Ishikawa and Mann iterative process.
References
Stampacchia G: Formes bilinéaires coercitives sur les ensembles convexes. Comptes Rendus de l'Académie des Sciences 1964, 258: 4413–4416.
Bensoussan A, Lions J-L: Impulse Control and Quasi-Variational Inequalities. Gauthier-Villars, Montrouge, France; 1984:xiv+684.
Chang SS: Variational Inequality and Complementarity Problem Theory with Application. Shanghai Scientific and Technological Literature Publishing House, Shanghai, China; 1991.
Giannessi F, Maugeri A: Variational Inequalities and Network Equilibrium Problems. Plenum Press, New York, NY, USA; 1995.
Glowinski R, Lions JL, Tremolieres R: Numerical Analysis of Variational Inequalities, Studies in Mathematics and Its Applications. North-Holland, Amsterdam, The Netherlands; 1981:xxix+776.
Huang N-J: Mann and Ishikawa type perturbed iterative algorithms for generalized nonlinear implicit quasi-variational inclusions. Computers & Mathematics with Applications 1998,35(10):1–7. 10.1016/S0898-1221(98)00066-2
Huang N-J: On the generalized implicit quasi-variational inequalities. Journal of Mathematical Analysis and Applications 1997, 216: 197–210. 10.1006/jmaa.1997.5671
Huang N-J: A new completely general class of variational inclusions with noncompact valued mappings. Computers & Mathematics with Applications 1998,35(10):9–14. 10.1016/S0898-1221(98)00067-4
Cho YJ, Kim JH, Huang N-J, Kang SM: Ishikawa and Mann iterative processes with errors for generalized strongly nonlinear implicit quasi-variational inequalities. Publicationes Mathematicae Debrecen 2001,58(4):635–649.
Browder FE, Petryshyn WV: Construction of fixed points of nonlinear mappings in Hilbert space. Journal of Mathematical Analysis and Applications 1967, 20: 197–228. 10.1016/0022-247X(67)90085-6
Chidume CE, Ofoedu EU: A new iteration process for finite families of generalized Lipschitz pseudo-contractive and generalized Lipschitz accretive mappings. Nonlinear Analysis: Theory, Methods & Applications 2008,69(4):1200–1207. 10.1016/j.na.2007.06.022
Ding XP: Perturbed proximal point algorithms for generalized quasivariational inclusions. Journal of Mathematical Analysis and Applications 1997,210(1):88–101. 10.1006/jmaa.1997.5370
Ishikawa S: Fixed points by a new iteration method. Proceedings of the American Mathematical Society 1974,44(1):147–150. 10.1090/S0002-9939-1974-0336469-5
Mann WR: Mean value methods in iteration. Proceedings of the American Mathematical Society 1953, 4: 506–510. 10.1090/S0002-9939-1953-0054846-3
Noor MA: New approximation schemes for general variational inequalities. Journal of Mathematical Analysis and Applications 2000,251(1):217–229. 10.1006/jmaa.2000.7042
Song Y: On a Mann type implicit iteration process for continuous pseudo-contractive mappings. Nonlinear Analysis: Theory, Methods & Applications 2007,67(11):3058–3063. 10.1016/j.na.2006.09.059
Verma RU: Generalized pseudo-contractions and nonlinear variational inequalities. Publicationes Mathematicae Debrecen 1998,53(1–2):23–28.
Xiang CH: Fixed point theorem for generalized
 -pseudocontractive mappings. Nonlinear Analysis: Theory, Methods & Applications 2009,70(6):2277–2279. 10.1016/j.na.2008.03.006
-pseudocontractive mappings. Nonlinear Analysis: Theory, Methods & Applications 2009,70(6):2277–2279. 10.1016/j.na.2008.03.006Xu Y: Ishikawa and Mann iterative processes with errors for nonlinear strongly accretive operator equations. Journal of Mathematical Analysis and Applications 1998,224(1):91–101. 10.1006/jmaa.1998.5987
Fang YA-P, Huang N-J, Kang JIM, Cho YJE: Generalized nonlinear implicit quasivariational inclusions. Journal of Inequalities and Applications 2005,2005(3):261–275. 10.1155/JIA.2005.261
Liu Q: Convergence theorems of the sequence of iterates for asymptotically demicontractive and hemicontractive mappings. Nonlinear Analysis: Theory, Methods & Applications 1996,26(11):1835–1842. 10.1016/0362-546X(94)00351-H
Acknowledgment
The authors thank the editor Professor R. U. Verma and anonymous referees for their valuable useful suggestions that improved the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Salahuddin, Ahmad, M.K. Generalized Strongly Nonlinear Implicit Quasivariational Inequalities. J Inequal Appl 2009, 124953 (2009). https://doi.org/10.1155/2009/124953
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/124953
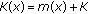 , for all
, for all  , where
, where 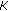 is a nonempty closed convex subset of
is a nonempty closed convex subset of  and
and  is a mapping, then the problem (2.1) is equivalent to finding
is a mapping, then the problem (2.1) is equivalent to finding  such that
such that  and
and as identity mappings, then (2.1) reduces to the problem of finding
as identity mappings, then (2.1) reduces to the problem of finding 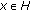 such that
such that  and
and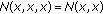 , then (2.3) reduces to the following problem of finding
, then (2.3) reduces to the following problem of finding 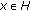 such that
such that  and
and , then (2.4) reduces to the following problem of finding
, then (2.4) reduces to the following problem of finding  such that
such that  and
and ,
,  an identity mapping, then (2.5) is equivalent to finding
an identity mapping, then (2.5) is equivalent to finding 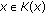 such that
such that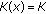 ,
, 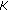 a nonempty closed convex subset of
a nonempty closed convex subset of  and
and  for all
for all  , where
, where 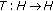 a nonlinear mapping, then the problem (2.6) is equivalent to finding
a nonlinear mapping, then the problem (2.6) is equivalent to finding 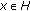 such that
such that , for all
, for all  , then (2.7) reduces to the following problem for finding
, then (2.7) reduces to the following problem for finding  such that
such that be a nonempty convex subset of
be a nonempty convex subset of  and
and 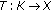 a mapping. The sequence
a mapping. The sequence  , defined by
, defined by 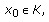
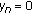 for all
for all 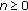 , then
, then 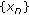 , defined by
, defined by 
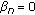 for all
for all 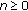 , then
, then  defined by
defined by 
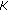 of a Banach spaces
of a Banach spaces  and a mapping
and a mapping 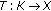 , the sequence
, the sequence  , defined by
, defined by 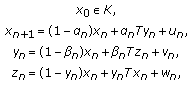
 for
for  and
and 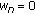 . The sequence
. The sequence 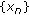 defined by
defined by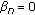 and
and  for all
for all  . The sequence
. The sequence  defined by
defined by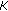 be a nonempty convex subset of a Banach space
be a nonempty convex subset of a Banach space  and
and  a mapping. For any given
a mapping. For any given  , the sequence
, the sequence 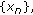 defined by
defined by -pseudocontractive mappings. Nonlinear Analysis: Theory, Methods & Applications 2009,70(6):2277–2279. 10.1016/j.na.2008.03.006
-pseudocontractive mappings. Nonlinear Analysis: Theory, Methods & Applications 2009,70(6):2277–2279. 10.1016/j.na.2008.03.006