- Research Article
- Open access
- Published:
Some Inequalities of the Grüss Type for the Numerical Radius of Bounded Linear Operators in Hilbert Spaces
Journal of Inequalities and Applications volume 2008, Article number: 763102 (2010)
Abstract
Some inequalities of the Grüss type for the numerical radius of bounded linear operators in Hilbert spaces are established.
1. Introduction
Let  be a complex Hilbert space. The numerical range of an operator
be a complex Hilbert space. The numerical range of an operator  is the subset of the complex numbers
is the subset of the complex numbers  given by [1, page 1]:
given by [1, page 1]:

The numerical radius of an operator
of an operator  on
on  is given by [1, page 8]:
is given by [1, page 8]:

It is well known that  is a norm on the Banach algebra
is a norm on the Banach algebra  of all bounded linear operators
of all bounded linear operators  This norm is equivalent to the operator norm. In fact, the following more precise result holds [1, page 9].
This norm is equivalent to the operator norm. In fact, the following more precise result holds [1, page 9].
Theorem 1.1 (equivalent norm).
For any  one has
one has

For other results on numerical radius (see [2, Chapter 11]).
We recall some classical results involving the numerical radius of two linear operators 
The following general result for the product of two operators holds [1, page 37].
Theorem 1.2.
If  are two bounded linear operators on the Hilbert space
are two bounded linear operators on the Hilbert space  then
then

In the case that  then
then

The following results are also well known [1, page 38].
Theorem 1.3.
If  is a unitary operator that commutes with another operator
is a unitary operator that commutes with another operator  then
then

If  is an isometry and
is an isometry and  then (1.6) also holds true.
then (1.6) also holds true.
We say that  and
and  double commute, if
double commute, if  and
and 
The following result holds [1, page 38].
Theorem 1.4 (double commute).
If the operators  and
and  double commute, then
double commute, then

As a consequence of the above, one has [1, page 39] the following.
Corollary 1.5.
Let  be a normal operator commuting with
be a normal operator commuting with  Then
Then

For other results and historical comments on the above (see [1, pages 39–41]). For more results on the numerical radius, see [2].
In the recent survey paper [3], we provided other inequalities for the numerical radius of the product of two operators. We list here some of the results.
Theorem 1.6.
Let  be two bounded linear operators on the Hilbert space
be two bounded linear operators on the Hilbert space  then
then

respectively.
If more information regarding one of the operators is available, then the following results may be stated as well.
Theorem 1.7.
Let  be two bounded linear operators on
be two bounded linear operators on  , and
, and  is invertible such that, for a given
is invertible such that, for a given 

Then

respectively.
Motivated by the natural questions that arise, in order to compare the quantity  with other expressions comprising the norm or the numerical radius of the involved operators
with other expressions comprising the norm or the numerical radius of the involved operators  and
and  (or certain expressions constructed with these operators), we establish in this paper some natural inequalities of the form
(or certain expressions constructed with these operators), we establish in this paper some natural inequalities of the form

or

where  and
and  are specified and desirably simple constants (depending on the given operators
are specified and desirably simple constants (depending on the given operators  and
and 
Applications in providing upper bounds for the non-negative quantities

and the superunitary quantities

are also given.
2. Numerical Radius Inequalities of Grüss Type
For the complex numbers  and the bounded linear operator
and the bounded linear operator  , we define the following transform:
, we define the following transform:

where by  we denote the adjoint of
we denote the adjoint of  .
.
We list some properties of the transform  that are useful in the following.
that are useful in the following.
(i)For any  and
and  we have
we have

-
(ii)
The operator
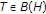 is normal, if and only if
is normal, if and only if  for each
for each 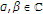 .
.
We recall that a bounded linear operator  on the complex Hilbert space
on the complex Hilbert space  is called accretive, if
is called accretive, if  , for any
, for any 
Utilizing the following identity

that holds for any scalars  and any vector
and any vector  with
with  we can give a simple characterization result that is useful in the following.
we can give a simple characterization result that is useful in the following.
Lemma 2.1.
For  and
and  the following statements are equivalent.
the following statements are equivalent.
(i)The transform is accretive.
is accretive.
(ii)The transform is accretive.
is accretive.
(iii)One has the norm inequality

or, equivalently,

Remark 2.2.
In order to give examples of operators  and numbers
and numbers  such that the transform
such that the transform  is accretive, it suffices to select a bounded linear operator
is accretive, it suffices to select a bounded linear operator  and the complex numbers
and the complex numbers  with the property that
with the property that  , and by choosing
, and by choosing  and
and  we observe that
we observe that  satisfies (2.4), that is,
satisfies (2.4), that is,  is accretive.
is accretive.
The following results compare the quantities  and
and  provided that some information about the transforms
provided that some information about the transforms  and
and  are available, where
are available, where  .
.
Theorem 2.3.
Let  and
and  be such that the transforms
be such that the transforms  and
and  are accretive, then
are accretive, then

Proof.
Since  and
and  are accretive, then, on making use of Lemma 2.1, we have that
are accretive, then, on making use of Lemma 2.1, we have that

for any 
Now, we make use of the following Grüss type inequality for vectors in inner product spaces obtained by the author in [4] (see also [5] or [6, page 43]).
Let  be an inner product space over the real or complex number field
be an inner product space over the real or complex number field  ,
,  and
and  such that
such that

or equivalently,

then

Applying (2.10) for  , and
, and  we deduce
we deduce

for any  which is an inequality of interest in itself.
which is an inequality of interest in itself.
Observing that

then by (2.10), we deduce the inequality

for any  On taking the supremum over
On taking the supremum over  in (2.13), we deduce the desired result (2.6).
in (2.13), we deduce the desired result (2.6).
The following particular case provides an upper bound for the nonnegative quantity  when some information about the operator
when some information about the operator  is available.
is available.
Corollary 2.4.
Let  and
and  be such that the transform
be such that the transform  is accretive, then
is accretive, then

Proof.
Follows on applying Theorem 2.3 above for the choice  taking into account that
taking into account that  is accretive implies that
is accretive implies that  is the same and
is the same and 
Remark 2.5.
Let  and
and  be such that the transform
be such that the transform  is accretive. Then
is accretive. Then

A sufficient simple condition for  to be accretive is that
to be accretive is that  is a self-adjoint operator on
is a self-adjoint operator on  and such that
and such that  in the partial operator order of
in the partial operator order of 
The following result may be stated as well.
Theorem 2.6.
Let  and
and  be such that
be such that  and the transforms
and the transforms  are accretive, then
are accretive, then

respectively.
Proof.
With the assumptions (2.8) (or, equivalently, (2.9) in the proof of Theorem 2.3) and if  then
then

The first inequality has been established in [7] (see [6, page 62]) while the second one can be obtained in a canonical manner from the reverse of the Schwarz inequality given in [8]. The details are omitted.
Applying (2.10) for  , and
, and  we deduce
we deduce

for any  which are of interest in themselves.
which are of interest in themselves.
A similar argument to that in the proof of Theorem 2.3 yields the desired inequalities (2.16). The details are omitted.
Corollary 2.7.
Let  and
and  be such that
be such that  and the transform
and the transform  is accretive, then
is accretive, then

respectively.
The proof is obvious from Theorem 2.6 on choosing  and the details are omitted.
and the details are omitted.
Remark 2.8.
Let  and
and  be such that the transform
be such that the transform  is accretive. Then, on making use of Corollary 2.7, we may state the following simpler results:
is accretive. Then, on making use of Corollary 2.7, we may state the following simpler results:

respectively. These two inequalities were obtained earlier by the author using a different approach (see [9]).
Problem 1.
Find general examples of bounded linear operators realizing the equality case in each of inequalities (2.6), (2.16), respectively.
3. Some Particular Cases of Interest
The following result is well known in the literature (see, e.g., [10]):

for each positive integer  and any operator
and any operator 
The following reverse inequalities for  can be stated.
can be stated.
Proposition 3.1.
Let  and
and  be such that the transform
be such that the transform  is accretive, then
is accretive, then

Proof.
On applying inequality (2.11) from Theorem 2.3 for the choice  we get the following inequality of interest in itself:
we get the following inequality of interest in itself:

for any  Since obviously,
Since obviously,

then by (3.3), we get

for any  Taking the supremum over
Taking the supremum over  in (3.5), we deduce the desired result (3.2).
in (3.5), we deduce the desired result (3.2).
Remark 3.2.
Let  and
and  be such that the transform
be such that the transform  is accretive. Then
is accretive. Then

If  in the partial operator order of
in the partial operator order of  then (3.6) is valid.
then (3.6) is valid.
Finally, we also have the following proposition.
Proposition 3.3.
Let  and
and  be such that
be such that  and the transform
and the transform  is accretive, then
is accretive, then

respectively.
Proof.
On applying inequality (2.18) from Theorem 2.6 for the choice  we get the following inequality of interest in itself:
we get the following inequality of interest in itself:

for any 
Now, on making use of a similar argument to the one in the proof of Proposition 3.1, we deduce the desired results (3.7). The details are omitted.
Remark 3.4.
Let  and
and  be such that the transform
be such that the transform  is accretive. Then, on making use of Proposition 3.3, we may state the following simpler results:
is accretive. Then, on making use of Proposition 3.3, we may state the following simpler results:

respectively.
References
Gustafson KE, Rao DKM: Numerical Range: The Field of Values of Linear Operators and Matrices, Universitext. Springer, New York, NY, USA; 1997:xiv+189.
Halmos PR: A Hilbert Space Problem Book, Graduate Texts in Mathematics. Volume 19. 2nd edition. Springer, New York, NY, USA; 1982:xvii+369.
Dragomir SS: A survey of some recent inequalities for the norm and numerical radius of operators in Hilbert spaces. Banach Journal of Mathematical Analysis 2007,1(2):154–175.
Dragomir SS: A generalization of Grüss's inequality in inner product spaces and applications. Journal of Mathematical Analysis and Applications 1999,237(1):74–82. 10.1006/jmaa.1999.6452
Dragomir SS: Some Grüss type inequalities in inner product spaces. Journal of Inequalities in Pure and Applied Mathematics 2003,4(2, article 42):1–10.
Dragomir SS: Advances in Inequalities of the Schwarz, Grüss and Bessel Type in Inner Product Spaces. Nova Science, Hauppauge, NY, USA; 2005:viii+249.
Dragomir SS: Reverses of Schwarz, triangle and Bessel inequalities in inner product spaces. Journal of Inequalities in Pure and Applied Mathematics 2004,5(3, article 76):1–18.
Dragomir SS: Reverses of the Schwarz inequality generalising a Klamkin-McLenaghan result. Bulletin of the Australian Mathematical Society 2006,73(1):69–78. 10.1017/S0004972700038636
Dragomir SS: Reverse inequalities for the numerical radius of linear operators in Hilbert spaces. Bulletin of the Australian Mathematical Society 2006,73(2):255–262. 10.1017/S0004972700038831
Pearcy C: An elementary proof of the power inequality for the numerical radius. The Michigan Mathematical Journal 1966,13(3):289–291.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Dragomir, S.S. Some Inequalities of the Grüss Type for the Numerical Radius of Bounded Linear Operators in Hilbert Spaces. J Inequal Appl 2008, 763102 (2010). https://doi.org/10.1155/2008/763102
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/763102
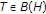 is normal, if and only if
is normal, if and only if  for each
for each 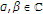 .
.