- Research Article
- Open access
- Published:
Generic Well-Posedness for a Class of Equilibrium Problems
Journal of Inequalities and Applications volume 2008, Article number: 581917 (2008)
Abstract
We study a class of equilibrium problems which is identified with a complete metric space of functions. For most elements of this space of functions (in the sense of Baire category), we establish that the corresponding equilibrium problem possesses a unique solution and is well-posed.
1. Introduction
The study of equilibrium problems has recently been a rapidly growing area of research. See, for example, [1–3] and the references mentioned therein.
Let  be a complete metric space. In this paper, we consider the following equilibrium problem:
be a complete metric space. In this paper, we consider the following equilibrium problem:

where  belongs to a complete metric space of functions
belongs to a complete metric space of functions  defined below. In this paper, we show that for most elements of this space of functions
defined below. In this paper, we show that for most elements of this space of functions  (in the sense of Baire category) the equilibrium problem (P) possesses a unique solution. In other words, the problem (P) possesses a unique solution for a generic (typical) element of
(in the sense of Baire category) the equilibrium problem (P) possesses a unique solution. In other words, the problem (P) possesses a unique solution for a generic (typical) element of  [4–6].
[4–6].
Set

Clearly,  is a complete metric space.
is a complete metric space.
Denote by  the set of all continuous functions
the set of all continuous functions  such that
such that

We equip the set  with the uniformity determined by the base
with the uniformity determined by the base

where  . It is clear that the space
. It is clear that the space  with this uniformity is metrizable (by a metric
with this uniformity is metrizable (by a metric  ) and complete.
) and complete.
Denote by  the set of all
the set of all  for which the following properties hold.
for which the following properties hold.
(P1) For each  , there exists
, there exists  such that
such that  for all
for all  .
.
(P2) For each  , there exists
, there exists  such that
such that  for all
for all  satisfying
satisfying  .
.
Clearly,  is a closed subset of
is a closed subset of  . We equip the space
. We equip the space  with the metric
with the metric  and consider the topological subspace
and consider the topological subspace  with the relative topology.
with the relative topology.
For each  and each subset
and each subset  , put
, put

For each  and each
and each  , set
, set

Assume that the following property holds.
(P3) There exists a positive number  such that for each
such that for each  and each pair of real numbers
and each pair of real numbers  satisfying
satisfying  , there is
, there is  such that
such that 
In this paper, we will establish the following result.
Theorem 1.1.
There exists a set  which is a countable intersection of open everywhere dense subsets of
which is a countable intersection of open everywhere dense subsets of  such that for each
such that for each  , the following properties hold:
, the following properties hold:
-
(i)
there exists a unique
 such that
such that 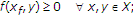 (1.6)
(1.6)
-
(ii)
for each
 , there are
, there are  and a neighborhood
and a neighborhood  of
of 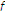 in
in  such that for each
such that for each  and each
and each 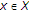 satisfying
satisfying  , the inequality
, the inequality  holds.
holds.
In other words, for a generic (typical)  , the problem (P) is well-posed [7–9].
, the problem (P) is well-posed [7–9].
2. An Auxiliary Density Result
Lemma 2.1.
Let  and
and  . Then there exist
. Then there exist  and
and  such that
such that  and
and  for all
for all  .
.
Proof.
By (P1) there is  such that
such that

Set

For each  , there is
, there is  such that
such that

For each  , there is
, there is  such that
such that

For each  , there is
, there is  such that
such that

For each  , set
, set

For any  , put
, put

and for any  , put
, put

Clearly,  is an open covering of
is an open covering of  . Since any metric space is paracompact, there is a continuous locally finite partition of unity
. Since any metric space is paracompact, there is a continuous locally finite partition of unity  subordinated to the covering
subordinated to the covering  . Namely, for any
. Namely, for any  ,
,  is a continuous function and there exist
is a continuous function and there exist  such that
such that  and that
and that

Define

Clearly,  is well defined, continuous, and satisfies
is well defined, continuous, and satisfies

Let  . Then
. Then

Assume that  and that
and that  . Then
. Then

If  , then in view of (2.5), (2.6), and (2.13),
, then in view of (2.5), (2.6), and (2.13),  , a contradiction (see (2.12)). Then
, a contradiction (see (2.12)). Then  , and by (2.7),
, and by (2.7),

Since this equality holds for any  satisfying
satisfying  , it follows from (2.10) that
, it follows from (2.10) that

for all  .
.
Relations (2.1), (2.2), and (2.15) imply that

By (1.2), (2.7), (2.8), and (2.10)

Assume that

Then in view of (2.2) and (2.18),  Together with (2.7) and (2.10), this implies that
Together with (2.7) and (2.10), this implies that

Combined with (2.11), this implies that

for all 
Let

and assume that

Then in view of (2.22),

By (2.23) and the choice of  (see (2.3)–(2.6)),
(see (2.3)–(2.6)),  and by (2.4), (2.6), (2.7), and (2.8),
and by (2.4), (2.6), (2.7), and (2.8),

Since the inequality above holds for any  satisfying (2.22), the relation (2.10) implies that
satisfying (2.22), the relation (2.10) implies that

Together with (2.11), (2.12), and (2.15), this implies that for all 

By (2.17),  . In view of (2.16),
. In view of (2.16),  possesses (P1). Since
possesses (P1). Since  possesses (P2), it follows from (2.7), (2.8), and (2.10) that
possesses (P2), it follows from (2.7), (2.8), and (2.10) that  possesses (P2). Therefore
possesses (P2). Therefore  and Lemma 2.1 now follows from (2.16) and (2.26).
and Lemma 2.1 now follows from (2.16) and (2.26).
3. A Perturbation Lemma
Lemma 3.1.
Let  ,
,  , and let
, and let  satisfy
satisfy

Then there exist  and
and  such that
such that

and if  satisfies
satisfies  then
then  .
.
Proof.
By (P2) there is a positive number

such that

Set

Define


Clearly,  is continuous and
is continuous and

By (3.6) and (3.7),

Let  . We estimate
. We estimate  . If
. If  , then by (3.6) and (3.7),
, then by (3.6) and (3.7),

Assume that

By (3.3) and (3.11),

By (3.5), (3.6), (3.7), (3.11), and (3.12),

Together with (3.10) this implies that

Assume that  . In view of (P3) and (3.3), there is
. In view of (P3) and (3.3), there is  such that
such that

It follows from (3.15) and (3.9) that


for all  . Set
. Set

Clearly, the function  is continuous and
is continuous and

In view of (3.1), (3.18), and (3.6),

Since the function  possesses (P2), it follows from (3.9), (3.20), and (3.18) that
possesses (P2), it follows from (3.9), (3.20), and (3.18) that  possesses the property (P2). Thus
possesses the property (P2). Thus  .
.
By (3.6), (3.14), and (3.18) for all 

Assume that

If  , then by (3.6) and (3.18),
, then by (3.6) and (3.18),

and together with (3.17), this implies that

This inequality contradicts (3.22). The contradiction we have reached proves that

This completes the proof of the lemma.
4. Proof of Theorem 1.1
Denote by  the set of all
the set of all  for which there exists
for which there exists  such that
such that  for all
for all  . By Lemma 2.1,
. By Lemma 2.1,  is an everywhere dense subset of
is an everywhere dense subset of  .
.
Let  and
and  be a natural number. There exists
be a natural number. There exists  such that
such that

By Lemma 3.1, there exist  and
and  such that
such that

and the following property holds.
(P4) For each  satisfying
satisfying  the inequality
the inequality  holds.
holds.
Denote by  the open neighborhood of
the open neighborhood of  in
in  such that
such that

Assume that

By (1.3), (4.3), and (4.4),

In view of (4.5) and (P4),

Thus we have shown that the following property holds.
(P5) For each  and each
and each  satisfying (4.4), the inequality
satisfying (4.4), the inequality  holds.
holds.
Set

Clearly,  is a countable intersection of open everywhere dense subset of
is a countable intersection of open everywhere dense subset of  . Let
. Let

Choose a natural number  . There exist
. There exist  and an integer
and an integer  such that
such that

The property (P4), (4.3), and (4.9) imply that for each  satisfying
satisfying

we have

Thus we have shown that the following property holds.
(P6) For each  satisfying (4.10), the inequality
satisfying (4.10), the inequality  holds.
holds.
By (P1) there is a sequence  such that
such that

In view of (4.12) and (P6) for all large enough natural numbers  , we have
, we have

Since  is any positive number, we conclude that
is any positive number, we conclude that  is a Cauchy sequence and there exists
is a Cauchy sequence and there exists

Relations (4.12) and (4.14) imply that for all 

We have also shown that any sequence  satisfying (4.12) converges. This implies that if
satisfying (4.12) converges. This implies that if  satisfies
satisfies  for all
for all  , then
, then  . By (P6) and (4.15),
. By (P6) and (4.15),

Let  and
and  satisfy (4.4). By (P5),
satisfy (4.4). By (P5),  . Together with (4.16), this implies that
. Together with (4.16), this implies that

Theorem 1.1 is proved.
References
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. The Mathematics Student 1994,63(1–4):123–145.
Chen G-Y, Huang X, Yang X: Vector Optimization, Set-Valued and Variational Analysis. Springer, Berlin, Germany; 2005:x+306.
Long XJ, Huang N-J, Teo KL: Levitin-Polyak well-posedness for equilibrium problems with functional constraints. Journal of Inequalities and Applications 2008, 2008:-14.
Aubin J-P, Ekeland I: Applied Nonlinear Analysis. John Wiley & Sons, New York, NY, USA; 1984:xi+518.
Nitecki Z: Differentiable Dynamics. An Introduction to the Orbit Structure of Diffeomorphisms. MIT Press, Cambridge, Mass, USA; 1971:xv+282.
Zaslavski AJ: Turnpike Properties in the Calculus of Variations and Optimal Control. Springer, New York, NY, USA; 2006:xxii+395.
Ioffe AD, Zaslavski AJ: Variational principles and well-posedness in optimization and calculus of variations. SIAM Journal on Control and Optimization 2000,38(2):566–581. 10.1137/S0363012998335632
Zaslavski AJ: Generic well-posedness of optimal control problems without convexity assumptions. SIAM Journal on Control and Optimization 2000,39(1):250–280. 10.1137/S0363012998345391
Zolezzi T: Well-posedness criteria in optimization with application to the calculus of variations. Nonlinear Analysis: Theory, Methods & Applications 1995,25(5):437–453. 10.1016/0362-546X(94)00142-5
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zaslavski, A.J. Generic Well-Posedness for a Class of Equilibrium Problems. J Inequal Appl 2008, 581917 (2008). https://doi.org/10.1155/2008/581917
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/581917
 such that
such that 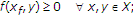
 , there are
, there are  and a neighborhood
and a neighborhood  of
of 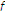 in
in  such that for each
such that for each  and each
and each 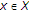 satisfying
satisfying  , the inequality
, the inequality  holds.
holds.