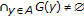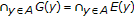- Research Article
- Open access
- Published:
Connectedness and Compactness of Weak Efficient Solutions for Set-Valued Vector Equilibrium Problems
Journal of Inequalities and Applications volume 2008, Article number: 581849 (2008)
Abstract
We study the set-valued vector equilibrium problems and the set-valued vector Hartman-Stampacchia variational inequalities. We prove the existence of solutions of the two problems. In addition, we prove the connectedness and the compactness of solutions of the two problems in normed linear space.
1. Introduction
We know that one of the important problems of vector variational inequalities and vector equilibrium problems is to study the topological properties of the set of solutions. Among its topological properties, the connectedness and the compactness are of interest. Recently, Lee et al. [1] and Cheng [2] have studied the connectedness of weak efficient solutions set for single-valued vector variational inequalities in finite dimensional Euclidean space. Gong [3–5] has studied the connectedness of the various solutions set for single-valued vector equilibrium problem in infinite dimension space. The set-valued vector equilibrium problem was introduced by Ansari et al. [6]. Since then, Ansari and Yao [7], Konnov and Yao [8], Fu [9], Hou et al. [10], Tan [11], Peng et al. [12], Ansari and Flores-Bazán [13], Lin et al. [14] and Long et al. [15] have studied the existence of solutions for set-valued vector equilibrium and set-valued vector variational inequalities problems. However, the connectedness and the compactness of the set of solutions to the set-valued vector equilibrium problem remained unstudied. In this paper, we study the existence, connectedness, and the compactness of the weak efficient solutions set for set-valued vector equilibrium problems and the set-valued vector Hartman-Stampacchia variational inequalities in normed linear space.
2. Preliminaries
Throughout this paper, let  ,
,  be two normed linear spaces, let
be two normed linear spaces, let  be a nonempty subset of
be a nonempty subset of  , let
, let  be a set-valued map, and let
be a set-valued map, and let  be a closed convex pointed cone in
be a closed convex pointed cone in  .
.
We consider the following set-valued vector equilibrium problem (SVEP): find  , such that
, such that

Definition 2.1.
Let  A vector
A vector  satisfying
satisfying

is called a weak efficient solution to the SVEP. Denote by  the set of all weak efficient solutions to the SVEP.
the set of all weak efficient solutions to the SVEP.
Let  be the topological dual space of
be the topological dual space of  . Let
. Let

be the dual cone of  .
.
Definition 2.2.
Let  . A vector
. A vector  is called an
is called an  -efficient solution to the SVEP if
-efficient solution to the SVEP if

where  means that
means that  , for all
, for all  . Denote by
. Denote by  the set of all
the set of all  -efficient solutions to the SVEP.
-efficient solutions to the SVEP.
Definition 2.3.
Let  be a nonempty convex subset in
be a nonempty convex subset in  . A set-valued map
. A set-valued map  is called to be
is called to be  -convex in its second variable if, for each fixed
-convex in its second variable if, for each fixed  , for every
, for every  ,
,  , the following property holds:
, the following property holds:

Definition 2.4.
Let  be a nonempty convex subset in
be a nonempty convex subset in  . A set-valued map
. A set-valued map  is called to be
is called to be  -concave in its first variable if, for each fixed
-concave in its first variable if, for each fixed  , for every
, for every  ,
,  , the following property holds:
, the following property holds:

Definition 2.5.
Let  be a nonempty subset of
be a nonempty subset of  . Let
. Let  be a set-valued map, where
be a set-valued map, where  is the space of all bounded linear operators from
is the space of all bounded linear operators from  into
into  (let
(let  be equipped with operator norm topology). Set
be equipped with operator norm topology). Set 
(i)Let  be a convex subset of
be a convex subset of  .
.  is said to be
is said to be  -hemicontinuous if, for every pair of points
-hemicontinuous if, for every pair of points  , the set-valued map
, the set-valued map

is lower semicontinuous at 0.
(ii)Let  .
.  is said to be
is said to be  -pseudomonotone on
-pseudomonotone on  if, for every pair of points
if, for every pair of points  ,
,  , for all
, for all  , then
, then  , for all
, for all  .
.
The definition of  -hemicontinuity was introduced by Lin et al. [14].
-hemicontinuity was introduced by Lin et al. [14].
Definition 2.6.
Let  be a Hausdorff topological vector space and let
be a Hausdorff topological vector space and let  be a nonempty set.
be a nonempty set.  is called to be a KKM map if for any finite set
is called to be a KKM map if for any finite set  the relation
the relation

holds, where  denoted the convex hull of
denoted the convex hull of  .
.
For the definition of the upper semicontinuity and lower semicontinuity, see [16].
The following FKKM theorem plays a crucial role in this paper.
Lemma 2.7.
Let  be a Hausdorff topological vector space. Let
be a Hausdorff topological vector space. Let  be a nonempty convex subset of
be a nonempty convex subset of  , and let
, and let  be a KKM map. If for each
be a KKM map. If for each  ,
,  is closed in
is closed in  , and if there exists a point
, and if there exists a point  such that
such that  is compact, then
is compact, then  .
.
By definition, we can get the following lemma.
Lemma 2.8.
Let  be a nonempty convex subset of
be a nonempty convex subset of  . Let
. Let  be a set-valued map, and let
be a set-valued map, and let  be a closed convex pointed cone. Moreover, suppose that
be a closed convex pointed cone. Moreover, suppose that  is
is  -convex in its second variable. Then, for each
-convex in its second variable. Then, for each  ,
,  is convex.
is convex.
3. Scalarization
In this section, we extend a result in [3] to set-valued map.
Theorem 3.1.
Suppose that  , and that
, and that  is a convex set for each
is a convex set for each  . Then
. Then

Proof.
It is clear that

Now we prove that

Let  . By definition,
. By definition,  , for all
, for all  . Thus
. Thus

As  is a convex pointed cone, we have
is a convex pointed cone, we have

By assumption,  is a convex set. By the separation theorem of convex sets, there exist some
is a convex set. By the separation theorem of convex sets, there exist some  , such that
, such that

By (3.6), we obtain that  and
and

Therefore,  . Hence
. Hence  . Thus we have
. Thus we have

4. Existence of The Weak Efficient Solutions
Theorem 4.1.
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  and let
and let  be a closed convex pointed cone with
be a closed convex pointed cone with  . Let
. Let  be a set-valued map with
be a set-valued map with  for all
for all  . Suppose that for each
. Suppose that for each  ,
,  is lower semicontinuous on
is lower semicontinuous on  , and that
, and that  is
is  -convex in its second variable. If there exists a nonempty compact subset
-convex in its second variable. If there exists a nonempty compact subset  of
of  , and
, and  , such that
, such that  , for all
, for all  , then, for any
, then, for any  ,
,  ,
,  ,
,  , and
, and  .
.
Proof.
Let  . Define the set-valued map
. Define the set-valued map  by
by

By assumption,  , for all
, for all  , so
, so  . We claim that
. We claim that  is a KKM map. Suppose to the contrary that there exists a finite subset
is a KKM map. Suppose to the contrary that there exists a finite subset  of
of  , and there exists
, and there exists  such that
such that  . Then
. Then  for some
for some  ,
,  , with
, with  , and
, and  , for all
, for all  . Then there exist
. Then there exist  , such that
, such that

As  is
is  -convex in its second invariable, we can get that
-convex in its second invariable, we can get that

By (4.3), we know that there exist  ,
,  , such that
, such that

Hence  . By assumption, we have
. By assumption, we have  . By (4.2), however, we have
. By (4.2), however, we have  . This is a contradiction. Thus
. This is a contradiction. Thus  is a KKM map. Now we show that for each
is a KKM map. Now we show that for each  ,
,  is closed. For any sequence,
is closed. For any sequence,  and
and  . Because
. Because  is a closed set, we have
is a closed set, we have  . By assumption, for each
. By assumption, for each  ,
,  is lower semicontinuous on
is lower semicontinuous on  , then by [16], for each fixed
, then by [16], for each fixed  , and for each
, and for each  , there exist
, there exist  , such that
, such that  . Because
. Because  , we have
, we have

Thus  . By the continuity of
. By the continuity of  and
and  , we have
, we have  . By the arbitrariness of
. By the arbitrariness of  , we have
, we have  , that is,
, that is,  . Hence
. Hence  is closed. By the assumption, we have
is closed. By the assumption, we have  , and
, and  is closed. Since
is closed. Since  is compact,
is compact,  is compact. By Lemma 2.7, we have
is compact. By Lemma 2.7, we have  . Thus there exists
. Thus there exists  . This means that
. This means that

Therefore,  . Next we show that
. Next we show that  . If
. If  , then
, then  . It follows from
. It follows from  that
that  , and by Theorem 3.1, we have
, and by Theorem 3.1, we have  .
.
Theorem 4.2.
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  and let
and let  be a closed convex pointed cone with
be a closed convex pointed cone with  . Let
. Let  . Assume that
. Assume that  is a
is a  -hemicontinuous,
-hemicontinuous,  -pseudomonotone mapping. Moreover, assume that the set-valued map
-pseudomonotone mapping. Moreover, assume that the set-valued map  defined by
defined by  is
is  -convex in its second variable. If there exists a nonempty compact subset
-convex in its second variable. If there exists a nonempty compact subset  of
of  , and
, and  , such that
, such that  , for all
, for all  , then
, then  and
and  .
.
Proof.
Let  . Define the set-valued maps
. Define the set-valued maps  ,
,  by
by

respectively. As for each  , we have
, we have  , then
, then  . The proof of the theorem is divided into four steps.
. The proof of the theorem is divided into four steps.
-
(I)
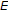
is a KKM map on
 .
.
Suppose to the contrary that there exists a finite subset  of
of  , and there exists
, and there exists  such that
such that  . Then
. Then  for some
for some  ,
,  , with
, with  , and
, and  , for all
, for all  . Then there exist
. Then there exist  such that
such that

Since  is
is  -convex in its second variable, we have
-convex in its second variable, we have

Let  , for each
, for each  . By (4.9), we know there exists
. By (4.9), we know there exists  , such that
, such that

As  , we have
, we have

While by (4.8), we have  . This is a contraction. Hence
. This is a contraction. Hence  is a KKM map on
is a KKM map on  .
.
-
(II)
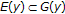
for all
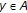 and
and 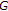 is a KKM map.
is a KKM map.
By the  -pseudomonotonicity of
-pseudomonotonicity of  , for each
, for each  , we have
, we have  . Since
. Since  is a KKM map, so is
is a KKM map, so is  .
.
-
(III)
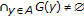
.
Now we show that for each  ,
,  is closed. Let
is closed. Let  be a sequence in
be a sequence in  such that
such that  converges to
converges to  . By the closedness of
. By the closedness of  , we have
, we have  . Since
. Since  , then for each
, then for each  , we have
, we have

As  , and the continuity of
, and the continuity of  , then for each
, then for each  , we have
, we have

Consequently,  . Hence
. Hence  is closed. By the assumption, we have
is closed. By the assumption, we have  . Then
. Then  is compact since
is compact since  is compact. By step (II), we know
is compact. By step (II), we know  is a KKM map. By Lemma 2.7,
is a KKM map. By Lemma 2.7,  .
.
-
(IV)
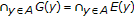
.
Because  , we have
, we have  . Now let us show that
. Now let us show that  . Let
. Let  . For each
. For each  , and each
, and each  , we have
, we have

For any  and for each fixed
and for each fixed  , define the set-valued mapping
, define the set-valued mapping  by
by

We pick a sequence  such that
such that  and set
and set  . Since
. Since  is a convex set,
is a convex set,  for each
for each  . It is clear that
. It is clear that  . Let
. Let  . We have
. We have  Since
Since  is
is  -hemicontinuous,
-hemicontinuous,  is lower semicontinuous at 0. By [16], there exist
is lower semicontinuous at 0. By [16], there exist  , such that
, such that  . As
. As  , there exist
, there exist  such that
such that  . By
. By  , we have
, we have  . By (4.14), we have
. By (4.14), we have

Since  ,
,  . Hence
. Hence  since
since  is continuous and
is continuous and  . Therefore, for any
. Therefore, for any  and for each
and for each  , we have
, we have  . Hence
. Hence  . Thus
. Thus  . This means that there exists
. This means that there exists  , for each
, for each  , we have
, we have  , for all
, for all  . It follows that
. It follows that  , thus
, thus  . By the proof of Theorem 4.1, we know
. By the proof of Theorem 4.1, we know  . Since
. Since  , we have
, we have  . The proof of the theorem is completed.
. The proof of the theorem is completed.
5. Connectedness and Compactness of The Solutions Set
In this section, we discuss the connectedness and the compactness of the weak efficient solutions set for set-valued vector equilibrium problems and the set-valued vector Hartman- Stampacchia variational inequalities in normed linear space.
Theorem 5.1.
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  , let
, let  be a closed convex pointed cone with
be a closed convex pointed cone with  , and let
, and let  be a set-valued map. Assume that the following conditions are satisfied:
be a set-valued map. Assume that the following conditions are satisfied:
(i)for each  ,
,  is lower semicontinuous on
is lower semicontinuous on  ;
;
(ii) is
is  -concave in its first variable and
-concave in its first variable and  -convex in its second variable;
-convex in its second variable;
(iii) , for all
, for all  ;
;
(iv) is a bounded subset in
is a bounded subset in  ;
;
(v)there exists a nonempty compact convex subset  of
of  , and
, and  , such that
, such that  , for all
, for all  .
.
Then  is a nonempty connected compact set.
is a nonempty connected compact set.
Proof.
We define the set-valued map  by
by

By Theorem 4.1, for each  , we have
, we have  , hence
, hence  and
and  . It is clear that
. It is clear that  is convex, so it is a connected set. Now we prove that, for each
is convex, so it is a connected set. Now we prove that, for each  ,
,  is a connected set. Let
is a connected set. Let  , we have
, we have  and
and

Because  is
is  -concave in its first variable, for each fixed
-concave in its first variable, for each fixed  , and for above
, and for above  , and
, and  , we have
, we have  since
since  is convex, and
is convex, and

Hence for each  ,
,  , there exist
, there exist  ,
,  , and
, and  , such that
, such that  . As
. As  and by (5.2), we have
and by (5.2), we have

Thus

that is  . So
. So  is convex, therefore it is a connected set.
is convex, therefore it is a connected set.
Now we show that  is upper semicontinuous on
is upper semicontinuous on  . Since
. Since  is a nonempty compact set, by [16], we only need to prove that
is a nonempty compact set, by [16], we only need to prove that  is closed. Let the sequence
is closed. Let the sequence  and
and  , where
, where  converge to
converge to  with respect to the norm topology. As
with respect to the norm topology. As  , we have
, we have

that is,  , for all
, for all  . As
. As  and
and  is compact, we have
is compact, we have  . Since for each
. Since for each  ,
,  is lower semicontinuous on
is lower semicontinuous on  , for each fixed
, for each fixed  , and each
, and each  , there exist
, there exist  , such that
, such that  . From
. From  , we have
, we have

By the continuity of  and
and  , we have
, we have

Let  . By assumption,
. By assumption,  is a bounded set in
is a bounded set in  , then there exist some
, then there exist some  , such that for each
, such that for each  , we have
, we have  . For any
. For any  , because
, because  with respect to norm topology, there exists
with respect to norm topology, there exists  , and when
, and when  , we have
, we have  . Therefore, there exists
. Therefore, there exists  , and when
, and when  , we have
, we have

Hence

Consequently, by (5.8), (5.10), we have

By (5.7), we have  . So for any
. So for any  and for each
and for each  , we have
, we have  . Hence
. Hence

This means that

Hence the graph of  is closed. Therefore,
is closed. Therefore,  is a closed map. By [16],
is a closed map. By [16],  is upper semicontinuous on
is upper semicontinuous on  . Because
. Because  is
is  -convex in its second variable, by Lemma 2.8, for each
-convex in its second variable, by Lemma 2.8, for each  ,
,  is convex. It follows from Theorem 3.1 that
is convex. It follows from Theorem 3.1 that

Thus by [17, Theorem 3.1]  is a connected set.
is a connected set.
Now, we show that  is a compact set. We first show that
is a compact set. We first show that  is a closed set. Let
is a closed set. Let  with
with  . Since
. Since  is compact,
is compact,  We claim that
We claim that  Suppose to the contrary that
Suppose to the contrary that  , then there exist some
, then there exist some  such that
such that

Thus there exists  such that
such that

Hence  is a neighborhood of
is a neighborhood of  . Since
. Since  is lower semicontinuous at
is lower semicontinuous at  , there exists some neighborhood
, there exists some neighborhood  of
of  such that
such that

Since  , there exist some
, there exist some  , and when
, and when  , we have
, we have  . By (5.17),
. By (5.17),

This contradicts  . Thus
. Thus  This means that
This means that  is a closed set. Since
is a closed set. Since  is compact and
is compact and  ,
,  is compact.
is compact.
Theorem 5.2.
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  , and let
, and let  be a closed convex pointed cone with
be a closed convex pointed cone with  . Assume that for each
. Assume that for each  ,
,  is a
is a  -hemicontinuous,
-hemicontinuous,  -pseudomonotone mapping. Moreover, assume that the set-valued map
-pseudomonotone mapping. Moreover, assume that the set-valued map  defined by
defined by  is
is  -convex in its second variable, and the set
-convex in its second variable, and the set  is a bounded set in
is a bounded set in  . If there exists a nonempty compact convex subset
. If there exists a nonempty compact convex subset  of
of  , and
, and  , such that
, such that  , for all
, for all  , then
, then  is a nonempty connected set.
is a nonempty connected set.
Proof.
We define the set-valued map  by
by

By Theorem 4.2, for each  , we have
, we have  and
and  . Hence
. Hence  and
and  . Clearly,
. Clearly,  is a convex set, hence it is a connected set. Define the set-valued maps
is a convex set, hence it is a connected set. Define the set-valued maps  ,
,  by
by

respectively. Now we prove that for each  ,
,  is a connected set. Let
is a connected set. Let  , then
, then  . By the proof of Theorem 4.2, we have
. By the proof of Theorem 4.2, we have  , so
, so  . Hence for
. Hence for  and for each
and for each  ,
,  , we have
, we have

Then, for each  ,
,  , and
, and  , we have
, we have  since
since  is convex and
is convex and

Hence  . Thus
. Thus  . Consequently, for each
. Consequently, for each  ,
,  is a convex set. Therefore, it is a connected set. The following is to prove that
is a convex set. Therefore, it is a connected set. The following is to prove that  is upper semicontinuous on
is upper semicontinuous on  . Since
. Since  is a nonempty compact set, by [16] we only need to show that
is a nonempty compact set, by [16] we only need to show that  is a closed map. Let sequence
is a closed map. Let sequence  and
and  , where
, where  converges to
converges to  with respect to the norm topology of
with respect to the norm topology of  . As
. As  , we have
, we have

Then, for each  , we have that
, we have that

By assumption, for each  ,
,  is
is  -pseudomonotone, and by (5.24), for each
-pseudomonotone, and by (5.24), for each  , for the above
, for the above  , and for each
, and for each  , we have
, we have

As  , we have
, we have  , and
, and  . As
. As  , and
, and  is compact, we have
is compact, we have  . Let
. Let  . By assumption,
. By assumption,  is a bounded set in
is a bounded set in  . Then, there exists
. Then, there exists  , such that for each
, such that for each  , we have
, we have  . For any
. For any  , because
, because  with respect to the norm topology, there exists
with respect to the norm topology, there exists  , and when
, and when  , we have
, we have  . Therefore, there exists
. Therefore, there exists  , and when
, and when  , we have
, we have

Hence

Then

Then, by (5.25), (5.28), we have  . Hence for each
. Hence for each  , and for each
, and for each  , we have
, we have  . Since
. Since  is
is  -pseudomonotone, for each
-pseudomonotone, for each  , and for each
, and for each  , we have
, we have  . Hence
. Hence  . Therefore, the graph of
. Therefore, the graph of  is closed, and
is closed, and  is a closed map. By [16], we know that
is a closed map. By [16], we know that  is upper semicontinuous on
is upper semicontinuous on  . Because
. Because  is
is  -convex in its second variable, for each
-convex in its second variable, for each  ,
,  is convex. It follows from Theorem 3.1 that
is convex. It follows from Theorem 3.1 that

Then, by [17, Theorem 3.1], we know that  is a connected set. The proof of the theorem is completed.
is a connected set. The proof of the theorem is completed.
Let  denote the base of neighborhoods of 0 of
denote the base of neighborhoods of 0 of  . By [18], for each bounded subset
. By [18], for each bounded subset  and for each neighborhood
and for each neighborhood  of 0 in
of 0 in  , we have
, we have

Lemma 5.3.
Let  be a nonempty convex subset of
be a nonempty convex subset of  , and let
, and let  If
If  is lower semicontinuous on
is lower semicontinuous on  , then
, then  is
is  -hemicontinuous on
-hemicontinuous on  .
.
Proof.
For any fixed  , we need to show that the set-valued mapping
, we need to show that the set-valued mapping

is lower semicontinuous at 0. For any  and for any neighborhood
and for any neighborhood  of
of  , there exists
, there exists  such that
such that  and there exists a neighborhood
and there exists a neighborhood  of
of  in
in  , such that
, such that  . Since
. Since  is lower semicontinuous at
is lower semicontinuous at  , for the neighborhood
, for the neighborhood

of  , there exists a neighborhood
, there exists a neighborhood  of
of  such that
such that

For the above  , since
, since  , when
, when  , there exists
, there exists  , and when
, and when  , we have
, we have  By (5.33), we have
By (5.33), we have

Thus there exist  such that
such that  , for all
, for all  . By (5.32), we have
. By (5.32), we have

that is

This means that  is lower semicontinuous at 0. By definition,
is lower semicontinuous at 0. By definition,  is
is  -hemicontinuous on
-hemicontinuous on  .
.
Theorem 5.4.
Let  be a nonempty closed bounded convex subset of
be a nonempty closed bounded convex subset of  , and let
, and let  be a closed convex pointed cone with
be a closed convex pointed cone with  . Assume that for each
. Assume that for each  ,
,  is a
is a  -pseudomonotone, lower semicontinuous mapping. Moreover, assume that the set-valued map
-pseudomonotone, lower semicontinuous mapping. Moreover, assume that the set-valued map  defined by
defined by  is
is  -convex in its second variable, and the set
-convex in its second variable, and the set  is a bounded set in
is a bounded set in  . If there exists a nonempty compact convex subset
. If there exists a nonempty compact convex subset  of
of  , and
, and  , such that
, such that  , for all
, for all  , then
, then  is a nonempty connected compact set.
is a nonempty connected compact set.
Proof.
By Lemma 5.3 and Theorem 5.2,  is a nonempty connected set. Since
is a nonempty connected set. Since  is a compact set, we need only to show that
is a compact set, we need only to show that  is closed. Let
is closed. Let  It is clear that
It is clear that  and
and  . We claim that
. We claim that  Suppose to the contrary that
Suppose to the contrary that  , then there exists
, then there exists  such that
such that

that is

Thus there exists  such that
such that

Hence there exists  such that
such that

where  is the unit ball of
is the unit ball of  . Set
. Set

By definition,  is a neighborhood of zero of
is a neighborhood of zero of  , since
, since  is bounded. Since
is bounded. Since  is lower semicontinuous at
is lower semicontinuous at  , for the above
, for the above  and the above
and the above  , there exists a neighborhood
, there exists a neighborhood  of
of  such that
such that

Since  there exists
there exists  such that when
such that when  , we have
, we have  Thus by (5.42) we have
Thus by (5.42) we have

Thus there exist  for all
for all  . We have
. We have  , and hence
, and hence

Therefore,

Since  and
and  , we have
, we have  . Hence there exists
. Hence there exists  , and when
, and when  we have
we have  . This combining (5.45) implies that
. This combining (5.45) implies that

Hence

By (5.40) and (5.47), we have

On the other hand, since  , we have
, we have

This contradicts (5.48), because  Thus
Thus  . This means that
. This means that  is a closed subset of
is a closed subset of  .
.
References
Lee GM, Kim DS, Lee BS, Yen ND: Vector variational inequality as a tool for studying vector optimization problems. Nonlinear Analysis: Theory, Methods & Applications 1998,34(5):745–765. 10.1016/S0362-546X(97)00578-6
Cheng Y: On the connectedness of the solution set for the weak vector variational inequality. Journal of Mathematical Analysis and Applications 2001,260(1):1–5. 10.1006/jmaa.2000.7389
Gong X-H: Efficiency and Henig efficiency for vector equilibrium problems. Journal of Optimization Theory and Applications 2001,108(1):139–154. 10.1023/A:1026418122905
Gong X-H, Fu WT, Liu W: Super efficiency for a vector equilibrium in locally convex topological vector spaces. In Vector Variational Inequalities and Vector Equilibria, Nonconvex Optimization and Its Applications. Volume 38. Edited by: Giannessi F. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2000:233–252. 10.1007/978-1-4613-0299-5_13
Gong X-H: Connectedness of the solution sets and scalarization for vector equilibrium problems. Journal of Optimization Theory and Applications 2007,133(2):151–161. 10.1007/s10957-007-9196-y
Ansari QH, Oettli W, Schläger D: A generalization of vectorial equilibria. Mathematical Methods of Operations Research 1997,46(2):147–152. 10.1007/BF01217687
Ansari QH, Yao J-C: An existence result for the generalized vector equilibrium problem. Applied Mathematics Letters 1999,12(8):53–56. 10.1016/S0893-9659(99)00121-4
Konnov IV, Yao JC: Existence of solutions for generalized vector equilibrium problems. Journal of Mathematical Analysis and Applications 1999,233(1):328–335. 10.1006/jmaa.1999.6312
Fu J-Y: Generalized vector quasi-equilibrium problems. Mathematical Methods of Operations Research 2000,52(1):57–64. 10.1007/s001860000058
Hou SH, Yu H, Chen GY: On vector quasi-equilibrium problems with set-valued maps. Journal of Optimization Theory and Applications 2003,119(3):485–498.
Tan NX: On the existence of solutions of quasivariational inclusion problems. Journal of Optimization Theory and Applications 2004,123(3):619–638. 10.1007/s10957-004-5726-z
Peng J-W, Lee H-WJ, Yang X-M: On system of generalized vector quasi-equilibrium problems with set-valued maps. Journal of Global Optimization 2006,36(1):139–158. 10.1007/s10898-006-9004-5
Ansari QH, Flores-Bazán F: Recession methods for generalized vector equilibrium problems. Journal of Mathematical Analysis and Applications 2006,321(1):132–146. 10.1016/j.jmaa.2005.07.059
Lin L-J, Ansari QH, Huang Y-J: Some existence results for solutions of generalized vector quasi-equilibrium problems. Mathematical Methods of Operations Research 2007,65(1):85–98. 10.1007/s00186-006-0102-4
Long X-J, Huang N-J, Teo K-L: Existence and stability of solutions for generalized strong vector quasi-equilibrium problem. Mathematical and Computer Modelling 2008,47(3–4):445–451. 10.1016/j.mcm.2007.04.013
Aubin J-P, Ekeland I: Applied Nonlinear Analysis, Pure and Applied Mathematics. John Wiley & Sons, New York, NY, USA; 1984:xi+518.
Warburton AR: Quasiconcave vector maximization: connectedness of the sets of Pareto-optimal and weak Pareto-optimal alternatives. Journal of Optimization Theory and Applications 1983,40(4):537–557. 10.1007/BF00933970
Robertson AP, Robertson W: Topological Vector Spaces, Cambridge Tracts in Mathematics and Mathematical Physics, no. 53. Cambridge University Press, New York, NY, USA; 1964:viii+158.
Acknowledgments
This research was partially supported by the National Natural Science Foundation of China and the Natural Science Foundation of Jiangxi Province, China.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chen, B., Gong, XH. & Yuan, SM. Connectedness and Compactness of Weak Efficient Solutions for Set-Valued Vector Equilibrium Problems. J Inequal Appl 2008, 581849 (2008). https://doi.org/10.1155/2008/581849
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/581849
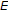
 .
.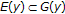
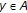 and
and 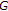 is a KKM map.
is a KKM map.