Skip to main content
Journal of Inequalities and Applications
Download PDF
  • Research Article
  • Open access
  • Published:

Diamond-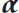 Jensen's Inequality on Time Scales

Journal of Inequalities and Applications volume 2008, Article number: 576876 (2008) Cite this article

Abstract

The theory and applications of dynamic derivatives on time scales have recently received considerable attention. The primary purpose of this paper is to give basic properties of diamond- derivatives which are a linear combination of delta and nabla dynamic derivatives on time scales. We prove a generalized version of Jensen's inequality on time scales via the diamond- integral and present some corollaries, including Hölder's and Minkowski's diamond- integral inequalities.

Publisher note

To access the full article, please see PDF.

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Aveiro, 3810-193, Aveiro, Portugal

    Moulay Rchid Sidi Ammi, Rui A. C. Ferreira & Delfim F. M. Torres

Authors
  1. Moulay Rchid Sidi Ammi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rui A. C. Ferreira
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Delfim F. M. Torres
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Delfim F. M. Torres.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Reprints and permissions

About this article

Cite this article

Sidi Ammi, M.R., Ferreira, R.A.C. & Torres, D.F.M. Diamond-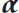 Jensen's Inequality on Time Scales. J Inequal Appl 2008, 576876 (2008). https://doi.org/10.1155/2008/576876

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1155/2008/576876

Keywords