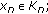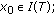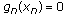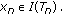- Research Article
- Open access
- Published:
Painleve-Kuratowski Convergences for the Solution Sets of Set-Valued Weak Vector Variational Inequalities
Journal of Inequalities and Applications volume 2008, Article number: 435719 (2008)
Abstract
Painleve-Kuratowski convergence of the solution sets is investigated for the perturbed set-valued weak vector variational inequalities with a sequence of mappings converging continuously. The closedness and Painleve-Kuratowski upper convergence of the solution sets are obtained. We also obtain Painleve-Kuratowski upper convergence when the sequence of mappings converges graphically. By virtue of a sequence of gap functions and a key assumption, Painleve-Kuratowski lower convergence of the solution sets is established. Some examples are given for the illustration of our results.
1. Introduction
Since the concept of vector variational inequality (VVI) was introduced by Giannessi [1] in 1980, many important results on various kinds of vector variational inequality problems have been established, such as existence of solutions, relations with vector optimization, stability of solution set maps, gap function, and duality theories (see, e.g., [2–8] and the references cited therein).
The stability analysis of the solution set maps for the parametric (VVI) problem is of considerable interest amongst researchers in the area. Some results on the semicontinuity of the solution set maps for the parametric (VVI) problem with the parameter perturbed in the space of parameters are now available in the literature. In [4], Khanh and Luu proved the upper semicontinuity of the solution set map for two classes of parametric vector quasivariational inequalities. In [7], Li et al. established the upper semicontinuity property of the solution set map for a perturbed generalized vector quasivariational inequality problem and also obtained the lower semicontinuity property of the solution set map for a perturbed classical scalar variational inequality. In [9], Cheng and Zhu investigated the upper and lower semicontinuities of the solution set map for a parameterized weak vector variational inequality in a finite dimensional Euclidean space by using a scalarization method. In [6], Li and Chen obtained the closedness and upper semicontinuity of the solution set map for a parametric weak vector variational inequality under weaker conditions than those assumed in [9]. Then, under a key assumption, they proved a lower semicontinuity result of the solution set map in a finite dimensional space by using a parametric gap function.
However, there are few investigations on the convergence of the sequence of mappings. In particular, almost no stability results are available for the perturbed (VVI) problem with the sequence of mappings converging continuously or graphically. It appears that the only relevant paper is [10], where Lignola and Morgan considered generalized variational inequality in a reflexive Banach space with a sequence of operators converging continuously and graphically and obtained the convergence of the solution sets under an assumption of pseudomonotonicity. Since the perturbed (VVI) problem with a sequence of mappings converging is different from the parametric (VVI) problem with the parameter perturbed in a space of parameters, these results do not apply to the parametric (VVI) problem with the parameter perturbed in a space of parameters. Thus, it is important to study Painleve-Kuratowski upper and lower convergences of the sequence of solution sets.
In passing, it is worth noting that some stability results are available for the vector optimization and vector equilibrium problems with a sequence of sets converging in the sense of Painleve-Kuratowski (see [11–13]). It is well known that the vector equilibrium problem is a generalization of (VVI) problem. However, if the results obtained for the vector equilibrium problem are to be applied to the (VVI) problem, the required assumptions are on the (VVI) problem as a whole. There is no information about the conditions that are required on the functions defining the (VVI) problem. Clearly, this is unsatisfactory. Our study of the stability properties for the perturbed (VVI) problem with a sequence of converging mappings is under appropriate assumptions on the function defining the (VVI) problem rather than on the (VVI) problem as a whole.
In this paper, we should establish Painleve-Kuratowski upper and lower convergences of the solution sets of the perturbed set-valued weak variational inequity (SWVVI) with a sequence of converging mappings in a Banach space. We first discuss Painleve-Kuratowski upper convergence and closedness of the solution sets. To obtain Painleve-Kuratowski lower convergence of the solution sets, we introduce a sequence of gap functions based on the nonlinear scalarization function introduced by Chen et al. in [14] and a key assumption  imposed on the sequence of gap functions. Then, we obtain Painleve-Kuratowski lower convergence of the solution sets for
imposed on the sequence of gap functions. Then, we obtain Painleve-Kuratowski lower convergence of the solution sets for  .
.
The rest of the paper is organized an follows. In Section 2, we introduce problems (SWVVI) and  , and recall some definitions and important properties of these problems. In Section 3, we investigate Painleve-Kuratowski upper convergence and the closedness of the solution sets. In Section 4, we introduce respective gap functions for problems (SWVVI) and
, and recall some definitions and important properties of these problems. In Section 3, we investigate Painleve-Kuratowski upper convergence and the closedness of the solution sets. In Section 4, we introduce respective gap functions for problems (SWVVI) and  and then establish Painleve-Kuratowski lower convergence of the solution sets under a key assumption.
and then establish Painleve-Kuratowski lower convergence of the solution sets under a key assumption.
2. Preliminaries
Let  and
and  be two Banach spaces and let
be two Banach spaces and let  be the set of all linear continuous mappings from
be the set of all linear continuous mappings from  to
to  . The value of a linear mapping
. The value of a linear mapping  at
at  is denoted by
is denoted by  . Let
. Let  be a closed and convex cone with nonempty interior, that is,
be a closed and convex cone with nonempty interior, that is,  . We define the ordering relations as follows.
. We define the ordering relations as follows.
For any  ,
,

Consider the set-valued weak vector variational inequality (SWVVI) problem for finding  and
and  such that
such that

where  is a nonempty subset and
is a nonempty subset and  is a set-valued mapping.
is a set-valued mapping.
For a sequence of set-valued mappings  , we define a sequence of set-valued weak vector variational inequality
, we define a sequence of set-valued weak vector variational inequality  problems for finding
problems for finding  and
and  such that
such that

where  is a sequence of nonempty subsets.
is a sequence of nonempty subsets.
We denote the solution sets of problems (SWVVI) and  by
by  and
and  , respectively, that is,
, respectively, that is,

Throughout this paper, we assume that  and
and  . The stability analysis is to investigate the behaviors of the solution sets
. The stability analysis is to investigate the behaviors of the solution sets  and
and  .
.
Now we recall some basic definitions and properties of problems (SWVVI) and  . For each
. For each  and a subset
and a subset  , let the open
, let the open  -neighborhood of
-neighborhood of  be defined as
be defined as  . The notation
. The notation  denotes the open ball with center
denotes the open ball with center  and radius
and radius  .
.
In the following, we introduce some concepts of the convergence of set sequences and mapping sequences which will be used in the sequel. Define

where  denotes the set of all positive integer numbers and
denotes the set of all positive integer numbers and  is an integer in
is an integer in  .
.
Definition 2.1 (see [11, 15]).
Let  be a normed space. A sequence of sets
be a normed space. A sequence of sets  is said to converge in the sense of Painleve-Kuratowski (P.K.) to
is said to converge in the sense of Painleve-Kuratowski (P.K.) to  (i.e.,
(i.e.,  ) if
) if

with

It is said that the sequence  upper converges in the sense of Painleve-Kuratowski to
upper converges in the sense of Painleve-Kuratowski to  if
if  . Similarly, the sequence
. Similarly, the sequence  is said to lower converge in the sense of Painleve-Kuratowski to
is said to lower converge in the sense of Painleve-Kuratowski to  if
if  .
.
Definition 2.2 (see [15]).
A set-valued mapping  is outer semicontinuous (osc) at
is outer semicontinuous (osc) at  if
if  with
with  .
.
On the other hand, it is inner semicontinuous (isc) at  if
if  with
with  .
.
The set-valued mapping is said to be continuous at  , written as
, written as  as
as  if it is both outer semicontinuous and inner semicontinuous.
if it is both outer semicontinuous and inner semicontinuous.
Definition 2.3 (see [15]).
Let  be a sequence of set-valued mappings and
be a sequence of set-valued mappings and  be a set-valued mapping. It is said that the sequence
be a set-valued mapping. It is said that the sequence  converges continuously to
converges continuously to  at
at  if
if

If  converges continuously to
converges continuously to  at every
at every  , then it is said that
, then it is said that  converges continuously to
converges continuously to  on
on  .
.
Let  be a set-valued map, the graph of
be a set-valued map, the graph of  is defined as
is defined as

Applying set convergence theory to the graphs of the mappings, we obtain the graphical convergence of the sequence of mappings.
Definition 2.4 (see [15]).
For a sequence of mappings  , the graphical outer limit, denoted by
, the graphical outer limit, denoted by  , is the mapping which has as its graph the set
, is the mapping which has as its graph the set  :
:

The graphical inner limit, denote by  , is the mapping having as its graph the set
, is the mapping having as its graph the set  :
:

If the outer and inner limits of the mappings  agree, it is said that their graphical limit,
agree, it is said that their graphical limit,  , exists. In this case, the notation
, exists. In this case, the notation  is used, and the sequence
is used, and the sequence  of mappings is said to converge graphically to
of mappings is said to converge graphically to  . Clearly,
. Clearly,  .
.
Proposition 2.5 (see [15]).
For any sequence of mappings  , it holds that
, it holds that

where the unions are taken over all sequences  . Thus, the sequence
. Thus, the sequence  converges graphically to
converges graphically to  if and only if, at each point
if and only if, at each point  , it holds that
, it holds that

From Proposition 2.5 and Definition 2.3, the following proposition follows readily.
Proposition 2.6.
Let  be a sequence of set-valued mappings and
be a sequence of set-valued mappings and  be a set-valued mapping. Then, the sequence
be a set-valued mapping. Then, the sequence  outer converges graphically to
outer converges graphically to  if and only if
if and only if  outer converges continuously to
outer converges continuously to  , that is,
, that is,

Definition 2.7 (see [10]).
Given a sequence of mappings  ,
,  is said to be uniformly bounded if for any sequence
is said to be uniformly bounded if for any sequence  contained in a bounded set, there exists a positive number
contained in a bounded set, there exists a positive number  such that for any sequence
such that for any sequence  with
with  for all
for all  , it holds that
, it holds that

Proposition 2.8 (see [16]).
For any fixed  ,
,  ,
,  , and the nonlinear scalarization function
, and the nonlinear scalarization function  defined by
defined by  :
:
(i) is a continuous and convex function on
is a continuous and convex function on  ;
;
(ii)
(iii)
3. Painleve-Kuratowski Upper Convergence of the Solution Sets
In this section, our focus is on the Painleve-Kuratowski upper convergence and the closedness of the solution sets.
Theorem 3.1.
Suppose that
(i) outer converges continuously to
outer converges continuously to  , that is,
, that is,

(ii) ;
;
(iii) are uniformly bounded.
are uniformly bounded.
Then,  , that is to say for any subsequence
, that is to say for any subsequence  of solutions to
of solutions to  , if
, if  , then
, then  is a solution to
is a solution to  .
.
Proof.
The proof is listed on contradiction arguments. On a contrary, suppose that  but
but  .
.
From  , we have
, we have  , where
, where  and
and  is a subsequence of
is a subsequence of  . Then, there exists
. Then, there exists  such that
such that

Since  , it is clear that for any
, it is clear that for any  , there exists a sequence
, there exists a sequence  with
with  and
and  , as
, as  . Thus,
. Thus,

Since  and
and  , we have
, we have  . Now, we note that
. Now, we note that  . Thus, for all
. Thus, for all  , there exists
, there exists  such that
such that

From the uniform boundedness of  , we may assume, without loss of generality, that
, we may assume, without loss of generality, that  (though a subsequence of
(though a subsequence of  if necessary). By (i), we get
if necessary). By (i), we get  . Thus,
. Thus,

It follows from (3.3) and the closedness of  that
that

which is a contradiction to (3.4). This completed the proof.
Remark 3.2.
Let  and
and  , where
, where  is a reflexive Banach space and
is a reflexive Banach space and  is its dual. If we take
is its dual. If we take  ,
,  reduce to the generalized variational inequality problems with perturbed operators
reduce to the generalized variational inequality problems with perturbed operators  considered in [10, Section 3]. The convergence for the solution sets of
considered in [10, Section 3]. The convergence for the solution sets of  was studied under the the pseudomonotonicity assumption in [10]. Furthermore, if
was studied under the the pseudomonotonicity assumption in [10]. Furthermore, if  and
and  are vector-valued mappings, then
are vector-valued mappings, then  reduce to
reduce to  considered in [10, Section 2]. We also notice that the Painleve-Kuratowski upper convergence of the solution sets of
considered in [10, Section 2]. We also notice that the Painleve-Kuratowski upper convergence of the solution sets of  is obtained under weaker assumptions than these assumed in [10, Proposition 2.1] for obtaining convergence of the solution sets.
is obtained under weaker assumptions than these assumed in [10, Proposition 2.1] for obtaining convergence of the solution sets.
From Proposition 2.5 and Theorem 3.1, we obtain readily the following corollary.
Corollary 3.3.
Suppose that
(i) outer converges graphically to
outer converges graphically to  , written as
, written as  that is,
that is,

(ii) ;
;
(iii) is uniformly bounded.
is uniformly bounded.
Then,  .
.
Remark 3.4.
Let  . Then, problems
. Then, problems  reduce to the generalized variational inequalities with perturbed operators considered in [10, Proposition 3.1] and the convergence was obtained under the assumption that the operators converge graphically.
reduce to the generalized variational inequalities with perturbed operators considered in [10, Proposition 3.1] and the convergence was obtained under the assumption that the operators converge graphically.
Theorem 3.5.
Suppose that
(i) is osc on
is osc on  , that is, for all
, that is, for all  ,
,  ;
;
(ii) and
and  are compact sets.
are compact sets.
Then,  is a compact set.
is a compact set.
Proof.
First, we prove that  is a closed set. Take any sequence
is a closed set. Take any sequence  with
with  . Then, there exists
. Then, there exists  such that
such that

It follows from the compactness of  that
that  . Suppose that
. Suppose that  , we have
, we have

Since  is a compact set, without loss of generality, we assume that there exists a
is a compact set, without loss of generality, we assume that there exists a  such that
such that  . Thus, we have
. Thus, we have  . By (i), we get a
. By (i), we get a  . It follows from (3.8) and the closedness of
. It follows from (3.8) and the closedness of  that
that

which contradicts with (3.9). Hence,  and
and  is a closed set. Next, it follows from
is a closed set. Next, it follows from  and the compactness of
and the compactness of  that
that  is a compact set. The proof is completed.
is a compact set. The proof is completed.
Similarly, we have the following result.
Theorem 3.6.
For any  , suppose that
, suppose that
(i) is osc on
is osc on  , that is,
, that is, 

(ii) and
and  are compact sets.
are compact sets.
Then,  is a compact set.
is a compact set.
4. Painleve-Kuratowski Lower Convergence of the Solution Sets
In this section, we focus on the lower convergence of the solution sets. Assume that  and
and  are compact sets and that for each
are compact sets and that for each  ,
,  and
and  are compact sets. Let
are compact sets. Let  and
and  be functions defined by
be functions defined by

Since  ,
,  ,
,  , and
, and  are compact sets and
are compact sets and  is continuous,
is continuous,  and
and  are well defined.
are well defined.
Proposition 4.1.
-
(i)
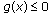
for all
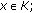 ;
; -
(ii)

for all
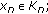
-
(iii)

if and only if
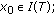
-
(iv)
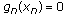
if and only if
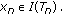
Proof.
Define

We first prove that  . On a contrary, we suppose that this is false. Then, there exist
. On a contrary, we suppose that this is false. Then, there exist  and
and  such that
such that  . Thus,
. Thus,

which is impossible when  . Therefore,
. Therefore,

By the same taken, we can show that

On the other hand, if  , then there exists a
, then there exists a  such that
such that  , that is,
, that is,

From Proposition 2.8, (4.6) is valid if and only if for any  ,
,

Clearly, (4.7) holds if and only if for any  ,
,  , that is,
, that is,  . This proves that (iii) holds.
. This proves that (iii) holds.
Similarly, we can show that (iv) holds.
The functions  are called the gap functions for
are called the gap functions for  if properties (ii) and (iv) of Proposition 4.1 are satisfied.
if properties (ii) and (iv) of Proposition 4.1 are satisfied.
In view of hypothesis  of [6, 17, 18], we introduce the following key assumption:
of [6, 17, 18], we introduce the following key assumption:
(H
g
):given the sequence  for any
for any  , there exist an
, there exist an  and an
and an  such that
such that  for all
for all  and for all
and for all  .
.
Geometrically, the hypothesis  means that given a sequence of mappings
means that given a sequence of mappings  , we can find for any small positive number
, we can find for any small positive number  , a small positive number
, a small positive number  and a large-enough positive number
and a large-enough positive number  such that for all
such that for all  , if a feasible point
, if a feasible point  is away from the solution sets
is away from the solution sets  by distance of at least
by distance of at least  , then the values of all gap functions for
, then the values of all gap functions for  is less than or equal to at least some "
is less than or equal to at least some " ."
."
To illustrate assumption  , we give the following example.
, we give the following example.
Example 4.2.
Let

Consider problems  . From direct computation, we obtain
. From direct computation, we obtain  . To check assumption
. To check assumption  , we take
, we take  . Then,
. Then,

For any given  , we take
, we take  and
and  . Then, for all
. Then, for all  and for all
and for all  , we have
, we have  . Hence, assumption
. Hence, assumption  is valid.
is valid.
Lemma 4.3.
Suppose that
(i) inner converges continuously to
inner converges continuously to  , that is,
, that is,

(ii) ;
;
(iii) is a compact set.
is a compact set.
Then, for any  ,
,  and sequence
and sequence  with
with  and
and  , there exists a subsequence
, there exists a subsequence  of
of  and
and  such that
such that  for all
for all  .
.
Proof.
Let  be a function defined by
be a function defined by

From the continuity of  with respect to
with respect to  , the compactness of
, the compactness of  and [19, Chapter 3, Section 1, Proposition 23], we have that
and [19, Chapter 3, Section 1, Proposition 23], we have that  is continuous with respect to
is continuous with respect to  . Thus, from the compactness of
. Thus, from the compactness of  , there exists a
, there exists a  such that
such that

From assumption (i), there exists a sequence  satisfying
satisfying  such that
such that

It follows from the compactness of  that there exists
that there exists  with
with  such that
such that

Since  is compact, we assume, without loss of generality, that
is compact, we assume, without loss of generality, that  . Thus, it follows from (ii) that
. Thus, it follows from (ii) that  Consequently,
Consequently,

So, for any  , there exists an
, there exists an  such that
such that  for all
for all  . By (4.14), we have
. By (4.14), we have

Hence, the result holds.
Set  and
and  . We have the following lemma.
. We have the following lemma.
Lemma 4.4.
Suppose that for 
 is osc on
is osc on  , that is, for
, that is, for 

Then,  if and only if for all
if and only if for all  ,
,  such that
such that  for all
for all  .
.
Proof.
We assume  , but there exists an
, but there exists an  such that for all
such that for all  there exists an
there exists an  satisfying
satisfying  . Then, there exists a sequence
. Then, there exists a sequence  with
with  , but
, but  . From Theorem 3.5, we note that
. From Theorem 3.5, we note that  is a compact set. Without loss of generality, we assume
is a compact set. Without loss of generality, we assume  and
and  . Thus, for any sequence
. Thus, for any sequence  satisfying
satisfying  with
with  , we have
, we have  . Letting
. Letting  , we get
, we get  . Therefore, there does not exist any sequence
. Therefore, there does not exist any sequence  satisfying
satisfying  . This is a contradiction to
. This is a contradiction to  .
.
Conversely, suppose that for any  such that
such that  for all
for all  . From Theorem 3.6, we note that
. From Theorem 3.6, we note that  is compact for all
is compact for all  . Thus, for any
. Thus, for any  , there exists
, there exists  such that
such that  for all
for all  . So, we have
. So, we have  and
and  . Therefore, the result of the lemma follows readily.
. Therefore, the result of the lemma follows readily.
Now, we are in a position to state and prove our main result in the following theorem.
Theorem 4.5.
Suppose that assumption  holds and that the following conditions are satisfied:
holds and that the following conditions are satisfied:
(i) is osc on
is osc on  for
for  that is, for
that is, for 

(ii) inner converge continuously to
inner converge continuously to  , that is,
, that is,

(iii) is a compact set;
is a compact set;
(iv) .
.
Then,  .
.
Proof.
We prove the result via contradiction. On a contrary, we assume, by Lemma 4.4, that there exists an  such that for any
such that for any  , we have
, we have  satisfying
satisfying

that is, there exists a sequence  satisfying
satisfying

From the compactness of  , we can assume, without loss of generality, that
, we can assume, without loss of generality, that  . Then, there exists an
. Then, there exists an  such that
such that  . It is clear that
. It is clear that  for any positive integer
for any positive integer  . Since
. Since  , there exist a sequence
, there exist a sequence  satisfying
satisfying  . Then, there exists an
. Then, there exists an  such that
such that  for all
for all  .
.
Now, we note that  . Otherwise, there would exist a sequence
. Otherwise, there would exist a sequence  with
with  such that
such that  . Thus, for
. Thus, for  , we have
, we have

This implies that  , which contradicts with (4.21). Thus,
, which contradicts with (4.21). Thus,

By hypothesis  , there exist, for any
, there exist, for any  , an
, an  and an
and an  such that for all
such that for all  and for all
and for all  ,
,  . In particular, it follows from (4.23) that
. In particular, it follows from (4.23) that

By virtue of Lemma 4.3, there exists, for any  , a subsequence
, a subsequence  of
of  and
and  such that
such that

We can take  such that
such that  . Thus,
. Thus,

that is,

So, for any  ,
,  . Thus, there exists a
. Thus, there exists a  such that
such that

Consequently, by Proposition 2.8, we have  , which shows that
, which shows that  . This contradicts with
. This contradicts with  . Therefore, our result follows readily.
. Therefore, our result follows readily.
Now, we explain the applicability of Theorem 4.5 through an example.
Example 4.6.
Consider Example 4.2. It follows from a direct computation that  . It is easy to testify that assumption
. It is easy to testify that assumption  holds and so are conditions (i)–(v) of Theorem 4.5. Obviously, the solution sets of problem
holds and so are conditions (i)–(v) of Theorem 4.5. Obviously, the solution sets of problem  lower converge in the sense of Painleve-Kuratowski.
lower converge in the sense of Painleve-Kuratowski.
References
Giannessi F: Theorems of alternative, quadratic programs and complementarity problems. In Variational Inequalities and Complementarity Problems (Proc. Internat. School, Erice, 1978). Edited by: Cottle RW, Giannessi F, Lions J-L. John Wiley & Sons, Chichester, UK; 1980:151–186.
Chen GY: Existence of solutions for a vector variational inequality: an extension of the Hartmann-Stampacchia theorem. Journal of Optimization Theory and Applications 1992,74(3):445–456. 10.1007/BF00940320
Chen GY, Li SJ: Existence of solutions for a generalized vector quasivariational inequality. Journal of Optimization Theory and Applications 1996,90(2):321–334. 10.1007/BF02190001
Khanh PQ, Luu LM: Upper semicontinuity of the solution set to parametric vector quasivariational inequalities. Journal of Global Optimization 2005,32(4):569–580. 10.1007/s10898-004-2694-7
Lee JR, Park C, Shin DY: On the stability of generalized additive functional inequalities in Banach spaces. Journal of Inequalities and Applications 2008, 2008:-13.
Li SJ, Chen CR: Stability of weak vector variational inequality. Nonlinear Analysis: Theory, Methods & Applications 2009,70(4):1528–1535. 10.1016/j.na.2008.02.032
Li SJ, Chen GY, Teo KL: On the stability of generalized vector quasivariational inequality problems. Journal of Optimization Theory and Applications 2002,113(2):283–295. 10.1023/A:1014830925232
Yang XQ: Vector variational inequality and its duality. Nonlinear Analysis: Theory, Methods & Applications 1993,21(11):869–877. 10.1016/0362-546X(93)90052-T
Cheng YH, Zhu DL: Global stability results for the weak vector variational inequality. Journal of Global Optimization 2005,32(4):543–550. 10.1007/s10898-004-2692-9
Lignola MB, Morgan J: Generalized variational inequalities with pseudomonotone operators under perturbations. Journal of Optimization Theory and Applications 1999,101(1):213–220. 10.1023/A:1021783313936
Durea M: On the existence and stability of approximate solutions of perturbed vector equilibrium problems. Journal of Mathematical Analysis and Applications 2007,333(2):1165–1179. 10.1016/j.jmaa.2006.12.009
Lucchetti RE, Miglierina E: Stability for convex vector optimization problems. Optimization 2004,53(5–6):517–528. 10.1080/02331930412331327166
Miglierina E, Molho E: Scalarization and stability in vector optimization. Journal of Optimization Theory and Applications 2002,114(3):657–670. 10.1023/A:1016031214488
Chen GY, Yang XQ, Yu H: A nonlinear scalarization function and generalized quasi-vector equilibrium problems. Journal of Global Optimization 2005,32(4):451–466. 10.1007/s10898-003-2683-2
Rockafellar RT, Wets RJ-B: Variational Analysis, Fundamental Principles of Mathematical Sciences. Volume 317. Springer, Berlin, Germany; 1998:xiv+733.
Chen GY, Huang X, Yang X: Vector Optimization: Set-Valued and Variational Analysis, Lecture Notes in Economics and Mathematical Systems. Volume 541. Springer, Berlin, Germany; 2005:x+306.
Zhao J: The lower semicontinuity of optimal solution sets. Journal of Mathematical Analysis and Applications 1997,207(1):240–254. 10.1006/jmaa.1997.5288
Kien BT: On the lower semicontinuity of optimal solution sets. Optimization 2005,54(2):123–130. 10.1080/02331930412331330379
Aubin J-P, Ekeland I: Applied Nonlinear Analysis, Pure and Applied Mathematics. John Wiley & Sons, New York, NY, USA; 1984:xi+518.
Acknowledgment
This research was partially supported by the National Natural Science Foundation of China (Grants no. 10871216 and no. 60574073).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Fang, Z.M., Li, S.J. & Teo, K.L. Painleve-Kuratowski Convergences for the Solution Sets of Set-Valued Weak Vector Variational Inequalities. J Inequal Appl 2008, 435719 (2008). https://doi.org/10.1155/2008/435719
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/435719
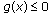
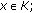 ;
;