- Research Article
- Open access
- Published:
A Note on Convergence Analysis of an SQP-Type Method for Nonlinear Semidefinite Programming
Journal of Inequalities and Applications volume 2008, Article number: 218345 (2007)
Abstract
We reinvestigate the convergence properties of the SQP-type method for solving nonlinear semidefinite programming problems studied by Correa and Ramirez (2004). We prove, under the strong second-order sufficient condition with the sigma term, that the local SQP-type method is quadratically convergent and the line search SQP-type method is globally convergent.
1. Introduction
We consider the following nonlinear semidefinite programming:

where  ,
,  ,
,  , and
, and  are twice continuously differentiable functions,
are twice continuously differentiable functions,  is the linear space of all
is the linear space of all  real symmetric matrices, and
real symmetric matrices, and  is the cone of all
is the cone of all  symmetric positive semidefinite matrices.
symmetric positive semidefinite matrices.
Fares et al. (2002) [1] studied robust control problems via sequential semidefinite programming technique. They obtained the local quadratic convergence rate of the proposed SQP-type method and employed a partial augmented Lagrangian method to deal with the problems addressed there. Correa and Ramirez (2004) [2] systematically studied an SQP-type method for solving nonlinear SDP problems and analyzed the convergence properties, they obtained the global convergence and local quadratic convergence rate. Both papers used the same subproblems to generate search directions, but employed different merit functions for line search. The convergence analysis of both papers depends on a set of second-order conditions without sigma term, which is stronger than no gap second-order optimality condition with sigma term.
Comparing with the work by Correa and Ramirez (2004) [2], in this note, we make some modifications to the convergence analysis, and prove that all results in [2] still hold under the strong second-order sufficient condition with the sigma term.
It should be pointed out that the importance of exploring numerical methods for solving nonlinear semidefinite programming problems has been recognized in the optimization community. For instance, Kočvara and Stingl [3, 4] have developed PENNLP and PENBMI codes for nonlinear semidefinite programming and semidefinite programming with bilinear matrix inequality constraints, respectively. Recently, Sun et al. (2007) [5] considered the rate of convergence of the classical augmented Lagrangian method and Noll (2007) [6] investigated the convergence properties of a class of nonlinear Lagrangian methods.
In Section 2, we introduce preliminaries including differential properties of the metric projector onto  and optimality conditions for problem (1.1). In Section 3, we prove, under the strong second-order sufficient condition with the sigma term, that the local SQP-type method has the quadratic convergence rate and the global algorithm with line search is convergence.
and optimality conditions for problem (1.1). In Section 3, we prove, under the strong second-order sufficient condition with the sigma term, that the local SQP-type method has the quadratic convergence rate and the global algorithm with line search is convergence.
2. Preliminaries
We use  to denote the set of all the matrices of
to denote the set of all the matrices of  rows and
rows and  columns. For
columns. For  and
and  in
in  , we use the Frobenius inner product
, we use the Frobenius inner product  , and the Frobenius norm
, and the Frobenius norm  , where "tr" denotes the trace operation of a square matrix.
, where "tr" denotes the trace operation of a square matrix.
For a given matrix  , its spectral decomposition is
, its spectral decomposition is

where  is the diagonal matrix of eigenvalues of
is the diagonal matrix of eigenvalues of  and
and  is a corresponding orthogonal matrix. We can express
is a corresponding orthogonal matrix. We can express  and
and  as
as

where  ,
,  ,
,  are the index sets of positive, zero, negative eigenvalues of
are the index sets of positive, zero, negative eigenvalues of  , respectively.
, respectively.
2.1. Semismoothness of the Metric Projector
In this subsection, let  ,
,  , and
, and  be three arbitrary finite-dimensional real spaces with a scalar product
be three arbitrary finite-dimensional real spaces with a scalar product  and its norm
and its norm  . We introduce some properties of the metric projector, especially its strong semismoothness.
. We introduce some properties of the metric projector, especially its strong semismoothness.
The next lemma is about the generalized Jacobian for composite functions, proposed in [7].
Lemma 2.1.
Let  be a continuously differentiable function on an open neighborhood
be a continuously differentiable function on an open neighborhood  of
of  and let
and let  be a locally Lipschitz continuous function on the open set
be a locally Lipschitz continuous function on the open set  containing
containing  . Suppose that
. Suppose that  is directionally differentiable at every point in
is directionally differentiable at every point in  and that
and that  is onto. Then it holds that
is onto. Then it holds that

where  is defined by
is defined by  ,
,  .
.
The following concept of semismoothness was first introduced by Mifflin [8] for functionals and was extended by Qi and Sun in [9] to vector valued functions.
Definition 2.2.
Let  be a locally Lipschitz continuous function on the open set
be a locally Lipschitz continuous function on the open set  . One says that
. One says that  is semismooth at a point
is semismooth at a point  if
if
(i) is directionally differentiable at
is directionally differentiable at  ;
;
(ii)for any  and
and  with
with  ,
,

Furthermore,  is said to be strongly semismooth at
is said to be strongly semismooth at  if
if  is semismooth at
is semismooth at  and for any
and for any  and
and  with
with  ,
,

Let  be a closed convex set in a Banach space
be a closed convex set in a Banach space  , and let
, and let  be the metric projector over
be the metric projector over  . It is well known in [10, 11] that
. It is well known in [10, 11] that  is
is  -differentiable almost everywhere in
-differentiable almost everywhere in  and for any
and for any  ,
,  is well defined.
is well defined.
Suppose  , then it has the spectral decomposition as (2.1), then the merit projector of
, then it has the spectral decomposition as (2.1), then the merit projector of  to
to  is denoted by
is denoted by  and
and

where  .
.
For our discussion, we know from [12] that the projection operator  is directionally differentiable everywhere in
is directionally differentiable everywhere in  and is a strongly semismooth matrix-valued function. In fact, for any
and is a strongly semismooth matrix-valued function. In fact, for any  ,
,  , there exists
, there exists  , satisfying
, satisfying

2.2. Optimality Conditions
Let the Lagrangian function of (1.1) be

Robinson's constraint qualification(CQ) is said to hold at a feasible point  if
if

If  is a locally optimal solution to (1.1) and Robinson's CQ holds at
is a locally optimal solution to (1.1) and Robinson's CQ holds at  , then there exist Lagrangian multipliers
, then there exist Lagrangian multipliers  , such that the following KKT condition holds:
, such that the following KKT condition holds:

which is equivalent to  , where
, where

Let  be the set of all the Lagrangian multipliers satisfying (2.10). Then
be the set of all the Lagrangian multipliers satisfying (2.10). Then  is a nonempty, compact convex set of
is a nonempty, compact convex set of  if and only if Robinson's CQ holds at
if and only if Robinson's CQ holds at  , see [13]. Moreover, it follows from [13] that the constraint nondegeneracy condition is a sufficient condition for Robinson constraint qualification. In the setting of the problem (1.1), the constraint nondegeneracy condition holding at a feasible point
, see [13]. Moreover, it follows from [13] that the constraint nondegeneracy condition is a sufficient condition for Robinson constraint qualification. In the setting of the problem (1.1), the constraint nondegeneracy condition holding at a feasible point  can be expressed as
can be expressed as

where  is the lineality space of the tangent cone of
is the lineality space of the tangent cone of  at
at  . If
. If  , a locally optimal solution to (1.1), is nondegenerate, then
, a locally optimal solution to (1.1), is nondegenerate, then  is a singleton.
is a singleton.
For a KKT point  of (1.1), without loss of generality, we assume that
of (1.1), without loss of generality, we assume that  and
and  have the spectral decomposition forms
have the spectral decomposition forms

We state the strong second-order sufficient condition (SSOSC) coming from [7].
Definition 2.3.
Let  be a stationary point of (1.1) such that (2.12) holds at
be a stationary point of (1.1) such that (2.12) holds at  . One says that the strong second-order sufficient condition holds at
. One says that the strong second-order sufficient condition holds at  if
if

where  ,
,  is the affine hull of the critical cone
is the affine hull of the critical cone  :
:

And the linear-quadratic function  is defined by
is defined by


is the Moore-Penrose pseudoinverse of  .
.
The next proposition relates the SSOSC and nondegeneracy condition to nonsingularity of Clarke's Jacobian of the mapping  defined by (2.11). The details of this proof can be found in [7].
defined by (2.11). The details of this proof can be found in [7].
Proposition 2.4.
Let  be a KKT point of (1.1). If nondegeneracy condition (2.12) and SSOSC (2.14) hold at
be a KKT point of (1.1). If nondegeneracy condition (2.12) and SSOSC (2.14) hold at  , then any element in
, then any element in  is nonsingular, where
is nonsingular, where  is defined by (2.11).
is defined by (2.11).
3. Convergence Analysis of the SQP-Type Method
In this section, we analyze the local quadratic convergence rate of an SQP-type method and then prove that the SQP-type method proposed in [2] is globally convergent. The analysis is based on the strong second-order sufficient condition, which is weaker than the conditions used in [1, 2].
3.1. Local Convergence Rate
Linearizing (1.1) at the current point  , we obtain the following tangent quadratic problem:
, we obtain the following tangent quadratic problem:

where  . Let
. Let  be a KKT point of (3.1), then we have
be a KKT point of (3.1), then we have  , where
, where

The following algorithm is an SQP-type algorithm for solving (1.1), which is based on computing at each iteration a primal-dual stationary point  of (3.1).
of (3.1).
Algorithm 3.1.
Step 1.
Given an initial iterate point  . Compute
. Compute  ,
,  ,
,  ,
,  and
and  . Set
. Set  .
.
Step 2.
If  ,
,  ,
,  , stop.
, stop.
Step 3.
Compute  , and find a solution
, and find a solution  to (3.1).
to (3.1).
Step 4.
Set  .
.
Step 5.
Compute  ,
,  ,
,  ,
,  and
and  . Set
. Set  and go to step 2.
and go to step 2.
From item (f) of [7, Theorem 4.1], we obtain the error between  and
and  directly.
directly.
Theorem 3.2.
Suppose that  are twice continuously differentiable and their derivatives are locally Lipschitz in a neighborhood of a local solution
are twice continuously differentiable and their derivatives are locally Lipschitz in a neighborhood of a local solution  to (1.1). Suppose nondegeneracy condition (2.12) and SSOSC (2.14) hold at
to (1.1). Suppose nondegeneracy condition (2.12) and SSOSC (2.14) hold at  . Then there exists a neighborhood
. Then there exists a neighborhood  of
of  such that if
such that if  in
in  , (3.1) has a local solution
, (3.1) has a local solution  together with corresponding Lagrangian multiplies
together with corresponding Lagrangian multiplies  satisfying
satisfying

Now we are in a position to state that the sequence of primal-dual points generated by Algorithm 3.1 has quadratic convergence rate.
Theorem 3.3.
Suppose that  are twice continuously differentiable and their derivatives are locally Lipschitz in a neighborhood of a local solution
are twice continuously differentiable and their derivatives are locally Lipschitz in a neighborhood of a local solution  to (1.1). Suppose nondegeneracy condition (2.12) and SSOSC (2.14) hold at
to (1.1). Suppose nondegeneracy condition (2.12) and SSOSC (2.14) hold at  . Consider Algorithm 3.1, in which
. Consider Algorithm 3.1, in which  is a minimum norm stationary point of the tangential quadratic problem (3.1). Then there exists a neighborhood
is a minimum norm stationary point of the tangential quadratic problem (3.1). Then there exists a neighborhood  of
of  such that, if
such that, if  , Algorithm 3.1 is well defined and the sequence
, Algorithm 3.1 is well defined and the sequence  converges quadratically to
converges quadratically to  .
.
Proof.
By Theorem 3.2, we know Algorithm 3.1 is well defined. Let

then

where  is the minimum norm solution to (3.1), and
is the minimum norm solution to (3.1), and  ,
,  are the associated multipliers. Using Taylor expansion of (3.2) at
are the associated multipliers. Using Taylor expansion of (3.2) at  , noting that
, noting that  ,
,  , and (3.5), we obtain
, and (3.5), we obtain

As the projection operator  is strongly semismooth, we have that there exists
is strongly semismooth, we have that there exists  such that
such that

Since

we have

Noting the fact that  , by Taylor expansion of the third equation of (3.2) at
, by Taylor expansion of the third equation of (3.2) at  , we obtain
, we obtain

Therefore, we can conclude that

Since the nondegeneracy condition (2.12) and SSOSC (2.14) hold, we have from Proposition 2.4 that (3.11) implies the quadratic convergence of the sequence  .
.
3.2. The Global Convergence
The tangential quadratic problem constrained here is slightly more general than (3.1) in the sense that the Hessian of the Lagrangian  is replaced by some positive definite matrix
is replaced by some positive definite matrix  . Thus the tangential quadratic problem in
. Thus the tangential quadratic problem in  now becomes
now becomes

The KKT systemof (3.12) is

To obtain theglobal convergence, we use the Han penalty function given by [14], as a merit function and Armijo line search. For problem (1.1), the Han penalty function is defined by

where  is the smallest eigenvalue of
is the smallest eigenvalue of  ,
,  denote
denote  and
and  is a positive constant. The following proposition comes from [2] directly.
is a positive constant. The following proposition comes from [2] directly.
Proposition 3.4.
-
(i)
If
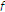 ,
, 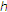 ,
, 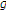 have a directional derivative at
have a directional derivative at  in the direction
in the direction 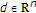 , then
, then  has also a directional derivative at
has also a directional derivative at  in the direction
in the direction 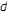 . If, in addition,
. If, in addition,  is feasible for (1.1), we have
is feasible for (1.1), we have 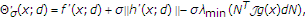 (3.15)
(3.15)
where  is the matrix whose columns
is the matrix whose columns  form an orthonormal basis of
form an orthonormal basis of  .
.
(ii)If  is a feasible point of (1.1) and
is a feasible point of (1.1) and  has a local minimum at
has a local minimum at  , then
, then  is the local solution to (1.1). Furthermore, if
is the local solution to (1.1). Furthermore, if  ,
,  ,
,  are differentiable at
are differentiable at  and nondegeneracy condition (2.12) holds at
and nondegeneracy condition (2.12) holds at  , then
, then  .
.
(iii)If  and
and  , then
, then  .
.
To discuss the conditions ensuring the exactness of  , we need the following lemma from (3.10).
, we need the following lemma from (3.10).
Lemma 3.5.
Suppose nondegeneracy condition (2.12) and SSOSC (2.14) hold at  . Then there exists
. Then there exists  , such that for any
, such that for any  there exist a neighborhood
there exist a neighborhood  of
of  and a neighborhood
and a neighborhood  of
of  , for any
, for any  , the problem
, the problem

has a unique solution denote  . The function
. The function  is locally Lipschitz continuous and semismooth on
is locally Lipschitz continuous and semismooth on  . Furthermore, there exists
. Furthermore, there exists  , for any
, for any  ,
,

where

is the augmented Lagrangian function with the penalty parameter  for (1.1).
for (1.1).
Theorem 3.6.
Suppose that  ,
,  ,
,  are twice differentiable around a local solution
are twice differentiable around a local solution  to (1.1), at which nondegeneracy condition (2.12) and SSOSC (2.14) hold. If
to (1.1), at which nondegeneracy condition (2.12) and SSOSC (2.14) hold. If  , then
, then  has a strict local minimum at
has a strict local minimum at  .
.
Proof.
For the definition of the projection operator  , we have
, we have

and for any  ,
,  ,
,

Then

holds for any  . So taking
. So taking  and
and  , we obtain that
, we obtain that

which implies

Since  , for any fixed
, for any fixed  , there exists a neighborhood
, there exists a neighborhood  of
of  such that
such that

From Lemma 3.5, we know that there exist an  and a neighborhood
and a neighborhood  of
of  where
where  is a strict minimum of
is a strict minimum of  . So we can conclude that
. So we can conclude that  is a strict minimum of
is a strict minimum of  on
on  .
.
Let us outline the line-search SQP-type algorithm that uses the merit function  defined in (3.14) and the parameter updating scheme from [14], which is a generalized version to the algorithm in [2].
defined in (3.14) and the parameter updating scheme from [14], which is a generalized version to the algorithm in [2].
Algorithm 3.7.
Step 1.
Given a positive number  ,
,  ,
,  . Choose an initial iterate
. Choose an initial iterate  . Compute
. Compute  ,
,  ,
,  ,
,  ,
,  and
and . Set
. Set  .
.
Step 2.
If  , stop.
, stop.
Step 3.
Compute a symmetric matrix  and find a solution
and find a solution  to (3.12).
to (3.12).
Step 4.
Adapt  .
.
if
then
else
Step 5.
Compute

Using backtracking line search rule to compute the step length  :
:
Step 6.
set  ,
,  ;
;
Step 7.
if

holds for  , then
, then  and stop the line search.
and stop the line search.
Step 8.
else, choose  ;
;
Step 9.
set  , go to step 7
, go to step 7
Step 10.
Set  ,
,  ,
,  .
.
Step 11.
Compute  and
and  . Set
. Set 
 and go to 2
and go to 2
Now we are in a position to state the global convergence of the line search SQP Algorithm 3.7, whose proof can be found in [2].
Theorem 3.8.
Suppose that  ,
,  ,
,  are continuously differentiable and their derivatives are Lipschitz continuous. Consider Algorithm 3.7, if positive definite matrices
are continuously differentiable and their derivatives are Lipschitz continuous. Consider Algorithm 3.7, if positive definite matrices  and
and  are bounded, then one of the following situations occurs:
are bounded, then one of the following situations occurs:
(i)the sequence  is unbounded, in which case
is unbounded, in which case  is also unbounded;
is also unbounded;
(ii)there exists an index  such that
such that  for any
for any  , and one of the following situations occurs:
, and one of the following situations occurs:
(a)
(b) and
and  .
.
References
Fares B, Noll D, Apkarian P: Robust control via sequential semidefinite programming. SIAM Journal on Control and Optimization 2002,40(6):1791–1820. 10.1137/S0363012900373483
Correa R, Ramirez HC: A global algorithm for nonlinear semidefinite programming. SIAM Journal on Optimization 2004,15(1):303–318. 10.1137/S1052623402417298
Kočvara M, Stingl M: Pennon: a code for convex nonlinear and semidefinite programming. Optimization Methods & Software 2003,18(3):317–333. 10.1080/1055678031000098773
Kočvara M, Stingl M: Solving nonconvex SDP problems of structural optimization with stability control. Optimization Methods & Software 2004,19(5):595–609. 10.1080/10556780410001682844
Sun D, Sun J, Zhang L: The rate of convergence of the augmented Lagrangian method for nonlinear semidefinite programming. Mathematical Programming 2008.
Noll D: Local convergence of an augmented Lagrangian method for matrix inequality constrained programming. Optimization Methods and Software 2007,22(5):777–802. 10.1080/10556780701223970
Sun D: The strong second-order sufficient condition and constraint nondegeneracy in nonlinear semidefinite programming and their implications. Mathematics of Operations Research 2006,31(4):761–776. 10.1287/moor.1060.0195
Mifflin R: Semismooth and semiconvex functions in constrained optimization. SIAM Journal on Control and Optimization 1977,15(6):959–972. 10.1137/0315061
Qi LQ, Sun J: A nonsmooth version of Newton's method. Mathematical Programming 1993,58(1–3):353–367.
Zarantonello EH: Projections on convex sets in Hilbert space and spectral theory—I: projections on convex sets. In Contributions to Nonlinear Functional Analysis (Proceedings of a Symposium held at the Mathematics Research Center, University of Wisconsin, Madison, Wis., 1971). Edited by: Zarantonello EH. Academic Press, New York, NY, USA; 1971:237–341.
Zarantonello EH: Projections on convex sets in Hilbert space and spectral theory—II: spectral theory. In Contributions to Nonlinear Functional Analysis (Proceedings of a Symposium held at the Mathematics Research Center, University of Wisconsin, Madison, Wis., 1971). Edited by: Zarantonello EH. Academic Press, New York, NY, USA; 1971:343–424.
Sun D, Sun J: Semismooth matrix-valued functions. Mathematics of Operations Research 2002,27(1):150–169. 10.1287/moor.27.1.150.342
Bonnans JF, Shapiro A: Perturbation Analysis of Optimization Problems, Springer Series in Operations Research. Springer, New York, NY, USA; 2000:xviii+601.
Bonnans JF, Gilbert JC, Lemaréchal C, Sagastizábal CA: Numerical Optimization. Theoretical and Practical Aspects, Universitext. Springer, Berlin, Germany; 2003:xiv+419.
Acknowledgments
The research is supported by the National Natural Science Foundation of China under Project no. 10771026 and by the Scientific Research Foundation for the Returned Overseas Chinese Scholars, State Education Ministry of China.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, Y., Zhang, S. & Zhang, L. A Note on Convergence Analysis of an SQP-Type Method for Nonlinear Semidefinite Programming. J Inequal Appl 2008, 218345 (2007). https://doi.org/10.1155/2008/218345
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/218345
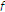 ,
, 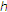 ,
, 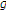 have a directional derivative at
have a directional derivative at  in the direction
in the direction 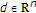 , then
, then  has also a directional derivative at
has also a directional derivative at  in the direction
in the direction 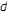 . If, in addition,
. If, in addition,  is feasible for (1.1), we have
is feasible for (1.1), we have