- Research Article
- Open access
- Published:
Schur-Type Inequalities for Complex Polynomials with no Zeros in the Unit Disk
Journal of Inequalities and Applications volume 2007, Article number: 090526 (2007)
Abstract
Starting out from a question posed by T. Erdélyi and J. Szabados, we consider Schur-type inequalities for the classes of complex algebraic polynomials having no zeros within the unit disk . The class of polynomials with no zeros in
. The class of polynomials with no zeros in —also known as Bernstein or Lorentz class—was studied in detail earlier. For real polynomials utilizing the Bernstein-Lorentz representation as convex combinations of fundamental polynomials
—also known as Bernstein or Lorentz class—was studied in detail earlier. For real polynomials utilizing the Bernstein-Lorentz representation as convex combinations of fundamental polynomials , G. Lorentz, T. Erdélyi, and J. Szabados proved a number of improved versions of Schur- (and also Bernstein- and Markov-) type inequalities. Here we investigate the similar questions for complex polynomials. For complex polynomials, the above convex representation is not available. Even worse, the set of complex polynomials, having no zeros in the unit disk, does not form a convex set. Therefore, a possible proof must go along different lines. In fact, such a direct argument was asked for by Erdélyi and Szabados already for the real case. The sharp forms of the Bernstein- and Markov-type inequalities are known, and the right factors are worse for complex coefficients than for real ones. However, here it turns out that Schur-type inequalities hold unchanged even for complex polynomials and for all monotonic, continuous weight functions. As a consequence, it becomes possible to deduce the corresponding Markov inequality from the known Bernstein inequality and the new Schur-type inequality with logarithmic weight.
, G. Lorentz, T. Erdélyi, and J. Szabados proved a number of improved versions of Schur- (and also Bernstein- and Markov-) type inequalities. Here we investigate the similar questions for complex polynomials. For complex polynomials, the above convex representation is not available. Even worse, the set of complex polynomials, having no zeros in the unit disk, does not form a convex set. Therefore, a possible proof must go along different lines. In fact, such a direct argument was asked for by Erdélyi and Szabados already for the real case. The sharp forms of the Bernstein- and Markov-type inequalities are known, and the right factors are worse for complex coefficients than for real ones. However, here it turns out that Schur-type inequalities hold unchanged even for complex polynomials and for all monotonic, continuous weight functions. As a consequence, it becomes possible to deduce the corresponding Markov inequality from the known Bernstein inequality and the new Schur-type inequality with logarithmic weight.
References
Borwein P, Erdélyi T: Polynomials and Polynomial Inequalities, Graduate Texts in Mathematics. Volume 161. Springer, New York, NY, USA; 1995:x+480.
Milovanović GV, Mitrinović DS, Rassias ThM: Topics in Polynomials: Extremal Problems, Inequalities, Zeros. World Scientific, River Edge, NJ, USA; 1994:xiv+821.
Pólya Gy, Szegö G: Aufgaben und Lehrsätze aus der Analysis, Vol. II, Die Grundlehren der matehmatischen Wissenschaften in Einzeldarstellungen. Volume 20. Springer, Berlin, Germany; 1925.
Lorentz GG: The degree of approximation by polynomials with positive coefficients. Mathematische Annalen 1963,151(3):239–251. 10.1007/BF01398235
Erdélyi T: Estimates for the Lorentz degree of polynomials. Journal of Approximation Theory 1991,67(2):187–198. 10.1016/0021-9045(91)90017-5
Kopotun KA: Uniform estimates of monotone and convex approximation of smooth functions. Journal of Approximation Theory 1995,80(1):76–107. 10.1006/jath.1995.1005
Kopotun KA, Leviatan D, Shevchuk IA: Convex polynomial approximation in the uniform norm: conclusion. Canadian Journal of Mathematics 2005,57(6):1224–1248. 10.4153/CJM-2005-049-6
Kopotun K, Leviatan D, Shevchuk IA: Coconvex approximation in the uniform norm: the final frontier. Acta Mathematica Hungarica 2006,110(1–2):117–151. 10.1007/s10474-006-0010-3
Polyrakis IA: Finite-dimensional lattice-subspaces of
 and curves of
and curves of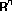 . Transactions of the American Mathematical Society 1996,348(7):2793–2810. 10.1090/S0002-9947-96-01639-X
. Transactions of the American Mathematical Society 1996,348(7):2793–2810. 10.1090/S0002-9947-96-01639-XPolyrakis IA: Lattice-subspaces of
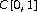 and positive bases. Journal of Mathematical Analysis and Applications 1994,184(1):1–18. 10.1006/jmaa.1994.1178
and positive bases. Journal of Mathematical Analysis and Applications 1994,184(1):1–18. 10.1006/jmaa.1994.1178Polyrakis IA: Minimal lattice-subspaces. Transactions of the American Mathematical Society 1999,351(10):4183–4203. 10.1090/S0002-9947-99-02384-3
Farkas B, Révész SGy: Positive bases in spaces of Polynomials. preprint, 2007 http://arxiv.org/abs/0708.2883 preprint, 2007
Erdélyi T, Szabados J: On polynomials with positive coefficients. Journal of Approximation Theory 1988,54(1):107–122. 10.1016/0021-9045(88)90119-0
Scheick JT: Inequalities for derivatives of polynomials of special type. Journal of Approximation Theory 1972,6(4):354–358. 10.1016/0021-9045(72)90041-X
Erdélyi T: Markov-Bernstein type inequalities for constrained polynomials with real versus complex coefficients. Journal d'Analyse Mathématique 1998, 74: 165–181.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Révész, S.G. Schur-Type Inequalities for Complex Polynomials with no Zeros in the Unit Disk. J Inequal Appl 2007, 090526 (2007). https://doi.org/10.1155/2007/90526
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/90526
 and curves of
and curves of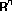 . Transactions of the American Mathematical Society 1996,348(7):2793–2810. 10.1090/S0002-9947-96-01639-X
. Transactions of the American Mathematical Society 1996,348(7):2793–2810. 10.1090/S0002-9947-96-01639-X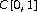 and positive bases. Journal of Mathematical Analysis and Applications 1994,184(1):1–18. 10.1006/jmaa.1994.1178
and positive bases. Journal of Mathematical Analysis and Applications 1994,184(1):1–18. 10.1006/jmaa.1994.1178