- Research Article
- Open access
- Published:
Extinction and Decay Estimates of Solutions for a Class of Porous Medium Equations
Journal of Inequalities and Applications volume 2007, Article number: 087650 (2007)
Abstract
The extinction phenomenon of solutions for the homogeneous Dirichlet boundary value problem of the porous medium equation , is studied. Sufficient conditions about the extinction and decay estimates of solutions are obtained by using
, is studied. Sufficient conditions about the extinction and decay estimates of solutions are obtained by using -integral model estimate methods and two crucial lemmas on differential inequality.
-integral model estimate methods and two crucial lemmas on differential inequality.
References
Ferreira R, Vazquez JL: Extinction behaviour for fast diffusion equations with absorption. Nonlinear Analysis: Theory, Methods & Applications 2001,43(8):943–985. 10.1016/S0362-546X(99)00178-9
Leoni G: A very singular solution for the porous media equation
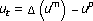 when
when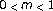 . Journal of Differential Equations 1996,132(2):353–376. 10.1006/jdeq.1996.0184
. Journal of Differential Equations 1996,132(2):353–376. 10.1006/jdeq.1996.0184Peletier LA, Zhao JN: Source-type solutions of the porous media equation with absorption: the fast diffusion case. Nonlinear Analysis: Theory, Methods & Applications 1990,14(2):107–121. 10.1016/0362-546X(90)90018-C
Li Y, Wu J: Extinction for fast diffusion equations with nonlinear sources. Electronic Journal of Differential Equations 2005,2005(23):1–7.
Anderson JR: Local existence and uniqueness of solutions of degenerate parabolic equations. Communications in Partial Differential Equations 1991,16(1):105–143. 10.1080/03605309108820753
Anderson JR: Necessary and sufficient conditions for the unique solvability of a nonlinear reaction-diffusion model. Journal of Mathematical Analysis and Applications 1998,228(2):483–494. 10.1006/jmaa.1998.6165
Chen SL: The extinction behavior of the solutions for a class of reaction-diffusion equations. Applied Mathematics and Mechanics 2001,22(11):1352–1356.
Chen SL: The extinction behavior of solutions for a reaction-diffusion equation. Journal of Mathematical Research and Exposition 1998,18(4):583–586.
Liu W: Periodic solutions of evolution-laplacian equations with a nonlinear convection term. International Journal of Mathematics and Mathematical Sciences 2007, 2007: 10 pages.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Liu, W., Wang, M. & Wu, B. Extinction and Decay Estimates of Solutions for a Class of Porous Medium Equations. J Inequal Appl 2007, 087650 (2007). https://doi.org/10.1155/2007/87650
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/87650
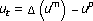 when
when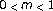 . Journal of Differential Equations 1996,132(2):353–376. 10.1006/jdeq.1996.0184
. Journal of Differential Equations 1996,132(2):353–376. 10.1006/jdeq.1996.0184