- Research Article
- Open access
- Published:
Some Geometric Inequalities in a New Banach Sequence Space
Journal of Inequalities and Applications volume 2007, Article number: 086757 (2007)
Abstract
The difference sequence space , which is a generalization of the space
, which is a generalization of the space introduced and studied by Sargent (1960), was defined by Çolak and Et (2005). In this paper we establish some geometric inequalities for this space.
introduced and studied by Sargent (1960), was defined by Çolak and Et (2005). In this paper we establish some geometric inequalities for this space.
References
Sargent WLC: Some sequence spaces related to the
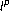 spaces. Journal of the London Mathematical Society 1960,35(2):161–171. 10.1112/jlms/s1-35.2.161
spaces. Journal of the London Mathematical Society 1960,35(2):161–171. 10.1112/jlms/s1-35.2.161Malkowsky E, Mursaleen M: Matrix transformations between FK-spaces and the sequence spaces
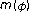 and
and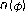 . Journal of Mathematical Analysis and Applications 1995,196(2):659–665. 10.1006/jmaa.1995.1432
. Journal of Mathematical Analysis and Applications 1995,196(2):659–665. 10.1006/jmaa.1995.1432Mursaleen M: Some geometric properties of a sequence space related to. Bulletin of the Australian Mathematical Society 2003,67(2):343–347. 10.1017/S0004972700033803
Tripathy BC, Sen M: On a new class of sequences related to the space. Tamkang Journal of Mathematics 2002,33(2):167–171.
Çolak R, Et M: On some difference sequence sets and their topological properties. Bulletin of the Malaysian Mathematical Sciences Society 2005,28(2):125–130.
Et M, Çolak R: On some generalized difference sequence spaces. Soochow Journal of Mathematics 1995,21(4):377–386.
Kı zmaz H: On certain sequence spaces. Canadian Mathematical Bulletin 1981,24(2):169–176. 10.4153/CMB-1981-027-5
Malkowsky E, Mursaleen M, Suantai S: The dual spaces of sets of difference sequences of orderand matrix transformations. Acta Mathematica Sinica 2007,23(3):521–532. 10.1007/s10114-005-0719-x
Cui Y, Hudzik H: On the Banach-Saks and weak Banach-Saks properties of some Banach sequence spaces. Acta Scientiarum Mathematicarum 1999,65(1–2):179–187.
Gurariĭ VI: Differential properties of the convexity moduli of Banach spaces. Matematicheskie Issledovaniya 1967,2(1):141–148.
Sánchez L, Ullán A: Some properties of Gurarii's modulus of convexity. Archiv der Mathematik 1998,71(5):399–406. 10.1007/s000130050283
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Mursaleen, M., Çolak, R. & Et, M. Some Geometric Inequalities in a New Banach Sequence Space. J Inequal Appl 2007, 086757 (2007). https://doi.org/10.1155/2007/86757
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/86757
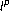 spaces. Journal of the London Mathematical Society 1960,35(2):161–171. 10.1112/jlms/s1-35.2.161
spaces. Journal of the London Mathematical Society 1960,35(2):161–171. 10.1112/jlms/s1-35.2.161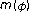 and
and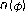 . Journal of Mathematical Analysis and Applications 1995,196(2):659–665. 10.1006/jmaa.1995.1432
. Journal of Mathematical Analysis and Applications 1995,196(2):659–665. 10.1006/jmaa.1995.1432