- Research Article
- Open access
- Published:
Sufficient Univalence Conditions for Analytic Functions
Journal of Inequalities and Applications volume 2007, Article number: 086493 (2008)
Abstract
We consider a general integral operator and the class of analytic functions. We extend some univalent conditions of Becker's type for analytic functions using a general integral transform.
References
Pescar V: A new generalization of Ahlfors's and Becker's criterion of univalence. Bulletin of the Malaysian Mathematical Society 1996,19(2):53–54.
Ozaki S, Nunokawa M: The Schwarzian derivative and univalent functions. Proceedings of the American Mathematical Society 1972,33(2):392–394. 10.1090/S0002-9939-1972-0299773-3
Nehari Z: Conformal Mapping. McGraw-Hill, New York, NY, USA; 1952:viii+396.
Nehari Z: Conformal Mapping. Dover, New York, NY, USA; 1975:vii+396.
Seenivasagan N, Breaz D: Certain sufficient conditions for univalence. to appear in General Mathematics to appear in General Mathematics
Breaz D, Breaz N: The univalent conditions for an integral operator on the calsses
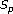 and
and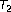 . Journal of Approximation Theory and Applications 2005,1(2):93–98.
. Journal of Approximation Theory and Applications 2005,1(2):93–98.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Breaz, D., Breaz, N. Sufficient Univalence Conditions for Analytic Functions. J Inequal Appl 2007, 086493 (2008). https://doi.org/10.1155/2007/86493
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/86493
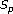 and
and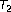 . Journal of Approximation Theory and Applications 2005,1(2):93–98.
. Journal of Approximation Theory and Applications 2005,1(2):93–98.