- Research Article
- Open access
- Published:
On the Strengthened Jordan's Inequality
Journal of Inequalities and Applications volume 2007, Article number: 074328 (2008)
Abstract
The main purpose of this paper is to present two methods of sharpening Jordan's inequality. The first method shows that one can obtain new strengthened Jordan's inequalities from old ones. The other method shows that one can sharpen Jordan's inequality by choosing proper functions in the monotone form of L'Hopital's rule. Finally, we improve a related inequality proposed early by Redheffer.
References
Mitrinović DS: Analytic Inequalities. Springer, New York, NY, USA; 1970:xii+400.
Debnath L, Zhao C-J: New strengthened Jordan's inequality and its applications. Applied Mathematics Letters 2003,16(4):557–560. 10.1016/S0893-9659(03)00036-3
Mercer AMcD, Abel U, Caccia D: Problems and solutions: solutions of elementary problems: E2952. The American Mathematical Monthly 1986,93(7):568–569. 10.2307/2323042
Özban AY: A new refined form of Jordan's inequality and its applications. Applied Mathematics Letters 2006,19(2):155–160. 10.1016/j.aml.2005.05.003
Anderson GD, Qiu S-L, Vamanamurthy MK, Vuorinen M: Generalized elliptic integrals and modular equations. Pacific Journal of Mathematics 2000,192(1):1–37. 10.2140/pjm.2000.192.1
Zhu L: Sharpening Jordan's inequality and the Yang Le inequality. Applied Mathematics Letters 2006,19(3):240–243. 10.1016/j.aml.2005.06.004
Zhu L: Sharpening Jordan's inequality and Yang Le inequality—II. Applied Mathematics Letters 2006,19(9):990–994. 10.1016/j.aml.2005.11.011
Wu S, Debnath L: A new generalized and sharp version of Jordan's inequality and its applications to the improvement of the Yang Le inequality. Applied Mathematics Letters 2006,19(12):1378–1384. 10.1016/j.aml.2006.02.005
Wu S, Debnath L: A new generalized and sharp version of Jordan's inequality and its applications to the improvement of the Yang Le inequality—II. Applied Mathematics Letters 2007,20(5):532–538. 10.1016/j.aml.2006.05.022
Li J-L: An identity related to Jordan's inequality. International Journal of Mathematics and Mathematical Sciences 2006, 2006: 6 pages.
Redheffer R, Ungar P, Lupas A, et al.: Problems and solutions: advanced problems: 5642,5665–5670. The American Mathematical Monthly 1969,76(4):422–423. 10.2307/2316453
Williams JP: Problems and solutions: solutions of advanced problems: 5642. The American Mathematical Monthly 1969,76(10):1153–1154.
Li J-L: On a series of Erdős-Turán type. Analysis 1992,12(3–4):315–317.
Young RM: An Introduction to Nonharmonic Fourier Series, Pure and Applied Mathematics. Volume 93. Academic Press, New York, NY, USA; 1980:x+246.
Li J-L: Spectral self-affine measures in
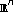 . Proceedings of the Edinburgh Mathematical Society 2007,50(1):197–215. 10.1017/S0013091503000324
. Proceedings of the Edinburgh Mathematical Society 2007,50(1):197–215. 10.1017/S0013091503000324
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, JL., Li, YL. On the Strengthened Jordan's Inequality. J Inequal Appl 2007, 074328 (2008). https://doi.org/10.1155/2007/74328
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/74328
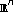 . Proceedings of the Edinburgh Mathematical Society 2007,50(1):197–215. 10.1017/S0013091503000324
. Proceedings of the Edinburgh Mathematical Society 2007,50(1):197–215. 10.1017/S0013091503000324