- Research Article
- Open access
- Published:
Oscillatory Property of Solutions for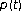 -Laplacian Equations
-Laplacian Equations
Journal of Inequalities and Applications volume 2007, Article number: 058548 (2007)
Abstract
We consider the oscillatory property of the following -Laplacian equations
-Laplacian equations ,
, . Since there is no Picone-type identity for
. Since there is no Picone-type identity for - Laplacian equations, it is an unsolved problem that whether the Sturmian comparison theorems for
- Laplacian equations, it is an unsolved problem that whether the Sturmian comparison theorems for -Laplacian equations are valid or not. We obtain sufficient conditions of the oscillatory of solutions for
-Laplacian equations are valid or not. We obtain sufficient conditions of the oscillatory of solutions for -Laplacian equations.
-Laplacian equations.
References
Acerbi E, Mingione G: Regularity results for stationary electro-rheological fluids. Archive for Rational Mechanics and Analysis 2002,164(3):213–259. 10.1007/s00205-002-0208-7
Fan X, Zhang QH, Zhao D: Eigenvalues of-Laplacian Dirichlet problem. Journal of Mathematical Analysis and Applications 2005,302(2):306–317. 10.1016/j.jmaa.2003.11.020
Růžička M: Electrorheological Fluids: Modeling and Mathematical Theory, Lecture Notes in Mathematics. Volume 1748. Springer, Berlin, Germany; 2000:xvi+176.
Zhang QH: A strong maximum principle for differential equations with nonstandard-growth conditions. Journal of Mathematical Analysis and Applications 2005,312(1):24–32. 10.1016/j.jmaa.2005.03.013
Zhang QH: The asymptotic behavior of solutions for-laplace equations. to appear in Journal of Zhengzhou University of Light to appear in Journal of Zhengzhou University of Light
Zhikov VV: Averaging of functionals of the calculus of variations and elasticity theory. Mathematics of the USSR. Izvestija 1987,29(1):33–36. 10.1070/IM1987v029n01ABEH000958
Agarwal RP, Grace SR: On the oscillation of certain second order differential equations. Georgian Mathematical Journal 2000,7(2):201–213.
Jaroš J, Takaŝi K, Yoshida N: Picone-type inequalities for nonlinear elliptic equations with first-order terms and their applications. Journal of Inequalities and Applications 2006, 2006: 17 pages.
Lorca S: Nonexistence of positive solution for quasilinear elliptic problems in the half-space. Journal of Inequalities and Applications 2007, 2007: 4 pages.
Sugie J, Yamaoka N: Growth conditions for oscillation of nonlinear differential equations with-Laplacian. Journal of Mathematical Analysis and Applications 2005,306(1):18–34. 10.1016/j.jmaa.2004.10.009
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, Q. Oscillatory Property of Solutions for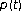 -Laplacian Equations.
J Inequal Appl 2007, 058548 (2007). https://doi.org/10.1155/2007/58548
-Laplacian Equations.
J Inequal Appl 2007, 058548 (2007). https://doi.org/10.1155/2007/58548
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/58548