- Research Article
- Open access
- Published:
A Hardy Inequality with Remainder Terms in the Heisenberg Group and the Weighted Eigenvalue Problem
Journal of Inequalities and Applications volume 2007, Article number: 032585 (2007)
Abstract
Based on properties of vector fields, we prove Hardy inequalities with remainder terms in the Heisenberg group and a compact embedding in weighted Sobolev spaces. The best constants in Hardy inequalities are determined. Then we discuss the existence of solutions for the nonlinear eigenvalue problems in the Heisenberg group with weights for the -sub-Laplacian. The asymptotic behaviour, simplicity, and isolation of the first eigenvalue are also considered.
-sub-Laplacian. The asymptotic behaviour, simplicity, and isolation of the first eigenvalue are also considered.
References
Capogna L, Danielli D, Garofalo N: An embedding theorem and the Harnack inequality for nonlinear subelliptic equations. Communications in Partial Differential Equations 1993,18(9–10):1765–1794.
Domokos A, Manfredi JJ:
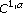 -regularity for
-regularity for -harmonic functions in the Heisenberg group for
-harmonic functions in the Heisenberg group for near 2. In The p-Harmonic Equation and Recent Advances in Analysis, Contemporary Mathematics. Volume 370. American Mathematical Society, Providence, RI, USA; 2005:17–23.
near 2. In The p-Harmonic Equation and Recent Advances in Analysis, Contemporary Mathematics. Volume 370. American Mathematical Society, Providence, RI, USA; 2005:17–23.Allegretto W: Principal eigenvalues for indefinite-weight elliptic problems in
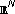 . Proceedings of the American Mathematical Society 1992,116(3):701–706.
. Proceedings of the American Mathematical Society 1992,116(3):701–706.Adimurthi , Chaudhuri N, Ramaswamy M: An improved Hardy-Sobolev inequality and its application. Proceedings of the American Mathematical Society 2002,130(2):489–505. 10.1090/S0002-9939-01-06132-9
Chaudhuri N, Ramaswamy M: Existence of positive solutions of some semilinear elliptic equations with singular coefficients. Proceedings of the Royal Society of Edinburgh: Section A 2001,131(6):1275–1295. 10.1017/S0308210500001396
Adimurthi , Esteban MJ: An improved Hardy-Sobolev inequality in
 and its application to Schrödinger operators. Nonlinear Differential Equations and Applications 2005,12(2):243–263. 10.1007/s00030-005-0009-4
and its application to Schrödinger operators. Nonlinear Differential Equations and Applications 2005,12(2):243–263. 10.1007/s00030-005-0009-4García Azorero JP, Peral Alonso I: Hardy inequalities and some critical elliptic and parabolic problems. Journal of Differential Equations 1998,144(2):441–476. 10.1006/jdeq.1997.3375
Lê A: Eigenvalue problems for the
 -Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2006,64(5):1057–1099. 10.1016/j.na.2005.05.056
-Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2006,64(5):1057–1099. 10.1016/j.na.2005.05.056Vázquez JL, Zuazua E: The Hardy inequality and the asymptotic behaviour of the heat equation with an inverse-square potential. Journal of Functional Analysis 2000,173(1):103–153. 10.1006/jfan.1999.3556
De Napoli PL, Pinasco JP: Eigenvalues of the
 -Laplacian and disconjugacy criteria. Journal of Inequalities and Applications 2006, 2006: 8 pages.
-Laplacian and disconjugacy criteria. Journal of Inequalities and Applications 2006, 2006: 8 pages.Jaroš J, Takaŝi K, Yoshida N: Picone-type inequalities for nonlinear elliptic equations and their applications. Journal of Inequalities and Applications 2001,6(4):387–404. 10.1155/S1025583401000236
Yaotian S, Zhihui C: General Hardy inequalities with optimal constants and remainder terms. Journal of Inequalities and Applications 2005, (3):207–219.
Barbatis G, Filippas S, Tertikas A: A unified approach to improved
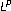 Hardy inequalities with best constants. Transactions of the American Mathematical Society 2004,356(6):2169–2196. 10.1090/S0002-9947-03-03389-0
Hardy inequalities with best constants. Transactions of the American Mathematical Society 2004,356(6):2169–2196. 10.1090/S0002-9947-03-03389-0Barbatis G, Filippas S, Tertikas A: Series expansion for
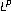 Hardy inequalities. Indiana University Mathematics Journal 2003,52(1):171–190. 10.1512/iumj.2003.52.2207
Hardy inequalities. Indiana University Mathematics Journal 2003,52(1):171–190. 10.1512/iumj.2003.52.2207Niu P, Zhang H, Wang Y: Hardy type and Rellich type inequalities on the Heisenberg group. Proceedings of the American Mathematical Society 2001,129(12):3623–3630. 10.1090/S0002-9939-01-06011-7
D'Ambrosio L: Critical degenerate inequalities on the Heisenberg group. Manuscripta Mathematica 2001,106(4):519–536. 10.1007/s229-001-8031-2
D'Ambrosio L: Hardy-type inequalities related to degenerate elliptic differential operators. Annali della Scuola Normale Superiore di Pisa 2005,4(3):451–486.
Garofalo N, Nhieu D-M: Isoperimetric and Sobolev inequalities for Carnot-Carathéodory spaces and the existence of mimimal surfaces. Communications on Pure and Applied Mathematics 1996,49(10):1081–1144. 10.1002/(SICI)1097-0312(199610)49:10<1081::AID-CPA3>3.0.CO;2-A
Struwe M: Variational Methods: Applications to Nonlinear Partial Differential Equations and Hamiltonian Systems, A Series of Modern Surveys in Mathematics. Volume 34. 3rd edition. Springer, Berlin, Germany; 2000:xviii+274.
Boccardo L, Murat F: Almost everywhere convergence of the gradients of solutions to elliptic and parabolic equations. Nonlinear Analysis: Theory, Methods & Applications 1992,19(6):581–597. 10.1016/0362-546X(92)90023-8
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Dou, J., Niu, P. & Yuan, Z. A Hardy Inequality with Remainder Terms in the Heisenberg Group and the Weighted Eigenvalue Problem. J Inequal Appl 2007, 032585 (2007). https://doi.org/10.1155/2007/32585
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/32585
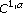 -regularity for
-regularity for -harmonic functions in the Heisenberg group for
-harmonic functions in the Heisenberg group for near 2. In The p-Harmonic Equation and Recent Advances in Analysis, Contemporary Mathematics. Volume 370. American Mathematical Society, Providence, RI, USA; 2005:17–23.
near 2. In The p-Harmonic Equation and Recent Advances in Analysis, Contemporary Mathematics. Volume 370. American Mathematical Society, Providence, RI, USA; 2005:17–23.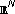 . Proceedings of the American Mathematical Society 1992,116(3):701–706.
. Proceedings of the American Mathematical Society 1992,116(3):701–706. and its application to Schrödinger operators. Nonlinear Differential Equations and Applications 2005,12(2):243–263. 10.1007/s00030-005-0009-4
and its application to Schrödinger operators. Nonlinear Differential Equations and Applications 2005,12(2):243–263. 10.1007/s00030-005-0009-4 -Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2006,64(5):1057–1099. 10.1016/j.na.2005.05.056
-Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2006,64(5):1057–1099. 10.1016/j.na.2005.05.056 -Laplacian and disconjugacy criteria. Journal of Inequalities and Applications 2006, 2006: 8 pages.
-Laplacian and disconjugacy criteria. Journal of Inequalities and Applications 2006, 2006: 8 pages.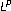 Hardy inequalities with best constants. Transactions of the American Mathematical Society 2004,356(6):2169–2196. 10.1090/S0002-9947-03-03389-0
Hardy inequalities with best constants. Transactions of the American Mathematical Society 2004,356(6):2169–2196. 10.1090/S0002-9947-03-03389-0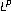 Hardy inequalities. Indiana University Mathematics Journal 2003,52(1):171–190. 10.1512/iumj.2003.52.2207
Hardy inequalities. Indiana University Mathematics Journal 2003,52(1):171–190. 10.1512/iumj.2003.52.2207