- Research Article
- Open access
- Published:
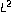 -Boundedness of Marcinkiewicz Integrals along Surfaces with Variable Kernels: Another Sufficient Condition
-Boundedness of Marcinkiewicz Integrals along Surfaces with Variable Kernels: Another Sufficient Condition
Journal of Inequalities and Applications volume 2007, Article number: 026765 (2007)
Abstract
We give the estimates for the Marcinkiewicz integral with rough variable kernels associated to surfaces. More precisely, we give some other sufficient conditions which are different from the conditions known before to warrant that the
estimates for the Marcinkiewicz integral with rough variable kernels associated to surfaces. More precisely, we give some other sufficient conditions which are different from the conditions known before to warrant that the -boundedness holds. As corollaries of this result, we show that similar properties still hold for parametric Littlewood-Paley area integral and parametric
-boundedness holds. As corollaries of this result, we show that similar properties still hold for parametric Littlewood-Paley area integral and parametric functions with rough variable kernels. Some of the results are extensions of some known results.
functions with rough variable kernels. Some of the results are extensions of some known results.
References
Calderón AP, Zygmund A: On a problem of Mihlin. Transactions of the American Mathematical Society 1955,78(1):209–224.
Aguilera NE, Harboure EO: Some inequalities for maximal operators. Indiana University Mathematics Journal 1980,29(4):559–576. 10.1512/iumj.1980.29.29042
Tang L, Yang D: Boundedness of singular integrals of variable rough Calderón-Zygmund kernels along surfaces. Integral Equations and Operator Theory 2002,43(4):488–502. 10.1007/BF01212707
Stein EM: On the functions of Littlewood-Paley, Lusin, and Marcinkiewicz. Transactions of the American Mathematical Society 1958,88(2):430–466. 10.1090/S0002-9947-1958-0112932-2
Ding Y, Fan D, Pan Y: Weighted boundedness for a class of rough Marcinkiewicz integrals. Indiana University Mathematics Journal 1999,48(3):1037–1055.
Ding Y, Fan D, Pan Y:
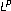 -boundedness of Marcinkiewicz integrals with Hardy space function kernels. Acta Mathematica Sinica 2000,16(4):593–600. 10.1007/s101140000015
-boundedness of Marcinkiewicz integrals with Hardy space function kernels. Acta Mathematica Sinica 2000,16(4):593–600. 10.1007/s101140000015Fan D, Sato S: Weak type
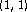 estimates for Marcinkiewicz integrals with rough kernels. Tohoku Mathematical Journal 2001,53(2):265–284. 10.2748/tmj/1178207481
estimates for Marcinkiewicz integrals with rough kernels. Tohoku Mathematical Journal 2001,53(2):265–284. 10.2748/tmj/1178207481Ding Y, Lin C-C, Shao S: On the Marcinkiewicz integral with variable kernels. Indiana University Mathematics Journal 2004,53(3):805–821. 10.1512/iumj.2004.53.2406
Xue Q, Yabuta K:
 -boundedness of Marcinkiewicz integrals along surfaces with variable kernels. Scientiae Mathematicae Japonicae 2006,63(3):369–382.
-boundedness of Marcinkiewicz integrals along surfaces with variable kernels. Scientiae Mathematicae Japonicae 2006,63(3):369–382.Al-Qassem HM: On weighted inequalities for parametric Marcinkiewicz integrals. Journal of Inequalities and Applications 2006, 2006: 17 pages.
Stein EM, Weiss G: Introduction to Fourier Analysis on Euclidean Spaces, Princeton Mathematical Series, no. 32. Princeton University Press, Princeton, NJ, USA; 1971:x+297.
Xue Q, Yabuta K: Correction and addition to "
 -boundedness of Marcinkiewicz integrals along surfaces with variable kernels". Scientiae Mathematicae Japonicae 2007,65(2):291–298.
-boundedness of Marcinkiewicz integrals along surfaces with variable kernels". Scientiae Mathematicae Japonicae 2007,65(2):291–298.Lorch L, Szego P: A singular integral whose kernel involves a Bessel function. Duke Mathematical Journal 1955,22(3):407–418. 10.1215/S0012-7094-55-02244-4
Watson GN: A Treatise on the Theory of Bessel Functions. 2nd edition. Cambridge University Press, London, UK; 1966.
Calderón AP, Zygmund A: On singular integrals with variable kernels. Applicable Analysis 1978,7(3):221–238. 10.1080/00036817808839193
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xue, Q., Yabuta, K. 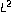 -Boundedness of Marcinkiewicz Integrals along Surfaces with Variable Kernels: Another Sufficient Condition.
J Inequal Appl 2007, 026765 (2007). https://doi.org/10.1155/2007/26765
-Boundedness of Marcinkiewicz Integrals along Surfaces with Variable Kernels: Another Sufficient Condition.
J Inequal Appl 2007, 026765 (2007). https://doi.org/10.1155/2007/26765
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/26765
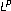 -boundedness of Marcinkiewicz integrals with Hardy space function kernels. Acta Mathematica Sinica 2000,16(4):593–600. 10.1007/s101140000015
-boundedness of Marcinkiewicz integrals with Hardy space function kernels. Acta Mathematica Sinica 2000,16(4):593–600. 10.1007/s101140000015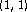 estimates for Marcinkiewicz integrals with rough kernels. Tohoku Mathematical Journal 2001,53(2):265–284. 10.2748/tmj/1178207481
estimates for Marcinkiewicz integrals with rough kernels. Tohoku Mathematical Journal 2001,53(2):265–284. 10.2748/tmj/1178207481 -boundedness of Marcinkiewicz integrals along surfaces with variable kernels. Scientiae Mathematicae Japonicae 2006,63(3):369–382.
-boundedness of Marcinkiewicz integrals along surfaces with variable kernels. Scientiae Mathematicae Japonicae 2006,63(3):369–382. -boundedness of Marcinkiewicz integrals along surfaces with variable kernels". Scientiae Mathematicae Japonicae 2007,65(2):291–298.
-boundedness of Marcinkiewicz integrals along surfaces with variable kernels". Scientiae Mathematicae Japonicae 2007,65(2):291–298.