- Research Article
- Open access
- Published:
About -Positivity Properties of Time-Invariant Linear Systems Subject to Point Delays
-Positivity Properties of Time-Invariant Linear Systems Subject to Point Delays
Journal of Inequalities and Applications volume 2007, Article number: 025872 (2007)
Abstract
This paper discusses nonnegativity and positivity concepts and related properties for the state and output trajectory solutions of dynamic linear time-invariant systems described by functional differential equations subject to point time delays. The various nonnegativities and positivities are introduced hierarchically from the weakest one to the strongest one while separating the corresponding properties when applied to the state space or to the output space as well as for the zero-initial state or zero-input responses. The formulation is first developed by defining cones for the input, state and output spaces of the dynamic system, and then extended, in particular, to cones being the three first orthants each being of the corresponding dimension of the input, state, and output spaces.
References
Agarwal RP, O'Regan D, Staněk S: Positive solutions of singular problems with sign changing Carathéodory nonlinearities depending on
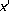 . Journal of Mathematical Analysis and Applications 2003,279(2):597–616. 10.1016/S0022-247X(03)00046-5
. Journal of Mathematical Analysis and Applications 2003,279(2):597–616. 10.1016/S0022-247X(03)00046-5Mainar E, Peña JM: Knot insertion and totally positive systems. Journal of Approximation Theory 2000,104(1):45–76. 10.1006/jath.1999.3438
Berman A, Plemmons RJ: Nonnegative Matrices in the Mathematical Sciences, Classics in Applied Mathematics. Volume 9. SIAM, Philadelphia, Pa, USA; 1994:xx+340.
Chen Y-Z: Omega limit sets in positive cones. Bulletin of the London Mathematical Society 2004,36(1):72–80. 10.1112/S0024609303002625
Li J, Whitaker J: Exceptional family of elements and solvability of variational inequalities for mappings defined only on closed convex cones in Banach spaces. Journal of Mathematical Analysis and Applications 2005,310(1):254–261. 10.1016/j.jmaa.2005.02.006
Jayanthan AV, Verma JK: Hilbert coefficients and depth of fiber cones. Journal of Pure and Applied Algebra 2005,201(1–3):97–115.
Kaczorek T: Positive 1D and 2D Systems, Series on Communications and Control Engineering, E.D. Sontag and M. Thoma eds.. Springer, Berlin, Germany; 2002.
Farina L, Rinaldi S: Positive Linear Systems. Theory and Applications, Pure and Applied Mathematics (New York). John Wiley & Sons, New York, NY, USA; 2000:x+305.
Bru R, Romero S, Sánchez E: Canonical forms for positive discrete-time linear control systems. Linear Algebra and Its Applications 2000,310(1–3):49–71.
Bru R, Romero S, Sánchez E: Structural properties of positive periodic discrete-time linear systems: canonical forms. Applied Mathematics and Computation 2004,153(3):697–719. 10.1016/S0096-3003(03)00665-9
Bru R, Coll C, Romero S, Sánchez E: Reachability indices of positive linear systems. Electronic Journal of Linear Algebra 2004, 11: 88–102.
Fornasini E, Valcher ME: Controllability and reachability of 2-D positive systems: a graph theoretic approach. IEEE Transactions on Circuits and Systems I. Regular Papers 2005,52(3):576–585.
Benvenuti L, Farina L: Eigenvalue regions for positive systems. Systems & Control Letters 2004,51(3–4):325–330. 10.1016/j.sysconle.2003.09.009
Agarwal RP, Perera K, O'Regan D: Positive solutions of higher-order singular problems. Differential Equations 2005,41(5):739–743. 10.1007/s10625-005-0209-z
Caccetta L, Rumchev VG: Reachable discrete-time positive systems with minimal dimension control sets. Dynamics of Continuous, Discrete and Impulsive Systems 1998,4(4):539–552.
De Leenheer P, Aeyels D: Stabilization of positive systems with first integrals. Automatica 2002,38(9):1583–1589. 10.1016/S0005-1098(02)00056-0
Diamond P, Opoitsev V: Absolute stability of positive systems with differential constraints. International Journal of Control 2000,73(3):210–218. 10.1080/002071700219759
Kaczorek T: Neural networks of positive systems. Proceedings of the 7th International Conference on Artificial Intelligence and Soft Computing (ICAISC '04), June 2004, Zakopane, Poland, Lecture Notes in Artificial Intelligence 3070: 56–63.
De la Sen M: Some conceptual links between dynamic physical systems and operator theory issues concerning energy balances and stability. Informatica 2005,16(3):395–406.
Fornasini E, Valcher ME: Directed graph,
 D state models, and characteristic polynomials of irreducible matrix pairs. Linear Algebra and Its Applications 1997,263(1–3):275–310.
D state models, and characteristic polynomials of irreducible matrix pairs. Linear Algebra and Its Applications 1997,263(1–3):275–310.Niu Y, Lam J, Wang X: Sliding-mode control for uncertain neutral delay systems. IEE Proceedings: Control Theory and Applications 2004,151(1):38–44. 10.1049/ip-cta:20040009
Coxson PG, Shapiro H: Positive input reachability and controllability of positive systems. Linear Algebra and Its Applications 1987, 94: 35–53. 10.1016/0024-3795(87)90076-0
Rumchev VG, James DJG: Controllability of positive linear discrete-time systems. International Journal of Control 1989,50(3):845–857. 10.1080/00207178908953401
Rumchev VG, James DJG: Spectral characterization and pole assignment for positive linear discrete-time systems. International Journal of Systems Science 1995,26(2):295–312.
Jafarov EM, Tasaltin R: Robust sliding-mode control for the uncertain MIMO aircraft model F-18. IEEE Transactions on Aerospace and Electronic Systems 2000,36(4):1127–1141. 10.1109/7.892663
Jafarov EM: Robust sliding mode controllers design techniques for stabilization of multivariable time-delay systems with parameter perturbations and external disturbances. International Journal of Systems Science 2005,36(7):433–444. 10.1080/00207720500156363
De la Sen M: Sufficiency-type stability and stabilization criteria for linear time-invariant systems with constant point delays. Acta Applicandae Mathematicae 2004,83(3):235–256.
De la Sen M: On pole-placement controllers for linear time-delay systems with commensurate point delays. Mathematical Problems in Engineering 2005,2005(1):123–140. 10.1155/MPE.2005.123
De la Sen M, Luo NS: On the uniform exponential stability of a wide class of linear time-delay systems. Journal of Mathematical Analysis and Applications 2004,289(2):456–476. 10.1016/j.jmaa.2003.08.048
Liu Z, Liao L: Existence and global exponential stability of periodic solution of cellular neural networks with time-varying delays. Journal of Mathematical Analysis and Applications 2004,290(1):247–262. 10.1016/j.jmaa.2003.09.052
Tang XH: Asymptotic behavior of a differential equation with distributed delays. Journal of Mathematical Analysis and Applications 2005,301(2):313–335. 10.1016/j.jmaa.2004.07.023
Pao CV: Stability and attractivity of periodic solutions of parabolic systems with time delays. Journal of Mathematical Analysis and Applications 2005,304(2):423–450. 10.1016/j.jmaa.2004.09.014
Liu S, Kouche M, Tatar N-E: Permanence extinction and global asymptotic stability in a stage structured system with distributed delays. Journal of Mathematical Analysis and Applications 2005,301(1):187–207. 10.1016/j.jmaa.2004.07.017
De la Sen M: Stability of impulsive time-varying systems and compactness of the operators mapping the input space into the state and output spaces. Journal of Mathematical Analysis and Applications 2006,321(2):621–650. 10.1016/j.jmaa.2005.08.038
Wong PJY, Agarwal RP: Oscillation criteria for nonlinear partial difference equations with delays. Computers & Mathematics with Applications 1996,32(6):57–86. 10.1016/0898-1221(96)00144-7
De la Sen M: Adaptive control of time-varying systems with time-varying delays. Dynamics of Continuous, Discrete & Impulsive Systems. Series A. Mathematical Analysis 2005,12(1):45–66.
Kaczorek T: Realization problem for positive continuous-time systems with delays. Proceedings of the 18th International Conference on Systems Engineering (ICSEng '05), August 2005, Las Vegas, Nev, USA
Haddad WM, Chellaboina V: Stability theory for nonnegative and compartmental dynamical systems with time delay. Systems & Control Letters 2004,51(5):355–361. 10.1016/j.sysconle.2003.09.006
Kaczorek T: Realization problem for positive discrete-time systems with delays. Systems Science 2004,30(4):17–30.
Bakule L, Paulet-Crainiceanu F, Rodellar J, Rossell JM: Overlapping reliable control for a cable-stayed bridge benchmark. IEEE Transactions on Control Systems Technology 2005,13(4):663–669.
Mañosa V, Ikhouane F, Rodellar J: Control of uncertain non-linear systems via adaptive backstepping. Journal of Sound and Vibration 2005,280(3–5):657–680.
Yi S, Ulsoy AG: Solution of a system of linear delay differential equations using the matrix Lambert function. Proceedings of the American Control Conference (ACC '06), June 2006, Minneapolis, Minn, USA 2433–2438.
Borisovich A, Marzantowicz W: Positive oriented periodic solutions of the first-order complex ODE with polynomial nonlinear part. Journal of Inequalities and Applications 2006, 2006: 21 pages.
Buescu J, Paixão AC: Inequalities for differentiable reproducing kernels and an application to positive integral operators. Journal of Inequalities and Applications 2006, 2006: 9 pages.
Long NT: On the nonexistence of positive solution of some singular nonlinear integral equations. Journal of Inequalities and Applications 2006, 2006: 10 pages.
De la Sen M: About the positivity of a class of hybrid dynamic linear systems. Applied Mathematics and Computation 2007,189(2):1199–1207.
De la Sen M: On positivity of singular regular linear time-delay time-invariant systems subject to multiple internal and external incommensurate point delays. to appear in Applied Mathematics and Computation to appear in Applied Mathematics and Computation
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
De la Sen, M. About -Positivity Properties of Time-Invariant Linear Systems Subject to Point Delays.
J Inequal Appl 2007, 025872 (2007). https://doi.org/10.1155/2007/25872
-Positivity Properties of Time-Invariant Linear Systems Subject to Point Delays.
J Inequal Appl 2007, 025872 (2007). https://doi.org/10.1155/2007/25872
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/25872
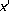 . Journal of Mathematical Analysis and Applications 2003,279(2):597–616. 10.1016/S0022-247X(03)00046-5
. Journal of Mathematical Analysis and Applications 2003,279(2):597–616. 10.1016/S0022-247X(03)00046-5 D state models, and characteristic polynomials of irreducible matrix pairs. Linear Algebra and Its Applications 1997,263(1–3):275–310.
D state models, and characteristic polynomials of irreducible matrix pairs. Linear Algebra and Its Applications 1997,263(1–3):275–310.