Skip to main content
Journal of Inequalities and Applications
Download PDF
  • Research Article
  • Open access
  • Published:

Existence and Asymptotic Behavior of Positive Solutions to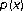-Laplacian Equations with Singular Nonlinearities

Journal of Inequalities and Applications volume 2007, Article number: 019349 (2007) Cite this article

Abstract

This paper investigates the-Laplacian equations with singular nonlinearities in, on, where is called-Laplacian. The existence of positive solutions is given, and the asymptotic behavior of solutions near boundary is discussed.

[123456789101112131415161718]

References

  1. Chen Y, Levine S, Rao M: Variable exponent, linear growth functionals in image restoration. SIAM Journal on Applied Mathematics 2006,66(4):1383–1406.

    Article  MathSciNet  Google Scholar 

  2. Rúzicka M: Electrorheological Fluids: Modeling and Mathematical Theory, Lecture Notes in Mathematics. Volume 1748. Springer, Berlin, Germany; 2000:xvi+176.

    Google Scholar 

  3. Fan X-L, Zhao D: On the spacesand. Journal of Mathematical Analysis and Applications 2001,263(2):424–446. 10.1006/jmaa.2000.7617

    Article  MathSciNet  MATH  Google Scholar 

  4. Fan X-L, Zhao D: The quasi-minimizer of integral functionals withgrowth conditions. Nonlinear Analysis: Theory, Methods & Applications 2000,39(7):807–816. 10.1016/S0362-546X(98)00239-9

    Article  MathSciNet  MATH  Google Scholar 

  5. Fan X-L, Zhang Q-H: Existence of solutions for-Laplacian Dirichlet problem. Nonlinear Analysis: Theory, Methods & Applications 2003,52(8):1843–1852. 10.1016/S0362-546X(02)00150-5

    Article  MathSciNet  MATH  Google Scholar 

  6. Fan X-L, Zhang Q, Zhao D: Eigenvalues of-Laplacian Dirichlet problem. Journal of Mathematical Analysis and Applications 2005,302(2):306–317. 10.1016/j.jmaa.2003.11.020

    Article  MathSciNet  MATH  Google Scholar 

  7. Fan X-L: Globalregularity for variable exponent elliptic equations in divergence form. Journal of Differential Equations 2007,235(2):397–417. 10.1016/j.jde.2007.01.008

    Article  MathSciNet  MATH  Google Scholar 

  8. Kováčik O, Rákosník J: On spacesand. Czechoslovak Mathematical Journal 1991,41(4):592–618.

    MathSciNet  Google Scholar 

  9. Marcellini P: Regularity and existence of solutions of elliptic equations with-growth conditions. Journal of Differential Equations 1991,90(1):1–30. 10.1016/0022-0396(91)90158-6

    Article  MathSciNet  MATH  Google Scholar 

  10. Zhang Q: A strong maximum principle for differential equations with nonstandard-growth conditions. Journal of Mathematical Analysis and Applications 2005,312(1):24–32. 10.1016/j.jmaa.2005.03.013

    Article  MathSciNet  MATH  Google Scholar 

  11. Zhang Q: Existence of positive solutions for a class of-Laplacian systems. Journal of Mathematical Analysis and Applications 2007,333(2):591–603. 10.1016/j.jmaa.2006.11.037

    Article  MathSciNet  MATH  Google Scholar 

  12. Zhang Q: Existence of positive solutions for elliptic systems with nonstandard-growth conditions via sub-supersolution method. Nonlinear Analysis: Theory, Methods & Applications 2007,67(4):1055–1067. 10.1016/j.na.2006.06.017

    Article  MathSciNet  MATH  Google Scholar 

  13. Zhang Q: Oscillatory property of solutions for-laplacian equations. Journal of Inequalities and Applications 2007, 2007: 8 pages.

    Google Scholar 

  14. Baxley JV: Some singular nonlinear boundary value problems. SIAM Journal on Mathematical Analysis 1991,22(2):463–479. 10.1137/0522030

    Article  MathSciNet  MATH  Google Scholar 

  15. Cui S: Existence and nonexistence of positive solutions for singular semilinear elliptic boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2000,41(1–2):149–176. 10.1016/S0362-546X(98)00271-5

    Article  MATH  Google Scholar 

  16. Fink AM, Gatica JA, Hernández GE, Waltman P: Approximation of solutions of singular second order boundary value problems. SIAM Journal on Mathematical Analysis 1991,22(2):440–462. 10.1137/0522029

    Article  MathSciNet  MATH  Google Scholar 

  17. Lü H, Bai Z: Positive radial solutions of a singular elliptic equation with sign changing nonlinearities. Applied Mathematics Letters 2006,19(6):555–567. 10.1016/j.aml.2005.08.002

    Article  MathSciNet  MATH  Google Scholar 

  18. Shi J, Yao M: On a singular nonlinear semilinear elliptic problem. Proceedings of the Royal Society of Edinburgh. Section A 1998,128(6):1389–1401. 10.1017/S0308210500027384

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics and Information Science, Zhengzhou University of Light Industry, Zhengzhou, Henan, 450002, China

    Qihu Zhang

Authors
  1. Qihu Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Qihu Zhang.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Reprints and permissions

About this article

Cite this article

Zhang, Q. Existence and Asymptotic Behavior of Positive Solutions to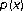-Laplacian Equations with Singular Nonlinearities. J Inequal Appl 2007, 019349 (2007). https://doi.org/10.1155/2007/19349

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1155/2007/19349

Keywords