Generalized Hyers–Ulam stability of ρ-functional inequalities

Abstract

In our research work generalized Hyers-Ulam stability of the following functional inequalities is analyzed by using fixed point approach:

$$\begin{aligned}& \biggl\Vert f(2x+y)+f(2x-y)-2f(x+y)-2f(x-y)-12f(x) \\& \quad {}-\rho \biggl(4f\biggl(x+\frac{y}{2}\biggr)+4\biggl(f\biggl(x- \frac{y}{2}\biggr)-f(x+y)-f(x-y)\biggr)-6f(x),r\biggr) \biggr\Vert \geq \frac{r}{r+\varphi (x, y)} \end{aligned}$$

(0.1)

and

$$\begin{aligned}& \biggl\Vert f(2x+y)+f(2x-y)-4f(x+y)-4f(x-y)-24f(x)+6f(y) \\& \qquad {}-\rho \biggl(8f\biggl(x+\frac{y}{2}\biggr)+8\biggl(f\biggl(x- \frac{y}{2}\biggr)-2f(x+y)-2f(x-y)\biggr)-12f(x)+3f(y),r\biggr) \biggr\Vert \\& \quad \geq \frac{r}{r+\varphi (x, y)} \end{aligned}$$

(0.2)

in the setting of fuzzy matrix, where $\rho \neq 2$ is a real number.

We also discussed Hyers-Ulam stability from the application point of view.

1 Introduction

The abstract characterization of linear spaces of bounded Hilbert space operators in terms of matricially normed spaces [35] implies that quotients, mapping spaces, and different tensor products of operator spaces can be considered operator spaces anew. As a result of this conclusion, the theory of operator spaces is having an increasing impact on operator algebra theory [12].

The proof in [35] made use of the theory of ordered operator spaces [8]. Effros and Ruan [15] demonstrated that the technique of Pisier [32] and Haagerup [21] (as modified in [16]) may be used to provide a purely metric demonstration of this important theorem.

Ulam [45] created the issue of functional equation stability in the year 1940.

Numerous mathematicians later investigated the issue of functional equationś stability. Hyers [22] was the first of them to respond affirmatively to Ulaḿs question in the context of Banach spaces. Aoki [1], Th.M. Rassias [37], Găvruta [18], and many more researchers went on to expand and generalize Hyersś results.

Hyers–Ulam stability investigates the following question: Suppose one has a function that is close to solving an equation; is there an exact solution of the equation that is close to ? The following system can be studied mathematically [22, 26]:

(1.1)

If (1.1) has an exact solution, then it is Ulam–Hyers stable, and if $\forall \epsilon > 0$ there is $\delta >0$ such that if the approximation for solution of (1.1) is , then there is an exact solution of (1.1) that is close to , i.e.,

(1.2)

$\forall t >0$.

This definition is relevant since it implies that if one is investigating a Hyers–Ulam stable system then it does not mean that one has to reach the exact solution (which is usually rather difficult or time consuming). All that is required is to obtain a function that satisfies (1.2). Hyers–Ulam stability ensures that a close exact solution exists.

Cauchy functional equation is

$$ f(\alpha +\beta )=f(\alpha )+f(\beta ), $$

(1.3)

and its solution is known as additive mapping.

Quadratic functional equation is

$$ f(\alpha +\beta )+f(\alpha -\beta )=2f(\alpha )+2f(\beta ), $$

(1.4)

and its solution is known as quadratic mapping.

While discussing the stability, the following techniques are frequently used: extending a function defined on a given set to a solution of the equation in question; determining the form of the solution (which typically satisfies some additional conditions); and using fixed point theorem applications in function spaces. To prove novel fixed point theorems with applications, Rassias and Isac [23] were the first to present applications of the stability theory of functional equations in the year 1996 with the goal of proving applications of fresh fixed point theorems. Stability issues have been thoroughly researched by an array of writers using the fixed point approach; for interesting results concerning this problem, see [10, 17, 23, 25, 31, 33, 38–42].

The Ulam–Hyers stability idea is very important in realistic problems in numerical analysis, biology, and economics. The logistic equation (both differential and difference), the SIS epidemic model, the Cournot model in economics, and the reaction diffusion equation are all generalized to nonlinear systems.

In the year 2022 Pachaiyappan et al. [13] proposed a new method in image security system, they used m-cubic and m-quartic functional equations for encryption and decryption.

To create fuzzy vector topological structure on the space, Katsaras [52] created a fuzzy norm on a vector space. These norms have been defined by certain mathematicians from a variety of angles ([48, 54, 55]). In particular, Bag and Samanta [3] provided an idea of a fuzzy norm in the manner in which Cheng and Mordeson [49] provided a fuzzy metric of the Kramosil and Michalek type [53]. They devised a theorem for how a fuzzy norm can be broken down into a group of crisp norms and looked into some of the characteristics of fuzzy normed spaces [4].

We examine the Hyers-Ulam stability of cubic and quartic ρ-functional inequalities in fuzzy matrix using the notion of fuzzy normed spaces given in [3, 50, 51], and [47].

2 Some fundamental result in fixed point theory

Definition 2.1

[56, 57] Let $\textit{U}\neq \phi$. A function $g: \textit{U} \times \textit{U }\rightarrow [0, \infty ]$ is called a generalized metric on U if g satisfies:

• (1) $g(\alpha , \beta ) = 0$ if and only if $\alpha =\beta$;

• (2) $g(\alpha , \beta ) = g(\beta , \alpha )$ $\forall \alpha , \beta \in \textit{U}$;

• (3) $g(\alpha , \gamma ) \le g(\alpha , \beta ) + g(\beta , \gamma )$ ∀α, β and $\gamma \in \textit{U}$.

Theorem 2.2

[2, 11, 56, 57] Let $V: \textit{U} \rightarrow \textit{U}$ be a strictly contractive mapping with Lipschitz constant $\lambda < 1$. Then, for each $\alpha \in \textit{U}$, either

$$ g\bigl(V^{c} \alpha , V^{c+1} \alpha \bigr) = \infty $$

∀ nonnegative integers c

or ∃ a positive integer $c_{0}$ such that

• (1) $g(V^{c} \alpha , V^{c+1}\alpha ) <\infty$, $\forall c \ge n_{0}$;

• (2) Sequence $\{V^{c} \alpha \}$ converges to the fixed point $\beta ^{*}$ of V;

• (3) $\beta ^{*}$ is the unique fixed point of V in $\beta = \{\beta \in \textit{U }| g(V^{c_{0}} \alpha , \beta ) < \infty \}$;

• (4) $g(\beta , \beta ^{*}) \le \frac{1}{1-\lambda} g(\beta , V\beta )$ $\forall \beta \in \textit{Y}$.

To prove novel fixed point theorems with applications, firstly G. Isac and Th.M. Rassias [24] offered applications of functional equationś stability theory in the year 1996. The stability issues of numerous functional equations have been thoroughly studied by a number of writers using fixed point approach (see [6, 27–29, 34]).

We will notate things as follows:

$N_{m}(U)$ is $n \times n$ matrices in U;

$z_{j}\in N_{1,m}(C)$ means that all other components are zero except j-component that is 1;

$z_{ij}\in N_{m}(C)$ means that all other components are zero except $(i, j)$-component that is 1;

$z_{ij} \otimes \alpha \in N_{m}(C)$ means that all other components are zero except $(i, j)$-component that is α.

For $\alpha \in N_{m}(U)$, $\beta \in N_{m}(U)$,

$$\begin{aligned} \alpha \oplus \beta = \binom{\alpha 0}{0 \beta}. \end{aligned}$$

Let $(U, {\| . \|}_{m})$ be a

matrix normed space:

if and only if $(N_{m}(U), {\| . \|}_{m} )$ is a normed space for each positive integer m and $\| E \alpha D\|_{v} \leq \| E \|\| D \|\| \alpha \|_{m}$ holds for $C\in N_{m}(C)$, $\alpha = [\alpha _{ij}] \in N_{m}(C)$ and $D \in N_{m, v}(C)$);

$(U, {\| . \|}_{m})$ is a

matrix Banach space:

if and only if U is a Banach space and $(U, {\| . \|}_{m})$ is a matrix normed space;

matrix Banach space:

is known as a matrix Banach algebra if U is algebra.

matrix normed space:

is called an $\lambda ^{\infty } - \textit{matrix normed space}$ if $\| \alpha \oplus \beta \|_{m + v} = \max \| \alpha \|_{m}, \| \beta \|_{v}$ holds $\forall \alpha \in N_{m}(U)$, $\beta \in N_{v}(U)$.

Example 2.3

Let $(U, \| . \|)$ be a normed space. Define

$$ \Vert . \Vert _{m}=\frac{ \Vert x \Vert }{1+ \Vert x \Vert };\quad x=[x_{ij}] \in N_{m}(U). $$

Then $(U, \{\|.\|_{m}\})$ is a matrix normed space.

Let us have vector spaces S and W. For $g : S \rightarrow W$ and $m\geq 0$, define $g_{m} : N_{m}(S) \rightarrow N_{m}(W)$ by

$$\begin{aligned} g_{m}\bigl([\alpha _{ij}]\bigr) = \bigl[g(\alpha _{ij})\bigr] \end{aligned}$$

$\forall [\alpha _{ij}] \in N_{m}(S)$.

Lemma 2.4

[56, 57]: Assume that $(U, \|.\|_{m})$ is a matrix normed space

• $\|Z_{vl}\otimes \alpha \|_{m}=\|\alpha \|$ for $\alpha \in U$;

• $\|\alpha _{vl}\|\leq \|[\alpha _{ij}]\|n\leq \sum_{i,j=1}^{n} \|\alpha _{ij}\|$ for $[\alpha _{ij}]\in N_{m}(U)$;

• $\lim_{n\rightarrow \infty }\alpha _{m}=\alpha$ iff $\lim_{n \rightarrow \infty}\alpha _{nij}=\alpha _{ij}$ for $\alpha _{n}=\alpha _{ij}$, $\alpha = [\alpha _{ij}] \in N_{v}(U)$.

We require the definitions and propositions given in [47] to support the primary result.

In Sects. 3 and 4, we solve (0.1) and (0.2) and prove their Hyers-Ulam stability in fuzzy matrix Banach algebra by using the fixed point approach; and in Sect. 5, we discuss Hyers-Ulam stability from the application point of view.

3 Solution of cubic ρ-functional inequality (0.1), a fixed point approach

Throughout the article, U is a matrix normed space with $\|\cdot \|_{n}$, V is matrix Banach algebra with $\|\cdot \|_{n}$, and ρ is a fixed real number with $\rho \neq 2$.

Theorem 3.1

Define a function $\varphi : \textit{U}^{2}\rightarrow [0, \infty )$ such that ∃ $L <1$ resulting in

$$ \sum_{e,f=1}^{n} \varphi (\varrho _{ef}, \sigma _{ef}) \le \sum_{e,f=1}^{n} \frac{1}{8} L \varphi (2\varrho _{ef}, 2\sigma _{ef}) $$

$\forall \varrho =[\varrho _{ef}]$, $\sigma =[\sigma _{ef}] \in M_{n}( \textit{U})$.

Let $p: \textit{U} \rightarrow \textit{V}$ satisfy

$$\begin{aligned}& \bigg\| p_{n}\bigl(2[\varrho _{ef}]+[\sigma _{ef}]\bigr) + p_{n}\bigl(2[\varrho _{ef}]-[ \sigma _{ef}]\bigr) - 2p_{n}\bigl([\varrho _{ef}]+[\sigma _{ef}]\bigr) \\& \qquad{} -2p_{n}\bigl([ \varrho _{ef}]-[\sigma _{ef}]\bigr)-12p_{n}\bigl([\varrho _{ef}]\bigr) \\& \qquad {}-\rho \biggl(4p_{n}\biggl([\varrho _{ef}]+ \frac{[\sigma _{ef}}{2}]\biggr)+4p_{n}\biggl([ \varrho _{ef}]- \frac{[\sigma _{ef}]}{2}\biggr)-p_{n}\bigl([\varrho _{ef}]+[ \sigma _{ef}]\bigr) \\& \qquad {}-p_{n}\bigl([\varrho _{ef}]-[\sigma _{ef}]\bigr)-6p_{n}\bigl([\varrho _{ef}]\bigr),r \biggr) \bigg\| _{n} \\& \quad \geq \sum_{e,f=1}^{n} \frac{r}{r+\varphi ([\varrho _{ef}], [\sigma _{ef}])} \end{aligned}$$

(3.1)

$\forall \varrho =[\varrho _{ef}]$, $\sigma =[\sigma _{ef}] \in M_{n}( \textit{U})$, and $r>0$.

Then $\exists (\varrho ): = N - \lim_{n\to \infty} 8^{n} p ( \frac{\varrho}{2^{n}} )$ for each $\varrho \in M_{n}(\textit{U})$, and a cubic mapping is defined as $A: \textit{U} \rightarrow \textit{V}$ satisfying

$$ \bigl\Vert p_{n}\bigl([\varrho _{ef}]\bigr) - A\bigl([\varrho _{ef}]\bigr) \bigr\Vert _{n} \geq \sum _{e,f=1}^{n} \frac{(16-16L)r}{(16-16L)r+L\varphi (\varrho _{ef}, 0)} $$

(3.2)

$\forall \varrho =[\varrho _{ef}]\in M_{n}(\textit{U})$ and $r>0$.

Proof

Setting $n = 1$ in (3.1) and (3.2), we get

$$\begin{aligned}& \bigg\| p(2\varrho +\sigma )+p(2\varrho -\sigma )-2p(\varrho +\sigma )-2p( \varrho -\sigma )-12p(\varrho ) \\& \qquad {}-\rho (4p\biggl(\varrho +\frac{\sigma}{2}\biggr)+4\biggl(p\biggl(\varrho - \frac{\sigma}{2}\biggr)-p( \varrho +\sigma )-p(\varrho -\sigma )\biggr)-6p \bigl((\varrho ),r\bigr)\bigg\| \\& \quad \geq \frac{r}{r+\varphi (\varrho , \sigma )} \end{aligned}$$

(3.3)

and

$$ \bigl\Vert p(\varrho ) - A(\varrho ) \bigr\Vert \geq \frac{(16-16L)r}{(16-16L)r+L\varphi (\varrho , 0)}. $$

(3.4)

By assuming $p: \textit{U} \rightarrow \textit{V}$ satisfies (3.3).

Set $\varrho = 0$. (3.3) ⇒

$$ \bigl\Vert \bigl(2p(2\varrho ) -16p(\varrho )\bigr),k \bigr\Vert \geq \frac{r}{r+\varphi (\varrho , 0)}, $$

(3.5)

so $\|(p(\varrho )-8p(\frac{\varrho}{2}), \frac{r}{2})\geq \frac{r}{r+\varphi (\frac{\varrho}{2}, 0)}$ $\forall \varrho \in \textit{U}$.

Consider

$$ D = \{j : \textit{U} \rightarrow \textit{V}\}. $$

Proceed with generalized metric on D:

$$ g(j, h) = \inf \biggl\{ \mu \in {\mathbb{R}}_{+} : \bigl\Vert j( \varrho )-h(\varrho ), \mu r \bigr\Vert \geq \frac{r}{r+\varphi (\varrho , 0)}, \forall \varrho \in \textit{U} \text{ and } r> 0\biggr\} , $$

where $\inf \phi = + \infty$. $(D, g)$ is complete (see [46], Lemma 2.1).

Consider the linear mapping $Z: D \rightarrow D$ as

$$ Z g(\varrho ): = 8 g \biggl(\frac{\varrho}{2} \biggr) $$

$\forall \varrho \in \textit{U}$.

Let $j, h \in D$ be given such that $g(j, h)= \epsilon$. Then

$$ \|j(\varrho )-h(\varrho , \epsilon r)\geq \frac{r}{r+\varphi (\varrho , 0)},\quad \forall \varrho \in \textit{U}, \text{and } r> 0. $$

Thus

$$\begin{aligned} \bigl\Vert Zj(\varrho )-Zh(\varrho ), L\epsilon r \bigr\Vert =& \biggl\Vert 8j\biggl(\frac{\varrho}{2}\biggr)-8h\biggl( \frac{\varrho}{2}\biggr), L\epsilon r \biggr\Vert \\ =&\bigg\| j\biggl(\frac{\varrho}{2}\biggr)-h\biggl(\frac{\varrho}{2}, \frac{L}{8}\epsilon r\biggr) \\ \geq& \frac{\frac{Lr}{8}}{\frac{Lr}{8}+\varphi (\frac{\varrho}{2}, 0)} \end{aligned}$$

$\forall \varrho \in \textit{U}$ and all $r >0$. As in Theorem 3.1 [2],

$$ d(Zj, Zh) \le L \epsilon $$

$\forall j, h \in D$.

(3.5) ⇒

$$ \biggl\Vert p(\varrho )-8p\biggl(\frac{\varrho}{2}\biggr), \frac{L}{16}r \biggr\Vert \geq \frac{r}{r+\varphi (\varrho , 0)}, \quad \forall \varrho \in \textit{U} \text{ and } r> 0. $$

So $g(p, Zp)\leq \frac{L}{16}$. Then from Theorem 2.2$\exists A : \textit{U} \rightarrow \textit{V}$ satisfying: (1) K is a fixed point of Z, i.e.,

$$ K \biggl(\frac{\varrho}{2} \biggr) = \frac{1}{8}K(\varrho ) $$

(3.6)

∀ $\varrho \in \textit{U}$. Then K is a unique fixed point of Z in

$$ M=\bigl\{ \iota \in D : g(p, \iota ) < \infty \bigr\} . $$

⇒ K is a unique mapping satisfying (3.6) such that ∃ $\mu \in (0, \infty )$ satisfying

$$ \bigl\Vert p(\varrho )- K(\varrho ), \mu r \bigr\Vert \geq \frac{r}{r+\varphi (\varrho , 0)} $$

$\forall \varrho \in \textit{U}$;

(2) $g(Z^{n} p, K) \rightarrow 0$ as $n \rightarrow \infty$. ⇒

$$ N - \lim_{n\to \infty} 8^{n} p \biggl(\frac{\varrho}{2^{n}} \biggr) = K( \varrho ) $$

$\forall \varrho \in \textit{U}$;

(3) $g(p, K) \le \frac{1}{1-L} g(p, Zp)$, ⇒

$$ g(p, K) \le \frac{L}{16-16L}. $$

So, (3.4) holds.

(3.3) ⇒

$$\begin{aligned}& \|8^{n}\biggl(p\biggl(\frac{2\varrho +\sigma}{2^{n}}\biggr)+p\biggl( \frac{2\varrho -\sigma}{2^{n}}\biggr)-2p\biggl(\frac{\varrho +\sigma}{2^{n}}\biggr)-2p\biggl( \frac{\varrho -\sigma}{2^{n}}\biggr)-12p\biggl(\frac{\varrho}{2^{n}}\biggr)\biggr) \\& \qquad {}-8^{n}\rho \biggl(4p\biggl(\frac{\varrho +\frac{\sigma}{2}}{2^{n}}\biggr)+4p\biggl( \frac{\varrho -\frac{\sigma}{2}}{2^{n}}\biggr)-p\biggl( \frac{\varrho +\sigma}{2^{n}}\biggr)-p\biggl( \frac{\varrho -\sigma}{2^{n}}\biggr)-6p\biggl( \frac{\varrho}{2^{n}}\biggr), 8^{n}r \biggr) \\& \quad \geq \frac{r}{r+\varphi (\frac{\varrho}{2^{n}}, \frac{\sigma}{2^{n}})} \end{aligned}$$

$\forall \varrho , \sigma \in \textit{U}$, $r>0$, and $n \in \textit{N}$

$$\begin{aligned}& \|8^{n}\biggl(p\biggl(\frac{2\varrho +\sigma}{2^{n}}\biggr)+p\biggl( \frac{2\varrho -\varrho}{2^{n}}\biggr)-2p\biggl(\frac{\varrho +\sigma}{2^{n}}\biggr)-2p\biggl( \frac{\varrho -\sigma}{2^{n}}\biggr)-12p\biggl(\frac{\varrho}{2^{n}}\biggr)\biggr) \\& \qquad {}-8^{n}\rho \biggl(4p\biggl(\frac{\varrho +\frac{\sigma}{2}}{2^{n}}\biggr)+4p\biggl( \frac{\varrho -\frac{\sigma}{2}}{2^{n}}\biggr)-p\biggl( \frac{\varrho +\sigma}{2^{n}}\biggr)-p\biggl( \frac{\varrho -\sigma}{2^{n}}\biggr)-6p\biggl( \frac{\varrho}{2^{n}}\biggr), r\biggr) \\& \quad \geq \frac{\frac{1}{8^{n}}}{\frac{1}{8^{n}}+\frac{L^{n}}{8^{n}}\varphi (\varrho , \sigma )}. \end{aligned}$$

Since $\lim_{n\rightarrow \infty} \frac{\frac{1}{8^{n}}}{\frac{1}{8^{n}}+\frac{L^{n}}{8^{n}}\varphi (\varrho , \sigma )} =1$ ∀ $\varrho , \sigma \in \textit{U}$ and $r>0$.

$$\begin{aligned}& \bigl\Vert K(2\varrho +\sigma )+K(2\varrho -\sigma )-2K(\varrho +\sigma )-2K( \varrho -\sigma )-12K(\varrho ) \bigr\Vert \\& \quad = \biggl\Vert \rho \biggl(4K\biggl(\varrho +\frac{\sigma}{2}\biggr)+4K \biggl(\varrho -\frac{\sigma}{2}\biggr)-K( \varrho +\sigma )-K(\varrho -\sigma )-6K(\varrho )\biggr) \biggr\Vert \end{aligned}$$

$\forall \varrho , \sigma \in \textit{U}$. By Lemma 2.1 of [47], $K: \textit{U}\rightarrow \textit{V}$ is cubic. □

Example 3.2

Let $\psi : \mathbb{R}^{2}\rightarrow [0, \infty )$ be defined by

$$ \psi (x)=\textstyle\begin{cases} 0, & \text{if }x=0; \\ \zeta x^{3}, & \text{if } \vert x \vert < 1; \\ \zeta , & \text{otherwise}, \end{cases} $$

where $\zeta >0$ is a constant. Define a function $h_{m}:\mathbb{R}\rightarrow \mathbb{R}$ by

$$ h_{m}(x)=\sum^{\infty}_{n=0} \frac{\psi (2^{n}x)}{8}. $$

Then $h_{m}$ satisfies functional inequality (3.2).

Let

$$\begin{aligned}& p_{m}(x) = h_{m}(x)+h_{m}(-x), \\& p_{m}(x) = \zeta x^{3}, \\& p_{m}\biggl(\frac{x}{2}\biggr) = \frac{\zeta x^{3} }{2^{3}} \end{aligned}$$

$\forall x \in \mathbb{R}$. We define the set $S = \{p_{m}:\mathbb{R}\rightarrow \mathbb{R}, p_{m}(0) = 0\}$ and consider the generalized metric on S as described in the proof of the above theorem. Also consider the mapping $j: S\rightarrow S$ such that

$$ Jp_{m}(x)=8p\biggl(\frac{x}{2}\biggr)=p(x). $$

Now

$$\begin{aligned} \lim_{c\rightarrow \infty}8^{c}p\biggl(\frac{x}{2} \biggr) =& \lim_{c \rightarrow \infty}8^{c}\biggl(\frac{\zeta x^{3}}{2^{3}} \biggr) \\ =& \lim_{c\rightarrow \infty}8^{c}\biggl( \frac{\zeta x^{3}}{2^{3(1-c)}}\biggr) \\ =& K(x). \end{aligned}$$

It is clear that

$$ K\biggl(\frac{x}{2}\biggr)=\frac{1}{8}K(x). $$

Moreover, we have

$$\begin{aligned} \biggl\Vert p(x)-8p\biggl(\frac{x}{2}\biggr) \biggr\Vert =& \biggl\Vert \zeta x^{3}-8 \frac{\zeta x^{3}}{2^{3}} \biggr\Vert \\ \leq & \psi \biggl(\frac{x}{2}, 0\biggr)+ \psi \biggl(- \frac{x}{2}, 0\biggr) \\ \leq & \frac{L}{16}\bigl( \psi (x, 0)+\psi (-x, 0)\bigr). \end{aligned}$$

Hence

$$ d(p, Lp)\leq \frac{L}{16}. $$

We can also show that

$$ d(p, K)\leq \frac{1}{1-L}d(p, Jp). $$

The above result implies the following:

$$ d(p, K)\leq \frac{16}{16-16L}. $$

Therefore all the conditions are fulfilled, and by Lemma 2.4, $K:\mathbb{R}\rightarrow \mathbb{R}$ satisfies (3.2).

Corollary 3.3

Assume that a real number $\rho > 3$, $\theta \geq 0$ and $p: \textit{U}\rightarrow \textit{V}$ satisfies

$$\begin{aligned}& \bigg\| p\bigl(2[\varrho _{ef}]+[\sigma _{ef}] \bigr)+p\bigl(2[\varrho _{ef}]-[\sigma _{ef}]\bigr)-2p\bigl([ \varrho _{ef}]+[\sigma _{ef}]\bigr) \\& \qquad {}-2p\bigl([\varrho _{ef}]-[\sigma _{ef}]\bigr)-12p\bigl([ \varrho _{ef}]\bigr) \\& \qquad {}-\rho \biggl(4p\biggl([\varrho _{ef}]+\frac{[\sigma _{ef}]}{2}\biggr) \\& \qquad {}+4 \biggl(p\biggl([\varrho _{ef}- \frac{[\sigma _{ef}]}{2}\biggr)-p\bigl([\varrho _{ef}]+[\sigma _{ef}]\bigr)-p\bigl([ \varrho _{ef}]-[\sigma _{ef}]\bigr)\biggr)-6p\bigl([\varrho _{ef}]\bigr), r\biggr)\bigg\| _{n} \\& \quad \geq \sum_{e,f=1}^{n} \frac{r}{r+\theta ( \Vert [\varrho _{ef}] \Vert ^{w}+ \Vert [\sigma _{ef}] \Vert ^{w})} \end{aligned}$$

(3.7)

$\forall \varrho =[\varrho _{ef}]$, $\sigma =[\sigma _{ef}] \in M_{n}( \textit{U})$ and $r>0$. Then $p(\varrho ): = N- \lim_{n\rightarrow \infty}8^{n}p( \frac{\varrho}{2^{n}})$ exists for each $\varrho =[\varrho _{ef}] \in M_{n}(\textit{U})$ and defines a cubic mapping $A: \textit{U}\rightarrow \textit{V}$ satisfying

$$ \bigl\Vert \bigl(p\bigl([\varrho _{ef}]\bigr)-A\bigl([\varrho _{ef}]\bigr), r\bigr) \bigr\Vert _{n}\geq \frac{2(2^{w}-8)r}{2(2^{w}-8)r+\sum_{e,f=1}^{n}\theta \Vert [\varrho _{ef}] \Vert ^{w}} $$

$\forall \varrho =[\varrho _{ef}] \in M_{n}(\textit{U})$ and $r>0$.

Proof

Theorem 3.1 leads to the proof by choosing $\sum_{e,f=1}^{n}\phi (\varrho _{ef}, \sigma _{ef}): = \sum_{e,f=1}^{n} \theta (\|[\varrho _{ef}]\|^{w}+\|[\sigma _{ef}]\|^{w})$ $\forall \varrho =[\varrho _{ef}]$, $\sigma =[\sigma _{ef}] \in M_{n}( \textit{U})$. Then we can set $L=2^{3-w}$ to get the desired result. □

Theorem 3.4

Let $\varphi : \textit{U}^{2} \rightarrow [0, \infty )$ and ∃ $L <1$ resulting in

$$ \sum_{e,f=1}^{n} \varphi \bigl([\varrho _{ef}], [\sigma _{ef}]\bigr) \le \sum _{e,f=1}^{n} 8 L \varphi \biggl(\frac{[\varrho _{ef}]}{2}, \frac{[\sigma _{ef}]}{2}\biggr) $$

$\forall \varrho =[\varrho _{ef}]$, $\sigma =[\sigma _{ef}] \in M_{n}( \textit{U})$.

Assume a mapping $p: \textit{U} \rightarrow \textit{V}$ such that

$$\begin{aligned}& \biggl\Vert p_{n}\bigl(2[\varrho _{ef}]+ [ \sigma _{ef}]\bigr) + p_{n}\bigl(2[\varrho _{ef}]-[ \sigma _{ef}]\bigr) - 2p_{n}\bigl([\varrho _{ef}]+[ \sigma _{ef}]\bigr) \\& \qquad {}-2p_{n}\bigl([ \varrho _{ef}]-[ \sigma _{ef}]\bigr)-12p_{n}\bigl([\varrho _{ef}] \bigr) \\& \qquad {}-\rho \biggl(4p_{n}\biggl([\varrho _{ef}]+ \frac{[\sigma _{ef}]}{2}\biggr)+4p_{n}\biggl([ \varrho _{ef}]- \frac{[\sigma _{ef}]}{2}\biggr) \\& \qquad {}-p_{n}\bigl([\varrho _{ef}]+[ \sigma _{ef}]\bigr)-p_{n}\bigl([\varrho _{ef}]-[\sigma _{ef}]\bigr)-6p_{n}\bigl([\varrho _{ef}]\bigr),r \biggr) \biggr\Vert _{n} \\& \quad \geq \sum_{e,f=1}^{n} \frac{r}{r+\varphi ([\varrho _{ef}], [\sigma _{ef}])} \end{aligned}$$

(3.8)

$\forall \varrho =[\varrho _{ef}]$, $\sigma =[\sigma _{ef}] \in M_{n}( \textit{U})$ and $r>0$.

Then $\exists (\varrho ): = N - \lim_{n\to \infty} \frac{1}{8^{n}} p(2_{n} \varrho )$ for each $\varrho \in M_{n}(\textit{U})$, and it defines the cubic mapping $A: \textit{U} \rightarrow \textit{V}$ satisfying

$$ \bigl\Vert p_{n}\bigl([\varrho _{ef}]\bigr) - A\bigl([\varrho _{ef}]\bigr) \bigr\Vert _{n} \geq \sum _{e,f=1}^{n} \frac{(16-16L)r}{(16-16L)r+L\varphi ([\varrho _{ef}], 0)} $$

(3.9)

$\forall \varrho =[\varrho _{ef}]\in M_{n}(\textit{U})$ and $r>0$.

Proof

From the proof of Theorem 3.1, $(D, g)$ is a generalized metric space.

(3.5) ⇒

$$ \biggl\Vert p(\varrho )-\frac{1}{8}p(2\varrho ), \frac{1}{16}r \biggr\Vert \geq \frac{r}{r+\varphi (\varrho , 0)} $$

$\forall \varrho =[\varrho _{ef}]\in M_{n}(\textit{U})$ and $r>0$. Consider the linear mapping $Z: D\rightarrow D$ satisfying

$$ Zj(\varrho ):=\frac{1}{8}j(2\varrho ) $$

$\forall \varrho =[\varrho _{ef}] \in M_{n}(\textit{U})$. Then $g(p, Zp)\leq \frac{1}{16}$. Hence

$$ g(p, C)\leq \frac{1}{16-16L}. $$

So, (3.9) holds.

The rest is comparable to the proof of Theorem 3.1. □

Corollary 3.5

Assume that a real number with $0 < p < 3$, $\theta \geq 0$ and $p: \textit{U}\rightarrow \textit{V}$ satisfies (3.7). Then $\exists (\varrho ): = N- \lim_{n\rightarrow \infty} \frac{1}{8^{n}}p(2^{n}\varrho )$ for each $\varrho =[\varrho _{ef}] \in M_{n}(\textit{U})$, and it defines a cubic mapping $A: \textit{U}\rightarrow \textit{V}$ satisfying

$$ \bigl\Vert \bigl(p\bigl([\varrho _{ef}]\bigr)-A\bigl([\varrho _{ef}]\bigr), r\bigr) \bigr\Vert _{n}\geq \frac{2(8-2^{w})r}{2(8-2^{w})r+ \sum_{e,f=1}^{n} \theta \Vert [\varrho _{ef}] \Vert ^{w}} $$

$\forall \varrho =[\varrho _{ef}] \in M_{n}(\varrho )$ and $r>0$.

Proof

The proof follows from Theorem 3.4 by taking $\sum_{e,f=1}^{n}\phi ([\varrho _{ef}], [\sigma _{ef}]): = \sum_{e,f=1}^{n} \theta (\|[\varrho _{ef}]\|^{w}+\|[\sigma _{ef}]\|^{w})$ $\forall \varrho =[\varrho _{ef}]$, $\sigma =[\sigma _{ef}] \in M_{n}( \textit{U})$. Then we can choose $L=2^{w-3}$, and we get the desired result. □

4 Solution of quartic ρ-functional inequality (0.2), a fixed point approach

Theorem 4.1

Assume that a function $\varphi : U^{2} \rightarrow [0, \infty )$ s.t. ∃ $L <1$ resulting in

$$ \sum_{e,f=1}^{n} \varphi \bigl([\varrho _{ef}], [\sigma _{ef}]\bigr) \le \sum _{i,j=1}^{n} \frac{1}{16} L \varphi \bigl(2[x_{ij}], 2[y_{ij}]\bigr) $$

$\forall \varrho =[\varrho _{ef}]$, $\sigma =[\sigma _{ef}] \in M_{n}( \textit{U})$.

Let $p: \textit{U} \rightarrow \textit{V}$ satisfy $p(0)=0$ and

$$\begin{aligned}& \biggl\Vert p_{n}\bigl(2[\varrho _{ef}]+[ \sigma _{ef}]\bigr) + p_{n}\bigl(2[\varrho _{ef}]-[ \sigma _{ef}]\bigr) - 4p_{n}\bigl([\varrho _{ef}]+[ \sigma _{ef}]\bigr)-4p_{n}\bigl([ \varrho _{ef}]-[ \sigma _{ef}]\bigr) \\& \qquad {}-24p_{n}\bigl([\varrho _{ef}] \bigr)+6p_{n}\bigl([ \sigma _{ef}]\bigr) \\& \qquad {}-\rho \biggl(8p_{n}\biggl([\varrho _{ef}]+ \frac{[\sigma _{ef}]}{2}\biggr)+8p_{n}\biggl([ \varrho _{ef}]- \frac{[\sigma _{ef}]}{2}\biggr)-2p_{n}\bigl([\varrho _{ef}]+[ \sigma _{ef}]\bigr) \\& \qquad {}-2p_{n}\bigl([\varrho _{ef}]-[\sigma _{ef}]\bigr)-12p_{n}\bigl([ \varrho _{ef}] \bigr)+3p_{n}\bigl([\sigma _{ef}]\bigr),r\biggr) \biggr\Vert _{n} \\& \quad \geq \sum_{e,f=1}^{n} \frac{r}{r+\varphi ([\varrho _{ef}], [\sigma _{ef}])} \end{aligned}$$

(4.1)

$\forall \varrho =[\varrho _{ef}]$, $\sigma =[\sigma _{ef}] \in M_{n}( \textit{U})$ and $r>0$.

Then $\exists B(x): = N - \lim_{n\to \infty} 16^{n} p ( \frac{\varrho}{2^{n}} )$ for each $\varrho \in M_{n}(\textit{U})$, and it defines a quartic mapping $B: \textit{U} \rightarrow \textit{V}$ satisfying

$$ \bigl\Vert p_{n}\bigl([\varrho _{ef}]\bigr) - B\bigl([\varrho _{ef}]\bigr) \bigr\Vert _{n} \geq \sum _{e,f=1}^{n} \frac{(32-32L)r}{(32-32L)r+L\varphi ([\varrho _{ef}], 0)} $$

(4.2)

$\forall \varrho =[\varrho _{ef}]\in M_{n}(\textit{U})$ and $r>0$.

Proof

Set $n = 1$ in (4.1) and (4.2), we get

$$\begin{aligned}& \biggl\Vert p(2\varrho +\sigma )+p(2\varrho -\sigma )-4p( \varrho +\sigma )-4p( \varrho -\sigma )-24p(\varrho )+6p(\sigma ) \\& \qquad {}-\rho \biggl(8p\biggl(\varrho +\frac{\sigma}{2}\biggr)+8\biggl(p\biggl( \varrho -\frac{\sigma}{2}\biggr)-2p( \varrho +\sigma )-2p(\varrho -\sigma ) \biggr) \\& \qquad {}-12p(\varrho )+3p(\sigma ),r\biggr) \biggr\Vert \\& \quad \geq \frac{r}{r+\varphi (\varrho , \sigma )} \end{aligned}$$

(4.3)

and

$$ \bigl\Vert p(\varrho ) - B(\varrho ) \bigr\Vert \geq \frac{(16-16L)r}{(16-16L)r+L\varphi (\varrho , 0)} $$

(4.4)

$\forall \varrho =[\varrho _{ef}]\in M_{n}(\textit{U})$ and $r>0$.

When $\sigma =0$, (4.3) ⇒

$$ \bigl\Vert 2p(2\varrho )-32p(\varrho ), r \bigr\Vert = \bigl\Vert 32p(\varrho )-2p(2\varrho ), r \bigr\Vert \geq \frac{r}{r+\varphi (\varrho , 0)} $$

(4.5)

$\forall \varrho \in \textit{U}$.

By considering the linear mapping $Z: D\rightarrow D$ that satisfies

$$ Z j(\varrho ): = 16 j \biggl(\frac{\varrho}{2} \biggr) $$

$\forall \varrho \in \textit{U}$.

Let $j, h \in D$ be given such that $g(j, h)= \epsilon$. Then

$$ \|j(\varrho )-h(\varrho , \epsilon r)\geq \frac{r}{r+\varphi (\varrho , 0)}, \quad \forall \varrho \in \textit{U}, \text{and } r> 0. $$

Hence

$$\begin{aligned} \bigl\Vert Zj(\varrho )-Zh(\varrho ), L\epsilon r \bigr\Vert =& \biggl\Vert 16j\biggl(\frac{\varrho}{2}\biggr)-16h\biggl( \frac{\varrho}{2}\biggr), L \epsilon r \biggr\Vert \\ =&\|j\biggl(\frac{\varrho}{2}\biggr)-h\biggl(\frac{\varrho}{2}, \frac{L}{16}\epsilon r\biggr) \\ \geq& \frac{\frac{Lr}{16}}{\frac{Lr}{16}+\varphi (\frac{\varrho}{2}, 0)} \geq \frac{\frac{Lr}{16}}{\frac{Lr}{16}+\varphi (\varrho , 0)}= \frac{r}{r+\varphi (\varrho , 0)} \end{aligned}$$

$\forall \varrho \in \textit{U}$ and $r >0$. So $g(p, Zp)\leq \frac{L}{32}$. Following from the evidence of Theorem 2.2, ∃ $B: \textit{U}\rightarrow \textit{V}$ satisfying:

(1) B is a fixed point of Z, i.e.,

$$ B \biggl(\frac{\varrho}{2} \biggr) = \frac{1}{16}B(\varrho ) $$

(4.6)

$\forall \varrho \in \textit{U}$. Then B is the unique fixed point of Z in

$$ M=\bigl\{ j\in D : g(p, j) < \infty \bigr\} . $$

⇒ B is the unique mapping satisfying (4.6) such that ∃ $\mu \in (0, \infty )$ satisfying

$$ \bigl\Vert p(\varrho )- B(\varrho ), \mu r \bigr\Vert \geq \frac{r}{r+\varphi (\varrho , 0)} $$

$\forall \varrho \in \textit{U}$;

(2) $g(Z^{n} p, B) \rightarrow 0$ as $n \rightarrow \infty$.

⇒

$$ N - \lim_{n\to \infty} 16^{n} p \biggl(\frac{\varrho}{2^{n}} \biggr) = B(\varrho ) $$

∀ $\varrho \in \textit{U}$;

(3) $g(p, B) \le \frac{1}{1-L} g(p, Zp)$.

⇒

$$ g(p, B) \le \frac{L}{32-32L}. $$

So, (4.2) holds.

By utilizing the same technique of Theorem 3.1 and (4.3) ⇒

$$\begin{aligned}& \bigl\Vert B(2\varrho +\sigma )+B(2\varrho -\sigma )-4B(\varrho +\sigma )-4B( \varrho -\sigma )-24B(\varrho )+6B(\sigma ) \bigr\Vert \\& \quad = \biggl\Vert \rho \biggl(8B\biggl(\varrho +\frac{\sigma}{2}\biggr)+8B \biggl(\varrho -\frac{\sigma}{2}\biggr)-2B( \varrho +\sigma )-2B(\varrho -\sigma )\biggr)-12B(\varrho )+3B(\sigma ) \biggr\Vert \end{aligned}$$

$\forall \varrho , \sigma \in \textit{U}$. So, $B: \textit{U}\rightarrow \textit{V}$ is quartic by Lemma 3.1 of [47]. □

Example 4.2

Let $\psi : \mathbb{R}^{2}\rightarrow [0, \infty )$ be defined by

$$ \psi (x)=\textstyle\begin{cases} 0, & \text{if }x=0; \\ \zeta x^{4}, & \text{if } \vert x \vert < 1; \\ \zeta , & \text{otherwise}, \end{cases} $$

where $\zeta >0$ is a constant. Define a function $h_{m}:\mathbb{R}\rightarrow \mathbb{R}$ by

$$ h_{m}(x)=\sum^{\infty}_{n=0} \frac{\psi (2^{n}x)}{16}. $$

Then $h_{m}$ satisfies functional inequality (4.2).

By the same steps as in Example 3.2, we can find a mapping satisfying inequality (4.2).

Corollary 4.3

Assume that a real number with $\rho > 4$, $\theta \geq 0$ and $p: \textit{U}\rightarrow \textit{V}$ satisfies $p(0)=0$ and

$$\begin{aligned}& \biggl\Vert p\bigl(2[\varrho _{ef}]+[\sigma _{ef}]\bigr)+p\bigl(2[\varrho _{ef}]-[\sigma _{ef}] \bigr)-4p\bigl([ \varrho _{ef}]+[\sigma _{ef}]\bigr) \\& \qquad {}-4p\bigl([ \varrho _{ef}]-[\sigma _{ef}]\bigr)-24p\bigl([ \varrho _{ef}]\bigr)+6p\bigl([\sigma _{ef}]\bigr) \\& \qquad {}-\rho \biggl(8p\biggl([\varrho _{ef}]+\frac{[\sigma _{ef}]}{2}\biggr) \\& \qquad {}+8 \biggl(p\biggl([\varrho _{ef}]- \frac{[\sigma _{ef}]}{2}\biggr)-2p\bigl([ \varrho _{ef}]+[\sigma _{ef}]\bigr)-2p\bigl([ \varrho _{ef}]-[\sigma _{ef}]\bigr)\biggr) \\& \qquad {}-12p\bigl([\varrho _{ef}]\bigr)+3p\bigl([\sigma _{ef}]\bigr), r\biggr) \biggr\Vert _{n} \\& \quad \geq \sum_{e,f=1}^{n} \frac{r}{r+\theta ( \Vert [\varrho _{ef}] \Vert ^{w}+ \Vert [\sigma _{ef}] \Vert ^{w})} \end{aligned}$$

(4.7)

$\forall \varrho =[\varrho _{ef}]$, $\sigma =[\sigma _{ef}] \in M_{n}( \textit{U})$ and $r>0$. Then $p(\varrho ): = N- \lim_{n\rightarrow \infty}16^{n}p( \frac{\varrho}{2^{n}})$ exists for each $\varrho =[\varrho _{ef}] \in M_{n}(\textit{U})$ and defines a quartic mapping $B: \textit{U}\rightarrow \textit{V}$ satisfying

$$ \bigl\Vert \bigl(p\bigl([\varrho _{ef}]\bigr)-B\bigl([\varrho _{ef}]\bigr), r\bigr) \bigr\Vert _{n}\geq \frac{2(2^{w}-16)r}{2(2^{w}-16)r+\sum_{e, f=1}^{n}\theta \Vert [\varrho _{ef}] \Vert ^{w}} $$

$\forall \varrho =[\varrho _{ef}] \in M_{n}(\textit{U})$ and $r>0$.

Proof

The proof follows from Theorem 4.1 by choosing $\sum_{e, f=1}^{n}\phi ([\varrho _{ef}], [\sigma _{ef}]): = \sum_{e, f=1}^{n}\theta (\|[\varrho _{ef}]\|^{w}+\|[\sigma _{ef}]\|^{w})$ $\forall \varrho =[\varrho _{ef}]$, $\sigma =[\sigma _{ef}] \in M_{n}( \textit{U})$. Then we can choose $L=2^{4-w}$ for the desired result. □

Theorem 4.4

Assume a function $\varphi : U^{2} \rightarrow [0, \infty )$ such that ∃ $L <1$ resulting in

$$ \sum_{e,f=1}^{n} \varphi \bigl([\varrho _{ef}], [\sigma _{ef}]\bigr) \le \sum _{e,f=1}^{n} 16 L \varphi \biggl(\frac{[\varrho _{ef}]}{2}, \frac{[\sigma _{ef}]}{2}\biggr) $$

$\forall \varrho =[x_{ef}]$, $\sigma =[\sigma _{ef}] \in M_{n}( \textit{U})$.

Let $p: \textit{U} \rightarrow \textit{V}$ satisfy $p(0)=0$ and

$$\begin{aligned}& \bigg\| p_{n}\bigl(2[\varrho _{ef}]+[\sigma _{ef}]\bigr) + p_{n}\bigl(2[\varrho _{ef}]-[ \sigma _{ef}]\bigr) - 4p_{n}\bigl([\varrho _{ef}]+[\sigma _{ef}]\bigr) \\& \qquad {}-4p_{n}\bigl([ \varrho _{ef}]-[\sigma _{ef}]\bigr)-24p_{n}\bigl([\varrho _{ef}] \bigr)+6p_{n}\bigl([ \sigma _{ef}]\bigr) \\& \qquad {}-\rho \biggl(8p_{n}\biggl([\varrho _{ef}]+ \frac{[\sigma _{ef}]}{2}\biggr)+8p_{n}\biggl([ \varrho _{ef}]- \frac{[\sigma _{ef}]}{2}\biggr)-2p_{n}\bigl(\varrho _{ef}]+[ \sigma _{ef}]\bigr) \\& \qquad {}-2p_{n}\bigl([\varrho _{ef}]-[\sigma _{ef}]\bigr)-12p_{n}\bigl([ \varrho _{ef}] \bigr)+3p_{n}\bigl([\sigma _{ef}]\bigr),r\biggr) \bigg\| _{n} \\& \quad \geq \sum_{e,f=1}^{n} \frac{r}{r+\varphi ([\varrho _{ef}], [\sigma _{ef}])} \end{aligned}$$

(4.8)

$\forall \varrho =[\varrho _{ef}]$, $\sigma =[\sigma _{ef}] \in M_{n}( \textit{U})$ and $r>0$.

Then $\exists B(\varrho ): = N - \lim_{n\to \infty} \frac{1}{16^{n}} p(2_{n} \varrho )$ for each $\varrho \in M_{n}(\textit{U})$, and it defines a quartic mapping $B: \textit{U} \rightarrow \textit{V}$ satisfying

$$ \bigl\Vert p_{n}\bigl([\varrho _{ef}]\bigr) - B\bigl([\varrho _{ef}]\bigr) \bigr\Vert _{n} \geq \sum _{e,f=1}^{n} \frac{(32-32L)r}{(32-32L)r+L\varphi ([\varrho _{ef}], 0)} $$

(4.9)

$\forall \varrho =[\varrho _{ef}]\in M_{n}(\textit{U})$ and $r>0$.

Proof

From Theorem 3.1$(D, g)$ is a generalized metric space

(4.5) ⇒

$$ \biggl\Vert p(\varrho )-\frac{1}{16}p(2\varrho ), \frac{1}{32}r \biggr\Vert \geq \frac{r}{r+\varphi (\varrho , 0)} $$

$\forall \varrho =[\varrho _{ef}]\in M_{n}(\textit{U})$ and $r>0$. A linear mapping $Z: D\rightarrow D$ satisfies

$$ Zj(\varrho ):=\frac{1}{16}j(2\varrho ) $$

$\forall \varrho =[\varrho _{ef}] \in M_{n}(\textit{U})$. Then $g(p, Zp)\leq \frac{1}{32}$. Hence

$$ g(p, B)\leq \frac{1}{32-32L}. $$

So, (4.9) holds.

The remainder of the proof is similar to Theorem 4.1. □

Corollary 4.5

Assume that a real number with $0 < \rho < 4$, $\theta \geq 0$ and $p: \textit{U}\rightarrow \textit{V}$ is a mapping satisfying $p(0)=0$ and (4.7). Then $\exists B(\varrho ): = N- \lim_{n\rightarrow \infty} \frac{1}{16^{n}}p(2^{n}\varrho )$ for each $\varrho =[\varrho _{ef}] \in M_{n}(\textit{U})$ and defines a quartic mapping $B: \textit{U}\rightarrow \textit{V}$ satisfying

$$ \bigl\Vert \bigl(p\bigl([\varrho _{ef}]\bigr)-B\bigl([\varrho _{ef}]\bigr), r\bigr) \bigr\Vert _{n}\geq \frac{2(16-2^{w})r}{2(16-2^{w})r+ \sum_{e,f=1}^{n} \theta \Vert [\varrho _{ef}] \Vert ^{w}} $$

$\forall \varrho =[\varrho _{ef}] \in M_{n}(\textit{U})$ and all $r>0$.

Proof

The proof follows from Theorem 4.4 by choosing $\sum_{e,f=1}^{n}\phi ([\varrho _{ef}], [\sigma _{ef}]): = \sum_{e,f=1}^{n} \theta (\|[\varrho _{ef}]\|^{w}+\|[\sigma _{ef}]\|^{w})$ ∀ $\varrho =[\varrho _{ef}]$, $\sigma =[\sigma _{ef}] \in M_{n}( \textit{U})$. Then we can choose $L=2^{w-4}$ for the desired result. □

5 Application

The Hyers-Ulam stability idea is very useful in practical applications in numerical analysis, biology, and economics. The SIS epidemic model, logistic equation (both difference and differential), a response diffusion equation, and Cournot model in economics are all generalized to nonlinear systems.

Local Hyers-Ulam stability for nonlinear differential and difference equations will be investigated using a concept similar to local Lyapunov stability. For this, consider systems (1.1), (1.2), and suppose

(5.1)

also suppose that is small, so linearize in it. By substituting (1.1) and (1.2), one obtains

(5.2)

Thus one has the following.

Proposition 5.1

If there is a constant $\mathfrak{A}$ such that system (1.1) is locally Hyers-Ulam stable, then

(5.3)

Now consider a discrete system similarly

(5.4)

by supposing again

(5.5)

assume that is small, so linearize in it. We obtain the following.

Proposition 5.2

A sufficient condition for system (5.4) to be locally Hyers-Ulam stable is that there is constant $\mathfrak{A}$ such that

(5.6)

Now we are going to discuss some applications of Hyers-Ulam stability.

1: Logistic differential equation:

(5.7)

Proposition 5.1 states that system (5.6) is locally Hyers–Ulam stable if there is a constant $\mathfrak{A}$ such that

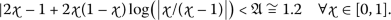(5.8)

2: Logistic difference equation:

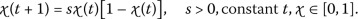(5.9)

By applying (5.6), system (5.9) is locally Hyers-Ulam stable if there is a constant $\mathfrak{A}$ such that

$$ 0< s< \mathfrak{A}< 1. $$

3: SIS infection model in constant population:

The system is given by the equations

$$\begin{aligned}& \frac{d\mathcal{R}}{dt} = -c\mathcal{RL}, \\& \frac{d\mathcal{R}}{dt} = -c\mathcal{RL}-z\mathcal{L}, \end{aligned}$$

(5.10)

where $\mathcal{N}$ (population size) is divided into $\mathcal{R}(t)$ and $\mathcal{L}(t)$ (susceptible and infectious individuals, respectively).

Hence, $\mathcal{N}=\mathcal{R}+\mathcal{L}$, $c, z > 0$.

By rescaling $\mathcal{N}$, we obtain (5.7), thus system (5.10) is locally Hyers-Ulam stable. This is significant since determining the true number of infections can be quite challenging. Stochastic effects can also be substantial. Thus, if deterministic model is close enough to reality, its convergence to an exact solution is guaranteed by the local Hyers–Ulam stability.

6 Conclusion

In this research article, we have proved generalized Hyers-Ulam stability of cubic and quartic ρ-functional inequalities in fuzzy matrix by using the fixed point approach, where $\rho \neq 2$ is a real number. We also provided examples to support our results. Finally, we discussed Hyers-Ulam stability from the application point of view.