- Research Article
- Open access
- Published:
Approximate solutions of the generalized Gołąb-Schinzel equation
Journal of Inequalities and Applications volume 2006, Article number: 89402 (2006)
Abstract
Motivated by the problem of R. Ger, we show that the generalized Gołąb-Schinzel equation is superstable in the class of functions hemicontinuous at the origin. As a consequence, we obtain the form of approximate solutions of that equation.
References
Aczél J, Dhombres J: Functional Equations in Several Variables, Encyclopedia of Mathematics and Its Applications. Volume 31. Cambridge University Press, Cambridge; 1989:xiv+462.
Brillouët-Belluot N: On some functional equations of Gołąb-Schinzel type. Aequationes Mathematicae 1991,42(2–3):239–270.
Brillouët-Belluot N, Dhombres J: Équations fonctionnelles et recherche de sous-groupes. Aequationes Mathematicae 1986,31(2–3):253–293.
Brzdęk J: Subgroups of the group
 and a generalization of the Gołąb-Schinzel functional equation. Aequationes Mathematicae 1992,43(1):59–71. 10.1007/BF01840475
and a generalization of the Gołąb-Schinzel functional equation. Aequationes Mathematicae 1992,43(1):59–71. 10.1007/BF01840475Brzdęk J: Some remarks on solutions of the functional equation
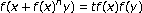 . Publicationes Mathematicae Debrecen 1993,43(1–2):147–160.
. Publicationes Mathematicae Debrecen 1993,43(1–2):147–160.Brzdęk J: The Gołąb-Schinzel equation and its generalizations. Aequationes Mathematicae 2005,70(1–2):14–24. 10.1007/s00010-005-2781-y
Chudziak J: Approximate solutions of the Gołąb-Schinzel equation. Journal of Approximation Theory 2005,136(1):21–25. 10.1016/j.jat.2005.04.011
Chudziak J: On a functional inequality related to the stability problem for the Gołąb-Schinzel equation. Publicationes Mathematicae Debrecen 2005,67(1–2):199–208.
Chudziak J: Stability of the generalized Gołąb-Schinzel equation. Acta Mathematica Hungarica 2006, 113: 115–126.
Chudziak J, Tabor J: On the stability of the Gołąb-Schinzel functional equation. Journal of Mathematical Analysis and Applications 2005,302(1):196–200. 10.1016/j.jmaa.2004.07.053
Forti GL: Hyers-Ulam stability of functional equations in several variables. Aequationes Mathematicae 1995,50(1–2):143–190. 10.1007/BF01831117
Ger R: A collection of problems in stability theory. Report of Meeting, the 38th International Symposium on Functional Equations, June 2000, Noszvaj Aequationes Mathematicae 61 (2001), no. 3, 281–320 Aequationes Mathematicae 61 (2001), no. 3, 281–320
Gudder S, Strawther D: Orthogonally additive and orthogonally increasing functions on vector spaces. Pacific Journal of Mathematics 1975,58(2):427–436.
Hyers DH, Isac G, Rassias ThM: Stability of Functional Equations in Several Variables, Progress in Nonlinear Differential Equations and Their Applications. Volume 34. Birkhäuser Boston, Massachusetts; 1998:vi+313.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chudziak, J. Approximate solutions of the generalized Gołąb-Schinzel equation. J Inequal Appl 2006, 89402 (2006). https://doi.org/10.1155/JIA/2006/89402
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/JIA/2006/89402
 and a generalization of the Gołąb-Schinzel functional equation. Aequationes Mathematicae 1992,43(1):59–71. 10.1007/BF01840475
and a generalization of the Gołąb-Schinzel functional equation. Aequationes Mathematicae 1992,43(1):59–71. 10.1007/BF01840475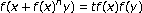 . Publicationes Mathematicae Debrecen 1993,43(1–2):147–160.
. Publicationes Mathematicae Debrecen 1993,43(1–2):147–160.