- Research Article
- Open access
- Published:
On Pečarić-Rajić-Dragomir-Type Inequalities in Normed Linear Spaces
Journal of Inequalities and Applications volume 2009, Article number: 137301 (2009)
Abstract
We establish some generalizations of the recent Pečarić-Rajić-Dragomir-type inequalities by providing upper and lower bounds for the norm of a linear combination of elements in a normed linear space. Our results provide new estimates on inequalities of this type.
1. Introduction
In the recent paper [1], Pečarić and Rajić proved the following inequality for  nonzero vectors
nonzero vectors  ,
,  in the real or complex normed linear space
in the real or complex normed linear space  :
:

and showed that this inequality implies the following refinement of the generalised triangle inequality obtained by Kato et al. in [2]:

The inequality (1.2) can also be obtained as a particular case of Dragomir's result established in [3]:

where  and
and  .
.
Notice that, in [3], a more general inequality for convex functions has been obtained as well.
Recently, the following inequality which is more general than (1.1) was given by Dragomir [4]:

The main aim of this paper is to establish further generalizations of these Pečarić-Rajić-Dragomir-type inequalities (1.1), (1.2), (1.3), and (1.4) by providing upper and lower bounds for the norm of a linear combination of elements in the normed linear space. Our results provide new estimates on such type of inequalities.
2. Main Results
Theorem 2.1.
Let  be a normed linear space over the real or complex number field
be a normed linear space over the real or complex number field  . If
. If  and
and  for
for  with
with  , then
, then

Proof.
Observe that, for any fixed  ,
,  , we have
, we have

Taking the norm in (2.2) and utilizing the triangle inequality, we have

which, on taking the minimum over  ,
,  produces the second inequality in (2.1).
produces the second inequality in (2.1).
Next, by (2.2) we have obviously

On utilizing the continuity property of the norm we also have

which, on taking the maximum over  ,
,  , produces the first part of (2.1) and the theorem is completely proved.
, produces the first part of (2.1) and the theorem is completely proved.
Remark 2.2.
-
(i)
In case the multi-indices
 and
and  reduce to single indices
reduce to single indices  and
and  , respectively, after suitable modifications, (2.1) reduces to inequality (1.4) obtained by Dragomir in [4].
, respectively, after suitable modifications, (2.1) reduces to inequality (1.4) obtained by Dragomir in [4]. -
(ii)
Furthermore, if
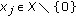 for
for 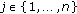 and
and 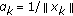 ,
, 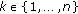 with
with 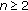 , the inequality reduces further to inequality (1.1) obtained by Pečarić and Rajić in [1].
, the inequality reduces further to inequality (1.1) obtained by Pečarić and Rajić in [1]. -
(iii)
Further to (ii), if
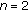 , writing
, writing 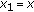 and
and 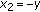 , we have
, we have 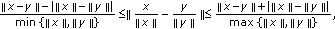 (2.6)
(2.6)
which holds for any nonzero vectors 
The first inequality in (2.6) was obtained by Mercer in [5].
The second inequality in (2.6) has been obtained by Maligranda in [6]. It provides a refinement of the Massera-Schäffer inequality [7]:

which, in turn, is a refinement of the Dunkl-Williams inequality [8]:

Theorem 2.3.
Let  be a normed linear space over the real or complex number field
be a normed linear space over the real or complex number field  . If
. If  and
and  for
for  with
with  , then
, then

This follows immediately from Theorem 2.1 by requiring  for
for  , and letting
, and letting  for
for  ;
;  .
.
A somewhat surprising consequence of Theorem 2.3 is the following version.
Theorem 2.4.
Let  be a normed linear space over the real or complex number field
be a normed linear space over the real or complex number field  . If
. If  for
for  with
with  , then
, then

Proof.
Letting  and by using the second inequality in (2.9), we have
and by using the second inequality in (2.9), we have

Hence

Then it follows that

On the other hand, letting  and by using the first inequality in (2.9), we have
and by using the first inequality in (2.9), we have

Hence

from which we get

This completes the proof.
Remark 2.5.
In case the multi-indices  and
and  reduce to single indices
reduce to single indices  and
and  , respectively, after suitable modifications, (2.10) reduces to inequality (1.2) obtained in [2] by Kato et al.
, respectively, after suitable modifications, (2.10) reduces to inequality (1.2) obtained in [2] by Kato et al.
Theorem 2.6.
Let  be a normed linear space over the real or complex number field
be a normed linear space over the real or complex number field  . If
. If  for
for  with
with  and
and  , then
, then

This follows much in the line as the proofs of Theorem 2.1 and Theorem 2.4, and so it is omitted here.
Remark 2.7.
In case the multi-index  reduces to a single index
reduces to a single index  , after suitable modifications, (2.17) reduces to inequality (1.3) obtained by Dragomir in [3].
, after suitable modifications, (2.17) reduces to inequality (1.3) obtained by Dragomir in [3].
References
Pečarić J, Rajić R: The Dunkl-Williams inequality with
 elements in normed linear spaces. Mathematical Inequalities & Applications 2007,10(2):461–470.
elements in normed linear spaces. Mathematical Inequalities & Applications 2007,10(2):461–470.Kato M, Saito K-S, Tamura T: Sharp triangle inequality and its reverse in Banach spaces. Mathematical Inequalities & Applications 2007,10(2):451–460.
Dragomir SS: Bounds for the normalised Jensen functional. Bulletin of the Australian Mathematical Society 2006,74(3):471–478. 10.1017/S000497270004051X
Dragomir SS: Generalization of the Pečarić-Rajić inequality in normed linear spaces. Mathematical Inequalities & Applications 2009,12(1):53–65.
Mercer PR: The Dunkl-Williams inequality in an inner product space. Mathematical Inequalities & Applications 2007,10(2):447–450.
Maligranda L: Simple norm inequalities. The American Mathematical Monthly 2006,113(3):256–260. 10.2307/27641893
Massera JL, Schäffer JJ: Linear differential equations and functional analysis. I. Annals of Mathematics 1958, 67: 517–573. 10.2307/1969871
Dunkl CF, Williams KS: A simple norm inequality. The American Mathematical Monthly 1964,71(1):53–54. 10.2307/2311304
Acknowledgments
The first author's work is supported by the National Natural Sciences Foundation of China (10971205). The third author's work is partially supported by the Research Grants Council of the Hong Kong SAR, China (Project no. HKU7016/07P).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Changjian, Z., Chen, CJ. & Cheung, WS. On Pečarić-Rajić-Dragomir-Type Inequalities in Normed Linear Spaces. J Inequal Appl 2009, 137301 (2009). https://doi.org/10.1155/2009/137301
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/137301
 and
and  reduce to single indices
reduce to single indices  and
and  , respectively, after suitable modifications, (2.1) reduces to inequality (1.4) obtained by Dragomir in [
, respectively, after suitable modifications, (2.1) reduces to inequality (1.4) obtained by Dragomir in [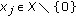 for
for 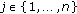 and
and 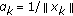 ,
, 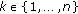 with
with 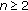 , the inequality reduces further to inequality (1.1) obtained by Pečarić and Rajić in [
, the inequality reduces further to inequality (1.1) obtained by Pečarić and Rajić in [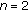 , writing
, writing 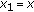 and
and 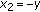 , we have
, we have 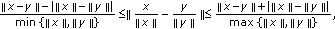
 elements in normed linear spaces. Mathematical Inequalities & Applications 2007,10(2):461–470.
elements in normed linear spaces. Mathematical Inequalities & Applications 2007,10(2):461–470.