- Research
- Open access
- Published:
Existence and uniqueness of periodic solutions of second-order nonlinear differential equations
Journal of Inequalities and Applications volume 2013, Article number: 115 (2013)
Abstract
This paper is concerned with the following second-order nonlinear differential equation:
By applying Mawhin’s continuation theorem of coincidence degree theory, we establish sufficient conditions for the existence and uniqueness of periodic solutions for the above equation. Some recent results are known as the special cases of ours.
1 Introduction
In applied science, some practical problems such as nonlinear oscillations [1, 2], fluid mechanical and nonlinear elastic mechanical phenomena [3–9] are associated with the periodic solutions of nonlinear high-order differential equations. Recently, Bereanu [10], Zhao et al. [11] and Fan et al. [12] investigated the existence of T-periodic solutions for the following fourth-order nonlinear differential equation:
Xu et al. [13] dealt with the existence of T-periodic solutions for the second-order nonlinear differential equation as follows:
where is an even integer, and represent continuous functions, e and g respectively denote the T-periodic and T-periodic in the first argument and . However, to the best of our knowledge, most authors mentioned above have only considered the existence of periodic solutions of Eqs. (1.1) and (1.2). There are still few studies on the uniqueness of periodic solutions for these equations. Thus, in this case, it is worth investigating both the existence and the uniqueness of periodic solutions for a high-order nonlinear differential equation.
In this paper, we study the existence and uniqueness of T-periodic solutions for the second-order nonlinear differential equation
where is an even integer, and represent continuous functions and () are bounded, e and g respectively denote the T-periodic and T-periodic in the first argument and .
Obviously, Eq. (1.1) is a special case of Eq. (1.3) with , , and . Moreover, Eq. (1.2) is another special case of Eq. (1.3) with .
For ease of exposition, we will adopt the following notations throughout this paper:

Let
be Banach spaces with the norms
To obtain our results, we also make the following assumptions:
(S1) There exists such that, for any continuous T-periodic function x, we have
or
(S2) For , ,
(S3) For , , there exists a nonnegative constant B such that
and
2 Preliminaries
The following lemmas will be useful to prove our main results in Section 3.
Let be a continuous function, T-periodic with respect to the first variable, and consider the second-order differential equation

Lemma 2.1 (See [14])
Assume that the following conditions hold.
-
(i)
There exists such that, for each , one has that any possible T-periodic solution x of the problem
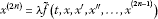
satisfies the a priori estimation .
-
(ii)
The continuous function defined by
satisfies .
Then (2.1) has at least one T-periodic solution x such that .
From Lemma 2.2 in [15] and the proof of inequality (10) in [[12], p.124], we obtain the following.
Lemma 2.2 Let . Suppose that there exist two constants , such that , then
If , then
Lemma 2.4 (See [13])
For any , one has that
Now, let

For , we consider the second-order differential equation

Lemma 2.5 Suppose that (S1), (S2) (or (S3)) hold, then there exists a fixed constant independent of λ and x such that any possible T-periodic solution x of (2.5) satisfies
Proof Let and let x be a possible T-periodic solution of (2.5). Integrating (2.5) from 0 to T yields
which together with (S1) implies that
In view of (2.2) and (2.3), we get
Thus


On the other hand, multiplying Eq. (2.5) by x and integrating it from 0 to T, we obtain
Combining (2.2), (2.3), (2.8) and (2.9), we obtain
Now suppose that (S2) (or (S3)) holds, we will consider two cases as follows.
Case (i). If (S2) holds, then
which implies that there exists a positive constant satisfying
Case (ii). If (S3) holds, (2.2) and (2.3) yield that
which implies (2.10) holds.
Thus, from (2.2), (2.3), (2.4) and (2.10), we can choose a constant independent of λ and x such that
This completes the proof of Lemma 2.5. □
Lemma 2.6 Suppose that (S2) (or (S3)) hold, then (1.3) has at most one T-periodic solution.
Proof Suppose that and are two T-periodic solutions of (1.3). Set . Then we obtain

Integrating (2.11) from 0 to T yields
Therefore, in view of the integral mean value theorem, it follows that there exists a constant such that
From (S2) (or (S3)), we get
which together with (2.2) implies
Multiplying (2.11) by and integrating it from 0 to T, we obtain
Now suppose that (S2) (or (S3)) holds, we will consider two cases as follows.
Case (i). If (S2) holds, (2.3) and (2.13) yield that
which together with (2.3) and (2.12) implies that
Hence, Eq. (1.3) has at most one T-periodic solution.
Case (ii). If (S3) holds, (2.3) and (2.13) yield that
which together with (2.3) and (2.12) implies that
Therefore, Eq. (1.3) has at most one T-periodic solution. The proof of Lemma 2.6 is now completed. □
3 Main results
Theorem 3.1 Let (S1), (S2) (or (S3)) hold and let either or for all , where is constant. Then Eq. (1.3) has a unique T-periodic solution.
Proof From Lemma 2.6, we have obtained that Eq. (1.3) has at most one T-periodic solution. Thus, to prove Theorem 3.1, it suffices to show that Eq. (1.3) has at least one T-periodic solution. To do this, we will use Lemma 2.1. Firstly, let us show that (i) in Lemma 2.1 is satisfied, which means there exists such that any possible T-periodic solution x of (2.5) satisfies
By Lemma 2.5, there exists such that any possible T-periodic solution x of (2.5) satisfies
If , from (2.5), (2.6) and (2.10), it follows that there exists a constant satisfying
which together with (2.4) implies the existence of a constant ρ, such that (3.1) holds.
If , multiplying Eq. (2.5) by and integrating it from 0 to T, we obtain
Therefore, there exists a positive constant satisfying
which together with (2.5), (2.6), (2.10) implies (3.2) holds. Thus, from (2.4) and (3.2), we can also show that (3.1) holds.
Now, to show that (ii) in Lemma 2.1 is satisfied, it suffices to remark that
Hence, from (S1) and , it results that . Then, by Lemma 2.1, we obtain that (1.3) has at least one T-periodic solution x satisfying . This completes the proof. □
4 An example
Example 4.1 Let , , , , , , . Then
has a unique π-periodic solution.
Proof By (4.1), we have , , , , , then
It is obvious that the assumptions (S1), (S2) hold. Hence, by Theorem 3.1, (4.1) has a unique π-periodic solution. □
Example 4.2 Let , , , , , , . Then
has a unique π-periodic solution.
Proof By (4.2), we have , , , , , . Then
It is obvious that the assumptions (S1), (S3) hold. Hence, by Theorem 3.1, (4.2) has a unique π-periodic solution. □
Remark 4.1 Obviously, the authors in [1–13] only considered the existence of periodic solutions of a high-order nonlinear differential equation. Although the author in [18] considered the existence and uniqueness of periodic solutions of high-order nonlinear differential equation, the coefficients of are constants. Hence, the results obtained in [1–13, 18] and the references cited therein are not applicable to Examples 4.1-4.2. This implies that the results of this paper are essentially new.
References
Amster P, Mariani MC: Oscillating solutions of a nonlinear fourth order ordinary differential equation. J. Math. Anal. Appl. 2007, 325: 1133–1141. 10.1016/j.jmaa.2006.02.032
Carriao PC, Faria LFO, Miyagaki OH: Periodic solutions for extended Fisher-Kolmogorov and Swift-Hohenberg equations by truncature techniques. Nonlinear Anal. 2007, 67: 3076–3083. 10.1016/j.na.2006.09.061
Yao Q: Existence, multiplicity and infinite solvability of positive solutions to a nonlinear fourth-order periodic boundary value problem. Nonlinear Anal. 2005, 63: 237–246. 10.1016/j.na.2005.05.009
Chaparova J: Existence and numerical approximations of periodic solutions of semilinear fourth-order differential equations. J. Math. Anal. Appl. 2002, 273: 121–136. 10.1016/S0022-247X(02)00216-0
Mawhin J, Zanolin F: A continuation approach to fourth order superlinear periodic boundary value problems. Topol. Methods Nonlinear Anal. 1993, 2: 55–74.
Peletier LA, Troy WC: Spatial patterns described by the Fisher-Kolmogorov equation: periodic solutions. SIAM J. Math. Anal. 1997, 28: 1317–1353. 10.1137/S0036141095280955
Tersian S, Chaparova J: Periodic and homoclinic solutions of extended Fisher-Kolmogorov equations. J. Math. Anal. Appl. 2001, 260: 490–506. 10.1006/jmaa.2001.7470
Ward JR: Asymptotic conditions for periodic solutions of ordinary differential equations. Proc. Am. Math. Soc. 1981, 81: 415–420. 10.1090/S0002-9939-1981-0597653-2
Li F, Li Y, Liang Z: Existence and multiplicity of solutions to 2 m th-order ordinary differential equations. J. Math. Anal. Appl. 2007, 331: 958–977. 10.1016/j.jmaa.2006.09.025
Bereanu C: Periodic solutions of some fourth-order nonlinear differential equations. Nonlinear Anal. 2009, 71(1–2):53–57. 10.1016/j.na.2008.10.064
Zhao C, Chen W, Zhou J: Periodic solutions for a class of fourth-order nonlinear differential equations. Nonlinear Anal. TMA 2010, 72(3–4):1221–1226. 10.1016/j.na.2009.08.006
Fan Q, Wang W, Zhou J: Periodic solutions of some fourth-order nonlinear differential equations. J. Comput. Appl. Math. 2009, 233(2):121–126. 10.1016/j.cam.2009.07.003
Xu M, Wang W, Yi X: Periodic solutions for a class of nonlinear 2 n th-order differential equations. Nonlinear Anal. 2010, 11: 3399–3405. 10.1016/j.nonrwa.2009.11.030
Mawhin J CBMS Series in Mathematics 40. In Topological Degree Methods in Nonlinear Boundary Value Problems. Am. Math. Soc., Providence; 1979.
Liu B, Huang L: Existence and uniqueness of periodic solutions for a kind of first order neutral functional differential equations. J. Math. Anal. Appl. 2006, 322: 121–132. 10.1016/j.jmaa.2005.08.069
Hardy GH, Littlewood JE, Polya G: Inequalities. Cambridge University Press, London; 1964.
Mawhin J: Periodic solutions of some vector retarded functional differential equations. J. Math. Anal. Appl. 1974, 45: 588–603. 10.1016/0022-247X(74)90053-5
Zhou Q, Gong S: The existence and uniqueness of periodic solutions for some nonlinear n th-order differential equations. Abstr. Appl. Anal. 2012., 2012: Article ID 909387. doi:10.1155/2012/909387
Acknowledgements
The authors would like to express the sincere appreciation to the reviewers for their helpful comments in improving the presentation and quality of the paper. This work was supported by the National Natural Science Foundation of China (grant No. 11201184), the Natural Scientific Research Fund of Hunan Provincial of China (Grant No. 11JJ6006), the Natural Scientific Research Fund of Hunan Provincial Education Department of China (Grant Nos. 11C0916 and 11C0915), and the Natural Scientific Research Fund of Zhejiang Provincial of P.R. China (grant No. LY12A01018).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
RJ gave the proof of Lemma 2.5 and drafted the manuscript. JS proved Theorem 3.1 and gave two examples to illustrate the effectiveness of the obtained results. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jia, R., Shao, J. Existence and uniqueness of periodic solutions of second-order nonlinear differential equations. J Inequal Appl 2013, 115 (2013). https://doi.org/10.1186/1029-242X-2013-115
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2013-115