- Research Article
- Open access
- Published:
On weighted inequalities for parametric Marcinkiewicz integrals
Journal of Inequalities and Applications volume 2006, Article number: 91541 (2006)
Abstract
We establish a weighted boundedness of a parametric Marcinkiewicz integral operator
boundedness of a parametric Marcinkiewicz integral operator if
if is allowed to be in the block space
is allowed to be in the block space for some
for some and
and satisfies a mild integrability condition. We apply this conclusion to obtain the weighted
satisfies a mild integrability condition. We apply this conclusion to obtain the weighted boundedness for a class of the parametric Marcinkiewicz integral operators
boundedness for a class of the parametric Marcinkiewicz integral operators and
and related to the Littlewood-Paley
related to the Littlewood-Paley -function and the area integral
-function and the area integral , respectively. It is known that the condition
, respectively. It is known that the condition is optimal for the
is optimal for the boundedness of
boundedness of .
.
References
Al-Qassem HM:
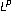 estimates for rough parametric Marcinkiewicz integrals. SUT Journal of Mathematics 2004,40(2):117–131.
estimates for rough parametric Marcinkiewicz integrals. SUT Journal of Mathematics 2004,40(2):117–131.Al-Qassem HM, Al-Salman AJ: A note on Marcinkiewicz integral operators. Journal of Mathematical Analysis and Applications 2003,282(2):698–710. 10.1016/S0022-247X(03)00244-0
Benedek A, Calderón A-P, Panzone R: Convolution operators on Banach space valued functions. Proceedings of the National Academy of Sciences of the United States of America 1962, 48: 356–365. 10.1073/pnas.48.3.356
Chen J, Fan D, Pan Y: A note on a Marcinkiewicz integral operator. Mathematische Nachrichten 2001,227(1):33–42. 10.1002/1522-2616(200107)227:1<33::AID-MANA33>3.0.CO;2-0
Ding Y, Fan D, Pan Y: Weighted boundedness for a class of rough Marcinkiewicz integrals. Indiana University Mathematics Journal 1999,48(3):1037–1055.
Duoandikoetxea J: Weighted norm inequalities for homogeneous singular integrals. Transactions of the American Mathematical Society 1993,336(2):869–880. 10.2307/2154381
Duoandikoetxea J, Rubio de Francia JL: Maximal and singular integral operators via Fourier transform estimates. Inventiones Mathematicae 1986,84(3):541–561. 10.1007/BF01388746
Fan D, Pan Y, Yang D: A weighted norm inequality for rough singular integrals. The Tohoku Mathematical Journal. Second Series 1999,51(2):141–161.
García-Cuerva J, Rubio de Francia JL: Weighted Norm Inequalities and Related Topics, North-Holland Mathematics Studies. Volume 116. North-Holland, Amsterdam; 1985:x+604.
Hörmander L: Estimates for translation invariant operators inspaces
 . Acta Mathematica 1960, 104: 93–140. 10.1007/BF02547187
. Acta Mathematica 1960, 104: 93–140. 10.1007/BF02547187Keitoku M, Sato E: Block spaces on the unit sphere in
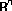 . Proceedings of the American Mathematical Society 1993,119(2):453–455.
. Proceedings of the American Mathematical Society 1993,119(2):453–455.Kurtz DS: Littlewood-Paley and multiplier theorems on weighted
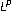 spaces. Transactions of the American Mathematical Society 1980,259(1):235–254.
spaces. Transactions of the American Mathematical Society 1980,259(1):235–254.Lee M-Y, Lin C-C: Weighted
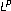 boundedness of Marcinkiewicz integral. Integral Equations and Operator Theory 2004,49(2):211–220. 10.1007/s00020-002-1204-x
boundedness of Marcinkiewicz integral. Integral Equations and Operator Theory 2004,49(2):211–220. 10.1007/s00020-002-1204-xLu S, Taibleson M, Weiss G: Spaces Generated by Blocks. Normal University Press, Beijing; 1989.
Sakamoto M, Yabuta K: Boundedness of Marcinkiewicz functions. Studia Mathematica 1999,135(2):103–142.
Sato S: Remarks on square functions in the Littlewood-Paley theory. Bulletin of the Australian Mathematical Society 1998,58(2):199–211. 10.1017/S0004972700032172
Stein EM: On the functions of Littlewood-Paley, Lusin, and Marcinkiewicz. Transactions of the American Mathematical Society 1958, 88: 430–466. 10.1090/S0002-9947-1958-0112932-2
Stein EM: Singular Integrals and Differentiability Properties of Functions, Princeton Mathematical Series, no. 30. Princeton University Press, New Jersey; 1970:xiv+290.
Torchinsky A, Wang SL: A note on the Marcinkiewicz integral. Colloquium Mathematicum 1990,60/61(1):235–243.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Al-Qassem, H.M. On weighted inequalities for parametric Marcinkiewicz integrals. J Inequal Appl 2006, 91541 (2006). https://doi.org/10.1155/JIA/2006/91541
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/JIA/2006/91541
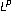 estimates for rough parametric Marcinkiewicz integrals. SUT Journal of Mathematics 2004,40(2):117–131.
estimates for rough parametric Marcinkiewicz integrals. SUT Journal of Mathematics 2004,40(2):117–131. . Acta Mathematica 1960, 104: 93–140. 10.1007/BF02547187
. Acta Mathematica 1960, 104: 93–140. 10.1007/BF02547187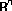 . Proceedings of the American Mathematical Society 1993,119(2):453–455.
. Proceedings of the American Mathematical Society 1993,119(2):453–455.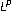 spaces. Transactions of the American Mathematical Society 1980,259(1):235–254.
spaces. Transactions of the American Mathematical Society 1980,259(1):235–254.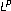 boundedness of Marcinkiewicz integral. Integral Equations and Operator Theory 2004,49(2):211–220. 10.1007/s00020-002-1204-x
boundedness of Marcinkiewicz integral. Integral Equations and Operator Theory 2004,49(2):211–220. 10.1007/s00020-002-1204-x