- Research Article
- Open access
- Published:
On multivalued nonlinear variational inclusion problems with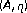 -accretive mappings in Banach spaces
-accretive mappings in Banach spaces
Journal of Inequalities and Applications volume 2006, Article number: 59836 (2006)
Abstract
Based on the notion of -accretive mappings and the resolvent operators associated with
-accretive mappings and the resolvent operators associated with -accretive mappings due to Lan et al., we study a new class of multivalued nonlinear variational inclusion problems with
-accretive mappings due to Lan et al., we study a new class of multivalued nonlinear variational inclusion problems with -accretive mappings in Banach spaces and construct some new iterative algorithms to approximate the solutions of the nonlinear variational inclusion problems involving
-accretive mappings in Banach spaces and construct some new iterative algorithms to approximate the solutions of the nonlinear variational inclusion problems involving -accretive mappings. We also prove the existence of solutions and the convergence of the sequences generated by the algorithms in
-accretive mappings. We also prove the existence of solutions and the convergence of the sequences generated by the algorithms in -uniformly smooth Banach spaces.
-uniformly smooth Banach spaces.
References
Ding XP: Existence and algorithm of solutions for generalized mixed implicit quasi-variational inequalities. Applied Mathematics and Computation 2000,113(1):67–80. 10.1016/S0096-3003(99)00068-5
Fang Y-P, Cho YJ, Kim JK: -accretive operators and approximating solutions for systems of variational inclusions in Banach spaces. to appear in Nonlinear Analysis to appear in Nonlinear Analysis
Fang Y-P, Huang N-J: -monotone operator and resolvent operator technique for variational inclusions. Applied Mathematics and Computation 2003,145(2–3):795–803. 10.1016/S0096-3003(03)00275-3
Fang Y-P, Huang N-J: Approximate solutions for nonlinear operator inclusions with-monotone operators. In Research Report. Sichuan University, Chengdu; 2003.
Fang Y-P, Huang N-J: -accretive operators and resolvent operator technique for solving variational inclusions in Banach spaces. Applied Mathematics Letters 2004,17(6):647–653. 10.1016/S0893-9659(04)90099-7
Fang Y-P, Huang N-J: Iterative algorithm for a system of variational inclusions involving-accretive operators in Banach spaces. Acta Mathematica Hungarica 2005,108(3):183–195. 10.1007/s10474-005-0219-6
Fang Y-P, Huang N-J, Thompson HB: A new system of variational inclusions with-monotone operators in Hilbert spaces. Computers & Mathematics with Applications 2005,49(2–3):365–374. 10.1016/j.camwa.2004.04.037
Huang N-J: Nonlinear implicit quasi-variational inclusions involving generalized-accretive mappings. Archives of Inequalities and Applications 2004,2(4):413–425.
Huang N-J, Fang Y-P: Generalized-accretive mappings in Banach spaces. Journal of Sichuan University 2001,38(4):591–592.
Huang N-J, Fang Y-P: A new class of general variational inclusions involving maximal-monotone mappings. Publicationes Mathematicae Debrecen 2003,62(1–2):83–98.
Lan H-Y, Cho YJ, Verma RU: On nonlinear relaxed cocoercive variational inclusions involving-accretive mappings in Banach spaces. to appear in Computers & Mathematics with Applications to appear in Computers & Mathematics with Applications
Lan H-Y, Huang N-J, Cho YJ: A new method for nonlinear variational inequalities with multi-valued mappings. Archives of Inequalities and Applications 2004,2(1):73–84.
Nadler SB Jr.: Multi-valued contraction mappings. Pacific Journal of Mathematics 1969, 30: 475–488.
Verma RU: -monotonicity and applications to nonlinear variational inclusion problems. Journal of Applied Mathematics and Stochastic Analysis 2004,2004(2):193–195. 10.1155/S1048953304403013
Verma RU: Approximation-solvability of a class of-monotone variational inclusion problems. Journal of the Korean Society for Industrial and Applied Mathematics 2004,8(1):55–66.
Xu HK: Inequalities in Banach spaces with applications. Nonlinear Analysis 1991,16(12):1127–1138. 10.1016/0362-546X(91)90200-K
Zeidler E: Nonlinear Functional Analysis and Its Applications II: Monotone Operators. Springer, Berlin; 1985.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lan, HY. On multivalued nonlinear variational inclusion problems with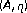 -accretive mappings in Banach spaces.
J Inequal Appl 2006, 59836 (2006). https://doi.org/10.1155/JIA/2006/59836
-accretive mappings in Banach spaces.
J Inequal Appl 2006, 59836 (2006). https://doi.org/10.1155/JIA/2006/59836
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/JIA/2006/59836