- Research Article
- Open access
- Published:
On the System of Nonlinear Mixed Implicit Equilibrium Problems in Hilbert Spaces
Journal of Inequalities and Applications volume 2010, Article number: 437976 (2010)
Abstract
We use the Wiener-Hopf equations and the Yosida approximation notions to prove the existence theorem of a system of nonlinear mixed implicit equilibrium problems (SMIE) in Hilbert spaces. The algorithm for finding a solution of the problem (SMIE) is suggested; the convergence criteria and stability of the iterative algorithm are discussed. The results presented in this paper are more general and are viewed as an extension, refinement, and improvement of the previously known results in the literature.
1. Introduction and Preliminaries
Let  be a real Hilbert space whose inner product and norm are denoted by
be a real Hilbert space whose inner product and norm are denoted by  and
and  respectively. Let
respectively. Let  be given two bi-functions satisfying
be given two bi-functions satisfying  for all
for all  and
and  . Let
. Let  be a nonlinear mapping. Let
be a nonlinear mapping. Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . In this paper, we consider the following problem.
. In this paper, we consider the following problem.
Find  such that
such that

The problem of type (1.1) is called the system of nonlinear mixed implicit equilibrium problems.
We denote by SMIE  the set of all solutions
the set of all solutions  of the problem (1.1).
of the problem (1.1).
Some examples of the problem (1.1) are as follows.
-
(I)
If
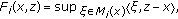 where
where 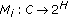 is a maximal monotone mapping for
is a maximal monotone mapping for 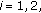 then the problem (1.1) becomes the following problem.
then the problem (1.1) becomes the following problem.
Find  such that
such that

which is called the system of variational inclusion problems. In particular, when  and
and  the problem (1.2) is reduced to the problem, so-called the generalized variational inclusion problem, which was studied by Kazmi and Bhat [1].
the problem (1.2) is reduced to the problem, so-called the generalized variational inclusion problem, which was studied by Kazmi and Bhat [1].
It is worth noting that the variational inclusions and related problems are being studied extensively by many authors and have important applications in operations research, optimization, mathematical finance, decision sciences, and other several branches of pure and applied sciences.
-
(II)
If
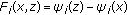 for all
for all  , where
, where 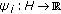 is a real valued function for each
is a real valued function for each  Then the problem (1.1) reduces to the following problem.
Then the problem (1.1) reduces to the following problem.
Find  such that
such that

Some corresponding results to the problem (1.3) were considered by Kassay and Kolumbán [2] when  .
.
-
(III)
For each
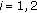 , let
, let 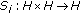 be a nonlinear mapping and
be a nonlinear mapping and  fixed positive real numbers. If
fixed positive real numbers. If  and
and  for all
for all 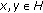 , then the problem (1.3) reduces to the following problem.
, then the problem (1.3) reduces to the following problem.
Find  such that
such that

which is called the system of nonlinear mixed variational inequalities problems. A special case of the problem (1.4), when  and
and  , has been studied by He and Gu [3].
, has been studied by He and Gu [3].
-
(IV)
If
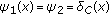 for all
for all 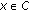 , where
, where 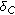 is the indicator function of
is the indicator function of 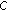 defined by
defined by

then the problem (1.4) reduces to the following problem.
Find  such that
such that

which is called the system of nonlinear variational inequalities problems. Some corresponding results to the problem (1.6) were studied by Agarwal et al. [4], Chang et al. [5], Cho et al. [6], J. K. Kim and D. S. Kim, [7] and Verma [8, 9].
For the recent trends and developments in the problem (1.6) and its special cases, see [3, 8–11] and the references therein, for examples.
-
(V)
If
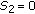 , and
, and  is a univariate mapping, then the problem (1.6) reduces to the following problem.
is a univariate mapping, then the problem (1.6) reduces to the following problem.
Find  such that
such that

which is known as the classical variational inequality introduced and studied by Stampacchia [12] in 1964. This shows that a number of classes of variational inequalities and related optimization problems can be obtained as special cases of the system (1.1) of mixed equilibrium problems.
Inspired and motivated by the recent research going on in this area, in this paper, we use the Wiener-Hopf equations and the Yosida approximation notion to suggest and prove the existence and uniqueness of solutions for the problem (1.1). We also discuss the convergence criteria and stability of the iterative algorithm. The results presented in this paper improve and generalize many known results in the literature.
In the sequel, we need the following basic concepts and lemmas.
Definition 1.1 (Blum and Oettli [13]).
A real valued bifunction  is said to be:
is said to be:

monotone if


strictly monotone if


upper-hemicontinuous if

Definition 1.2.

A function  is said to be lower semicontinuous at
is said to be lower semicontinuous at  if, for all
if, for all  there exists a constant
there exists a constant  such that
such that

where  denotes the ball with center
denotes the ball with center  and radius
and radius  , that is,
, that is,


The function  is said to be lower semicontinuous on
is said to be lower semicontinuous on  if it is lower semicontinuous at every point of
if it is lower semicontinuous at every point of  .
.
Lemma 1.3 (Combettes and Hirstoaga [14]).
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  and
and  be a bifunction of
be a bifunction of  into
into  satisfying the following conditions:
satisfying the following conditions:
(C1) is monotone and upper hemicontinuous;
is monotone and upper hemicontinuous;
(C2)  is convex and lower semi-continuous for all
is convex and lower semi-continuous for all  .
.
For all  and
and  , define a mapping
, define a mapping  as follows:
as follows:

Then  is a single-valued mapping.
is a single-valued mapping.
Definition 1.4.
Let  be a positive number. For any bi-function
be a positive number. For any bi-function  the associated Yosida approximation
the associated Yosida approximation  over
over  and the corresponding regularized operator
and the corresponding regularized operator  are defined as follows:
are defined as follows:

in which  is the unique solution of the following problem:
is the unique solution of the following problem:

Remark 1.5.
Definition 1.4 is an extension of the Yosida approximation notion introduced in [15]. The existence and uniqueness of the solution of the problem (1.15) follow from Lemma 1.3.
Definition 1.6.
Let  be a set-valued mapping.
be a set-valued mapping.

 is said to be monotone if, for any
is said to be monotone if, for any  ,
,


A monotone operator  is said to bemaximal if
is said to bemaximal if  is not properly contained in any other monotone operators.
is not properly contained in any other monotone operators.
Example 1.7 (Huang et al. [16]).
Let  where
where  is a maximal monotone mapping. Then it directly follows that
is a maximal monotone mapping. Then it directly follows that

where  is the Yosida approximation of
is the Yosida approximation of  and we recover the classical concepts.
and we recover the classical concepts.
Using the idea as in Huang et al. [16], we have the following result.
Lemma 1.8.
If  is a monotone function, then the operator
is a monotone function, then the operator  is a nonexpansive mapping, that is,
is a nonexpansive mapping, that is,

Proof.
From (1.15), for all  , we can obtain
, we can obtain


By adding (1.19) with (1.20) and using the monotonicity of  , we have
, we have

and so

This implies that  is a nonexpansive mapping. This completes the proof.
is a nonexpansive mapping. This completes the proof.
Now, for solving the problem (1.1), we consider the following equation: let  and
and  be fixed positive real numbers. Find
be fixed positive real numbers. Find  such that
such that

Lemma 1.9.

is a solution of the problem (1.1) if and only if the problem (1.23) has a solution  where
where

that is,

Proof.
The proof directly follows from the definitions of  and
and  .
.
In this paper, we are interested in the following class of nonlinear mappings.
Definition 1.10.

A mapping  is said to be
is said to be  -strongly monotone if there exists a constant
-strongly monotone if there exists a constant  such that
such that


A mapping  is said to be
is said to be  -Lipschitz if there exist constants
-Lipschitz if there exist constants  such that
such that

2. Existence of Solutions of the Problem (1.1)
In this section, we give an existence theorem of solutions for the problem (1.1). Firstly, in view of Lemma 1.9, we can obtain the following, which is an important tool, immediately.
Lemma 2.1.
Let  . Then
. Then  if and only if there exist positive real numbers
if and only if there exist positive real numbers  such that
such that  is a fixed point of the mapping
is a fixed point of the mapping  defined by
defined by

where  are defined, respectively, by
are defined, respectively, by

Now, we are in position to prove the existence theorem of solutions for the problem (1.1).
Theorem 2.2.
For each  , let
, let  be a monotone bi-function. Let
be a monotone bi-function. Let  be a
be a  -strongly monotone with respect to the first argument and
-strongly monotone with respect to the first argument and  -Lipschitz mapping and
-Lipschitz mapping and  be a
be a  -strongly monotone with respect to the second argument and
-strongly monotone with respect to the second argument and  -Lipschitz mapping. Suppose that there are positive real numbers
-Lipschitz mapping. Suppose that there are positive real numbers  such that
such that

Then  is a singleton.
is a singleton.
Proof.
Notice that, in view of Lemma 2.1, it is sufficient to show that the mapping  defined in Lemma 2.1 has the unique fixed point. Since
defined in Lemma 2.1 has the unique fixed point. Since  is nonexpansive, we have the following estimate:
is nonexpansive, we have the following estimate:

Since  is a
is a  -Lipschitz mapping and, for all
-Lipschitz mapping and, for all  , the mapping
, the mapping  is a
is a  -strongly monotone, we obtain
-strongly monotone, we obtain

Consequently, from (2.4)-(2.5), it follows that

Next, we have the following estimate:

From (2.6) and (2.7), we have

where

Now, define the norm  on
on  by
by

Notice that  is a Banach space and
is a Banach space and

By the condition (2.3), we have  , which implies that
, which implies that  is a contraction mapping. Hence, by Banach contraction principle, there exists a unique
is a contraction mapping. Hence, by Banach contraction principle, there exists a unique  such that
such that  This completes the proof.
This completes the proof.
3. Convergence and Stability Analysis
In view of Lemma 2.1, for the fixed point formulation of the problem (2.1), we suggest the following iterative algorithm.
3.1. Mann Type Perturbed Iterative Algorithm (MTA)
For any  , compute approximate solution
, compute approximate solution  given by the iterative schemes:
given by the iterative schemes:

where  is a sequence of real numbers such that
is a sequence of real numbers such that  and
and 
In order to consider the convergence theorem of the sequences generated by the algorithm (MTA), we need the following lemma.
Lemma 3.1.
Let  and
and  be two nonnegative real sequences satisfying the following conditions. There exists a positive integer
be two nonnegative real sequences satisfying the following conditions. There exists a positive integer  such that
such that

where  with
with  and
and  . Then
. Then 
Now, we prove the convergence theorem for a solution for the problem (1.1).
Theorem 3.2.
If all the conditions of the Theorem 2.2 hold, then the sequence  in
in  generated by the algorithm (3.1) converges strongly to the unique solution for the problem (1.1).
generated by the algorithm (3.1) converges strongly to the unique solution for the problem (1.1).
Proof.
It follows from Theorem 2.2 that there exists  which is the unique solution for the problem (1.1). Moreover, in view of Lemma 2.1, we have
which is the unique solution for the problem (1.1). Moreover, in view of Lemma 2.1, we have

Since  is nonexpansive, from the iterative sequences (3.1) and (3.3), it follows that
is nonexpansive, from the iterative sequences (3.1) and (3.3), it follows that

Next, we have the following estimate:

Substituting (3.5) into (3.4) yields that

Similarly, we have

Thus, from (3.6) and (3.7), we have

where  and
and  are givenin (2.9). Setting
are givenin (2.9). Setting

From the condition (2.3), it follows that  and so
and so  . Moreover, since
. Moreover, since  , we have
, we have  . Hence all the conditions of Lemma 3.1 are satisfied and so
. Hence all the conditions of Lemma 3.1 are satisfied and so  as
as  that is,
that is,

Thus the sequence  in
in  converges strongly to a solution
converges strongly to a solution  for the problem (1.1). This completes the proof.
for the problem (1.1). This completes the proof.
3.2. Stability of the Algorithm (MTA)
Consider the following definition as an extension of the concept of stability of the iterative procedure given by Harder and Hicks [17].
Definition 3.3 (Kazmi and Khan [18]).
Let  be a Hilbert space and
be a Hilbert space and  be nonlinear mappings. Let
be nonlinear mappings. Let  be defined as
be defined as  for all
for all  and
and  . Assume that
. Assume that  defines an iterative procedure which yields a sequence
defines an iterative procedure which yields a sequence  in
in  . Suppose that
. Suppose that  and the sequence
and the sequence  converges to some
converges to some  . Let
. Let  be an arbitrary sequence in
be an arbitrary sequence in  and
and

If  implies that
implies that  , then the iterative procedure
, then the iterative procedure  is said to be
is said to be  -stable or stable with respect to
-stable or stable with respect to  .
.
Theorem 3.4.
Assume that all the conditions of Theorem 2.2 hold. Let  be an arbitrary sequence in
be an arbitrary sequence in  and define
and define  by
by

where

where  is a sequence defined in (3.1). If
is a sequence defined in (3.1). If  is defined as in (2.1), then the iterative procedure generated by (3.1) is
is defined as in (2.1), then the iterative procedure generated by (3.1) is  -stable.
-stable.
Proof.
Assume that  . Let
. Let  be the unique fixed point of the mapping
be the unique fixed point of the mapping  This means that
This means that

Now, from (3.12) and (3.13), it follows that

Notice that  for each
for each  , which implies that
, which implies that

Using (3.16) and the assumption  , it follows from (3.15) that
, it follows from (3.15) that

This completes the proof.
References
Kazmi KR, Bhat MI: Convergence and stability of iterative algorithms for some classes of general variational inclusions in Banach spaces. Southeast Asian Bulletin of Mathematics 2008, 32(1):99–116.
Kassay G, Kolumbán J: System of multi-valued variational inequalities. Publicationes Mathematicae Debrecen 2000, 56(1–2):185–195.
He Z, Gu F: Generalized system for relaxed cocoercive mixed variational inequalities in Hilbert spaces. Applied Mathematics and Computation 2009, 214(1):26–30. 10.1016/j.amc.2009.03.056
Agarwal RP, Cho YJ, Li J, Huang NJ: Stability of iterative procedures with errors approximating common fixed points for a couple of quasi-contractive mappings in -uniformly smooth Banach spaces. Journal of Mathematical Analysis and Applications 2002, 272(2):435–447. 10.1016/S0022-247X(02)00150-6
Chang SS, Joseph Lee HW, Chan CK: Generalized system for relaxed cocoercive variational inequalities in Hilbert spaces. Applied Mathematics Letters 2007, 20(3):329–334. 10.1016/j.aml.2006.04.017
Cho YJ, Fang YP, Huang NJ, Hwang HJ: Algorithms for systems of nonlinear variational inequalities. Journal of the Korean Mathematical Society 2004, 41(3):489–499.
Kim JK, Kim DS: A new system of generalized nonlinear mixed variational inequalities in Hilbert spaces. Journal of Convex Analysis 2004, 11(1):235–243.
Verma RU: Projection methods, algorithms, and a new system of nonlinear variational inequalities. Computers & Mathematics with Applications 2001, 41(7–8):1025–1031. 10.1016/S0898-1221(00)00336-9
Verma RU: Generalized system for relaxed cocoercive variational inequalities and projection methods. Journal of Optimization Theory and Applications 2004, 121(1):203–210.
Nie H, Liu Z, Kim KH, Kang SM: A system of nonlinear variational inequalities involving strongly monotone and pseudocontractive mappings. Advances in Nonlinear Variational Inequalities 2003, 6(2):91–99.
Verma RU: General convergence analysis for two-step projection methods and applications to variational problems. Applied Mathematics Letters 2005, 18(11):1286–1292. 10.1016/j.aml.2005.02.026
Stampacchia G: Formes bilinéaires coercitives sur les ensembles convexes. Comptes Rendus de l'Académie des Sciences: Paris 1964, 258: 4413–4416.
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. The Mathematics Student 1994, 63(1–4):123–145.
Combettes PL, Hirstoaga SA: Equilibrium programming in Hilbert spaces. Journal of Nonlinear and Convex Analysis 2005, 6(1):117–136.
Moudafi A, Théra M: Proximal and dynamical approaches to equilibrium problems. In Ill-Posed Variational Problems and Regularization Techniques (Trier, 1998), Lecture Notes in Economics and Mathematical Systems. Volume 477. Springer, Berlin, Germany; 1999:187–201.
Huang N-J, Lan H, Cho YJ: Sensitivity analysis for nonlinear generalized mixed implicit equilibrium problems with non-monotone set-valued mappings. Journal of Computational and Applied Mathematics 2006, 196(2):608–618. 10.1016/j.cam.2005.10.014
Harder AM, Hicks TL: Stability results for fixed point iteration procedures. Mathematica Japonica 1988, 33(5):693–706.
Kazmi KR, Khan FA: Iterative approximation of a unique solution of a system of variational-like inclusions in real -uniformly smooth Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2007, 67(3):917–929. 10.1016/j.na.2006.06.049
Acknowledgments
The first author was supported by the Korea Research Foundation Grant funded by the Korean Government (KRF-2008-313-C00050). The second author was supported by the Commission on Higher Education and the Thailand Research Fund (project no. MRG5180178).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cho, Y., Petrot, N. On the System of Nonlinear Mixed Implicit Equilibrium Problems in Hilbert Spaces. J Inequal Appl 2010, 437976 (2010). https://doi.org/10.1155/2010/437976
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/437976
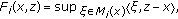 where
where 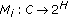 is a maximal monotone mapping for
is a maximal monotone mapping for 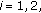 then the problem (1.1) becomes the following problem.
then the problem (1.1) becomes the following problem.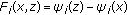 for all
for all  , where
, where 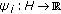 is a real valued function for each
is a real valued function for each  Then the problem (1.1) reduces to the following problem.
Then the problem (1.1) reduces to the following problem.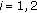 , let
, let 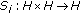 be a nonlinear mapping and
be a nonlinear mapping and  fixed positive real numbers. If
fixed positive real numbers. If  and
and  for all
for all 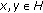 , then the problem (1.3) reduces to the following problem.
, then the problem (1.3) reduces to the following problem.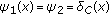 for all
for all 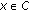 , where
, where 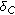 is the indicator function of
is the indicator function of 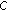 defined by
defined by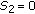 , and
, and  is a univariate mapping, then the problem (1.6) reduces to the following problem.
is a univariate mapping, then the problem (1.6) reduces to the following problem.