- Research Article
- Open access
- Published:
Iterative Refinements of the Hermite-Hadamard Inequality, Applications to the Standard Means
Journal of Inequalities and Applications volume 2010, Article number: 107950 (2010)
Abstract
Two adjacent recursive processes converging to the mean value of a real-valued convex function are given. Refinements of the Hermite-Hadamard inequality are obtained. Some applications to the special means are discussed. A brief extension for convex mappings with variables in a linear space is also provided.
1. Introduction
Let  be a nonempty convex subset of
be a nonempty convex subset of  and let
and let  be a convex function. For
be a convex function. For  , the following double inequality
, the following double inequality

is known in the literature as the Hermite-Hadamard inequality for convex functions. Such inequality is very useful in many mathematical contexts and contributes as a tool for establishing some interesting estimations.
In recent few years, many authors have been interested to give some refinements and extensions of the Hermite-Hadamard inequality (1.1), [1–4]. Dragomir [1] gave a refinement of the left side of (1.1) as summarized in the next result.
Theorem 1.1.
Let  be a convex function and let
be a convex function and let  be defined by
be defined by

Then  is convex increasing on
is convex increasing on  , and for all
, and for all  , one has
, one has

Yang and Hong [3] gave a refinement of the right side of (1.1) as itemized below.
Theorem 1.2.
Let  be a convex function and let
be a convex function and let  be defined by
be defined by

Then  is convex increasing on
is convex increasing on  , and for all
, and for all  , one has
, one has

From the above theorems we immediately deduce the following.
Corollary 1.3.
With the above, there holds

for all  , with
, with

The following refinement of (1.1) is also well-known.
Theorem 1.4.
With the above, the following double inequality holds

For the sake of completeness and in order to explain the key idea of our approach to the reader we will reproduce here the proof of the above known theorem.
Proof.
Applying (1.1) successively in the subintervals  and
and  we obtain
we obtain

The desired result (1.8) follows by adding the above obtained inequalities (1.9).
In [4] Zabandan introduced an improvement of Theorem 1.4 as recited in the following. Let  and
and  be the sequences defined by
be the sequences defined by

Theorem 1.5.
With the above, one has the following inequalities:

with the relationship

Notation 1.
Throughout this paper, and for the sake of presentation, the above expressions  and
and  will be denoted by
will be denoted by  and
and  , and the sequences
, and the sequences  by
by  , respectively. Further, the middle member of inequality (1.1), usually known by the mean value of
, respectively. Further, the middle member of inequality (1.1), usually known by the mean value of  in
in  , will be denoted by
, will be denoted by  , that is,
, that is,

2. Iterative Refinements of the Hermite-Hadamard Inequality
Let  be a nonempty convex subset of
be a nonempty convex subset of  and let
and let  be a convex function. As already pointed out, our fundamental goal in the present section is to give some iterative refinements of (1.1) containing those recalled in the above. We start with our general viewpoint.
be a convex function. As already pointed out, our fundamental goal in the present section is to give some iterative refinements of (1.1) containing those recalled in the above. We start with our general viewpoint.
2.1. General Approach
Examining the proof of Theorem 1.4 we observe that the same procedure can be again recursively applied. More precisely, let us start with the next double inequality

where  are two given functions. Assume that, by the same procedure as in the proof of Theorem 1.4 we have
are two given functions. Assume that, by the same procedure as in the proof of Theorem 1.4 we have

with the following relationships

Reiterating successively the same, we then construct two sequences, denoted by  and
and  , satisfying the following inequalities:
, satisfying the following inequalities:

where  and
and  are defined by the recursive relationships
are defined by the recursive relationships

The initial data  and
and  , which of course depend generally of the convex function
, which of course depend generally of the convex function  , are for the moment upper and lower bounds of inequality (1.1), respectively, and satisfying
, are for the moment upper and lower bounds of inequality (1.1), respectively, and satisfying

Summarizing the previous approach, we may state the following results.
Theorem 2.1.
With the above, the sequence  is increasing and
is increasing and  is a decreasing one. Moreover, the following inequalities:
is a decreasing one. Moreover, the following inequalities:

hold true for all  .
.
Proof.
Follows from the construction of  and
and  . It is also possible to prove the same by using the above recursive relationships defining
. It is also possible to prove the same by using the above recursive relationships defining  and
and  . The proof is complete.
. The proof is complete.
Corollary 2.2.
The sequences  and
and  both converge and their limits are, respectively, the lower and upper bounds of
both converge and their limits are, respectively, the lower and upper bounds of  , that is,
, that is,

Proof.
According to inequalities (2.7), the sequence  is increasing upper bounded by
is increasing upper bounded by  while
while  is decreasing lower bounded by
is decreasing lower bounded by  . It follows that
. It follows that  and
and  both converge. Passing to the limits in inequalities (2.7) we obtain (2.8), which completes the proof.
both converge. Passing to the limits in inequalities (2.7) we obtain (2.8), which completes the proof.
Now, we will observe a question arising naturally from the above study: what is the explicit form of  (and
(and  ) in terms of
) in terms of  ? The answer to this is given in the following result.
? The answer to this is given in the following result.
Theorem 2.3.
With the above, for all  , there hold
, there hold

Proof.
Of course, it is sufficient to show the first formulae which follows from a simple induction with a manipulation on the summation indices. We omit the routine details.
After this, we can put the following question: what are the explicit limits of the sequences  and
and  ? Before giving an answer to this question in a special case, we may state the following examples.
? Before giving an answer to this question in a special case, we may state the following examples.
Example 2.4.
Of course, the first choice of  and
and  is to take the upper and lower bounds of (1.1), respectively, that is,
is to take the upper and lower bounds of (1.1), respectively, that is,

With this choice, we have

which, respectively, correspond to the lower and upper bounds of (1.8). By convexity of  , it is easy to see that the inequalities (2.6) are satisfied. In this case we will prove in the next subsection that
, it is easy to see that the inequalities (2.6) are satisfied. In this case we will prove in the next subsection that  and
and  coincide with
coincide with  and
and  , respectively, and so both converge to
, respectively, and so both converge to  .
.
Example 2.5.
Following Corollary 1.3 we can take

for fixed  ,
,  . It is not hard to verify that the inequalities (2.6) are here satisfied. In this case, our above approach defines us two sequences which depend on the variable
. It is not hard to verify that the inequalities (2.6) are here satisfied. In this case, our above approach defines us two sequences which depend on the variable  . For this, such sequences of functions will be denoted by
. For this, such sequences of functions will be denoted by  and
and  . This example, which contains the above one, will be detailed in the following.
. This example, which contains the above one, will be detailed in the following.
2.2. Case of Example 2.4
Choosing  and
and  as in Example 2.4, we first state the following result.
as in Example 2.4, we first state the following result.
Proposition 2.6.
With (2.10), one has

where  and
and  are given by (1.10).
are given by (1.10).
Proof.
It is a simple verification from formulas (2.9) with (1.10).
Now, we will reproduce to prove that the sequences  and
and  both converge to
both converge to  by adopting our technical approach. In fact, with (2.10) the sequences
by adopting our technical approach. In fact, with (2.10) the sequences  and
and  can be relied by a unique interesting relationship which, as we will see later, will simplify the corresponding proofs. Precisely, we may state the following result.
can be relied by a unique interesting relationship which, as we will see later, will simplify the corresponding proofs. Precisely, we may state the following result.
Proposition 2.7.
Assume that, for  , one has (2.10). Then the following relation holds:
, one has (2.10). Then the following relation holds:

Proof.
It is a simple induction on  and we omit the details for the reader.
and we omit the details for the reader.
Now we are in position to state the following result which gives an answer to the above question when  and
and  are chosen as in Example 2.4.
are chosen as in Example 2.4.
Theorem 2.8.
With (2.10), the sequences  and
and  are adjacent with the limit
are adjacent with the limit

and the following error-estimations hold

Proof.
According to Corollary 2.2, the sequences  and
and  both converge and by the relation (2.14) their limits are equal. Now, by virtue of (2.14) again we can write
both converge and by the relation (2.14) their limits are equal. Now, by virtue of (2.14) again we can write

This, with the inequalities (2.7), yields

By a simple mathematical induction, we simultaneously obtain (2.15) and (2.16). Thus completes the proof.
Remark 2.9.
Starting from a general point of view, we have found again Theorem 1.5 under a new angle and via a technical approach. Furthermore, such approach stems its importance in what follows.
(i)As the reader can remark it, the proofs are here more simple as that of [4] for proving the monotonicity and computing the limit of the considered sequences. See [4, pages 3–5] for such comparison.
(ii)The sequences having  as limit are here defined by simple and recursive relationships which play interesting role in the theoretical study as in the computation context.
as limit are here defined by simple and recursive relationships which play interesting role in the theoretical study as in the computation context.
(iii)Some estimations improving those already stated in the literature are obtained here. In particular, inequalities (2.16) appear to be new for telling us that, in the numerical context, the convergence of  and
and  to
to  is with geometric-speed.
is with geometric-speed.
2.3. Case of Example 2.5
As pointed out before, we can take

for fixed  . The function sequences
. The function sequences  and
and  are defined, for all
are defined, for all  , by the recursive relationships
, by the recursive relationships

By induction, it is not hard to see that the maps  and
and  , for fixed
, for fixed  , are convex and increasing.
, are convex and increasing.
Similarly to the above, we obtain the next result.
Theorem 2.10.
With (2.19), the following assertions are met.
(1)The function sequences  and
and  , for fixed
, for fixed  , are, respectively, monotone increasing and decreasing.
, are, respectively, monotone increasing and decreasing.
(2)For fixed  , the functions
, the functions  and
and  are (convex and) monotonic increasing.
are (convex and) monotonic increasing.
(3)For all  and
and  , one has
, one has

Proof.
-
(1)
By construction, as in the proof of Theorem 2.1.
-
(2)
Comes from the recursive relationships defining
 and
and 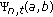 .
. -
(3)
By construction as in the above.
By virtue of the monotonicity of the sequences  ,
,  in a part, and that of the maps
in a part, and that of the maps  ,
,  in another part, the double iterative-functional inequality (2.21) yields some improvements of refinements recalled in the above section. In particular, we immediately find the inequalities (1.3) and (1.6), respectively, by writing
in another part, the double iterative-functional inequality (2.21) yields some improvements of refinements recalled in the above section. In particular, we immediately find the inequalities (1.3) and (1.6), respectively, by writing

for all  , and
, and

for all  .
.
Open Question 2.3.
As we have seen, for every  , the sequences
, the sequences  and
and  both converge. What are their limits? To know if such convergence is uniform on
both converge. What are their limits? To know if such convergence is uniform on  is not obvious and appears also to be interesting.
is not obvious and appears also to be interesting.
3. Applications to Scalar Means
As already pointed out, this section will be devoted to display some applications of the above theoretical results. For this, we need some additional basic notions about special means.
For two nonnegative real numbers  and
and  , the arithmetic, geometric, harmonic, logarithmic, exponential (or identric) means of
, the arithmetic, geometric, harmonic, logarithmic, exponential (or identric) means of  and
and  are, respectively, defined by
are, respectively, defined by

with  . The following inequalities are well known in the literature
. The following inequalities are well known in the literature

When  and
and  are given, the computations of
are given, the computations of  ,
,  and
and  are simple while that of
are simple while that of  and specially that of
and specially that of  are not. So, approaching
are not. So, approaching  and
and  by simple and practical algorithms appears to be interesting. That is the fundamental aim of what follows. In the following applications, we consider the choice (of Example 2.4),
by simple and practical algorithms appears to be interesting. That is the fundamental aim of what follows. In the following applications, we consider the choice (of Example 2.4),

3.1. Application 1: Approximation of the Logarithmic Mean
Consider the convex function  defined by
defined by  . Preserving the same notations as in the previous section, the associate sequences
. Preserving the same notations as in the previous section, the associate sequences  and
and  correspond to the initial data
correspond to the initial data

Applying the above theoretical result to this particular case we immediately obtain the following result.
Theorem 3.1.
The sequences  and
and  , corresponding to
, corresponding to  , both converge to
, both converge to  with the next estimation
with the next estimation

for all  , and the following inequalities hold
, and the following inequalities hold

The above theorem tells us that  containing logarithm can be approached by an iterative algorithm involving only the elementary operations sum, product and inverse. Further, such algorithm is simple, recursive and practical for the numerical context, with a geometric-speed.
containing logarithm can be approached by an iterative algorithm involving only the elementary operations sum, product and inverse. Further, such algorithm is simple, recursive and practical for the numerical context, with a geometric-speed.
3.2. Application 2: Approximation of the Identric Mean
Let  be the convex map
be the convex map  . Writing explicitly the corresponding iterative process
. Writing explicitly the corresponding iterative process  we see that, for reason of simplicity, we may set
we see that, for reason of simplicity, we may set

The auxiliary sequence  is so recursively defined by
is so recursively defined by

As for  , it is easy to establish by a simple induction that
, it is easy to establish by a simple induction that

where the dual sequence  is defined by a similar relationship as
is defined by a similar relationship as  with the initial data
with the initial data  . Our above approach allows us to announce the following interesting result.
. Our above approach allows us to announce the following interesting result.
Theorem 3.2.
The above sequence  converges to
converges to  with the estimation
with the estimation

and the iterative inequalities hold

Furthermore, one has

Proof.
It is immediate from the above general study. The details are left to the reader.
Combining the inequalities of Theorems 3.1 and 3.2, with the fact that  for all
for all  , we simultaneously obtain the known inequalities (3.2). Further, the next result of convergence
, we simultaneously obtain the known inequalities (3.2). Further, the next result of convergence

when  goes to
goes to  , is not obvious to establish directly. This proves again the interest of this work and the generality of our approach.
, is not obvious to establish directly. This proves again the interest of this work and the generality of our approach.
Remark 3.3.
The identric mean  having a transcendent expression is here approached by an algorithm, of algebraic type, utile for the theoretical study and simple for the numerical computation. Further as well-known, to define a non monotone operator mean, via Kubo-Ando theory [5], from the scalar case is not possible. Thus, our approach here could be the key idea for defining the identric mean involving operator and functional variables.
having a transcendent expression is here approached by an algorithm, of algebraic type, utile for the theoretical study and simple for the numerical computation. Further as well-known, to define a non monotone operator mean, via Kubo-Ando theory [5], from the scalar case is not possible. Thus, our approach here could be the key idea for defining the identric mean involving operator and functional variables.
4. Extension for Real-Valued Function with Vector Variable
As well known, the Hermite-Hadamard inequality has an extension for real-valued convex functions with variables in a linear vector space  in the following sense: let
in the following sense: let  be a nonempty convex of
be a nonempty convex of  and let
and let  be a convex function, then for all
be a convex function, then for all  there holds
there holds

In particular, in every linear normed space  , we have
, we have

In general, the computation of the middle side integrals of the above inequalities is not always possible. So, approaching such integrals by recursive and practical algorithms appears to be very interesting. Our aim in this section is to state briefly an analogue of our above approach, with its related fundamental results, for convex functions  . We start with the analogue of Theorem 1.4.
. We start with the analogue of Theorem 1.4.
Theorem 4.1.
Let  be a convex function. Then, for all
be a convex function. Then, for all  ,
,  , there holds
, there holds

where  and
and  are given by
are given by

Proof.
On making the change of variable  , we have
, we have

while for the change of variable  we have
we have

Now, applying the inequality (4.1), we have

If we divide both inequalities with  and add the obtained results we deduce the desired double inequality (4.3).
and add the obtained results we deduce the desired double inequality (4.3).
Similarly, we set

Now, the extension of our above study is itemized in the following statement.
Theorem 4.2.
Let  be a nonempty convex subset of a linear space
be a nonempty convex subset of a linear space  and
and  a convex function. For all
a convex function. For all  , the sequences
, the sequences  and
and  defined by
defined by

are, respectively, monotonic increasing and decreasing and both converge to  with the following estimation
with the following estimation

Proof.
Similar to that of real variables. We omit the details here.
Of course, the sequences  and
and  are relied by similar relation as (2.14) and explicitly given by analogue expressions of (2.9). In particular, we may state the following.
are relied by similar relation as (2.14) and explicitly given by analogue expressions of (2.9). In particular, we may state the following.
Example 4.3.
Let  be a real number and let
be a real number and let  be the convex function defined by
be the convex function defined by  . In this case,
. In this case,  and
and  are given by
are given by

with the following inequalities:

Remark 4.4.
The Hermite-Hadamard inequality, together with some associate refinements, can be extended for nonreal-valued maps that are convex with respect to a given (partial) ordering. In this direction, we indicate the recent paper [6].
References
Dragomir SS: Two mappings in connection to Hadamard's inequalities. Journal of Mathematical Analysis and Applications 1992, 167(1):49–56. 10.1016/0022-247X(92)90233-4
Dragomir SS, McAndrew A: Refinements of the Hermite-Hadamard inequality for convex functions. Journal of Inequalities in Pure and Applied Mathematics 2005., 6(5, article no. 140):
Yang G-S, Hong M-C: A note on Hadamard's inequality. Tamkang Journal of Mathematics 1997, 28(1):33–37.
Zabandan G: A new refinement of the Hermite-Hadamard inequality for convex functions. Journal of Inequalities in Pure and Applied Mathematics 2009., 10(2, article no. 45):
Kubo F, Ando T: Means of positive linear operators. Mathematische Annalen 1980, 246(3):205–224. 10.1007/BF01371042
Dragomir SS, Raïssouli M: Jensen and Hermite-Hadamard inequalities for the Legendre-Fenchel duality, application to convex operator maps. Mathematica Slovaca, 2010, Submitted Mathematica Slovaca, 2010, Submitted
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Dragomir, S., Raïssouli, M. Iterative Refinements of the Hermite-Hadamard Inequality, Applications to the Standard Means. J Inequal Appl 2010, 107950 (2010). https://doi.org/10.1155/2010/107950
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/107950
 and
and 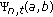 .
.