- Research Article
- Open access
- Published:
Sharpening and Generalizations of Shafer's Inequality for the Arc Tangent Function
Journal of Inequalities and Applications volume 2009, Article number: 930294 (2009)
Abstract
We sharpen and generalize Shafer's inequality for the arc tangent function. From this, some known results are refined.
1. Introduction and Main Results
In [1], the following elementary problem was posed, showing that for  ,
,

In [2], the following three proofs for the inequality (1.1) were provided.
Solution by Grinstein
Direct computation gives

where

Now  is positive for all
is positive for all  ; whence
; whence  is an increasing function.
is an increasing function.
Since  , it follows that
, it follows that  for
for  .
.
Solution by Marsh
It follows from  that
that

The desired result is obtained directly upon integration of the latter inequality with respect to  from
from  to
to  for
for  .
.
Solution by Konhauser
The substitution  transforms the given inequality into
transforms the given inequality into  , which is a special case of an inequality discussed on [3, pages 105-106] .
, which is a special case of an inequality discussed on [3, pages 105-106] .
It may be worthwhile to note that the inequality (1.1) is not collected in the authorized monographs [4, 5].
In [4, pages 288-289], the following inequalities for the arc tangent function are collected:



where  . The inequality (1.5) is better than (1.7).
. The inequality (1.5) is better than (1.7).
The aim of this paper is to sharpen and generalize inequalities (1.1) and (1.5).
Our results may be stated as the following theorems.
Theorem 1.1.
For  , let
, let

where  is a real number.
is a real number.
(1)When  , the function
, the function  is strictly increasing on
is strictly increasing on  .
.
(2)When  , the function
, the function  is strictly decreasing on
is strictly decreasing on  .
.
(3)When  , the function
, the function  has a unique minimum on
has a unique minimum on  .
.
As direct consequences of Theorem 1.1, the following inequalities may be derived.
Theorem 1.2.
For  ,
,

For  ,
,

For  , the inequality (1.9) is reversed.
, the inequality (1.9) is reversed.
Moreover, the constants  and
and  in inequalities (1.9) and (1.10) are the best possible.
in inequalities (1.9) and (1.10) are the best possible.
2. Remarks
Before proving our theorems, we give several remarks on them.
Remark 2.1.
The substitution  may transform inequalities in (1.9) and (1.10) into some trigonometric inequalities.
may transform inequalities in (1.9) and (1.10) into some trigonometric inequalities.
Remark 2.2.
The inequality (1.1) is the special case  of the left-hand side inequality in (1.9).
of the left-hand side inequality in (1.9).
Remark 2.3.
The inequality (1.5) is the special case  of the reversed version of the left hand-side inequality in (1.9).
of the reversed version of the left hand-side inequality in (1.9).
Remark 2.4.
Let

for  and
and  . Direct computation gives
. Direct computation gives

Hence,
(1)when  the derivative
the derivative  is negative for
is negative for  ;
;
(2)when  the derivative
the derivative  has a unique zero which is the unique maximum point of
has a unique zero which is the unique maximum point of  for
for  .
.
Accordingly,
(1)when  the function
the function  attains its maximum
attains its maximum

(2)when  the unique zero of
the unique zero of  equals
equals

and the function  attains its maximum
attains its maximum

for  .
.
In a word, the sharp lower bounds of (1.10) are


for  .
.
Similarly, the sharp upper bound of (1.10) is

Remark 2.5.
Similar to the deduction of inequalities (2.6) and (2.7), the sharp versions of (1.9) and its reversion are


Remark 2.6.
It is easy to verify that the right-hand side inequalities in (2.9) and (2.10) are included in the inequality (2.8).
By the famous software Mathematica, it is revealed that the inequality (2.7) contains (2.6) and the left-hand side inequality in (2.9), and that the inequality (2.7) and the left-hand side inequality in (2.10) are not included in each other.
In conclusion, the following double inequality is the best accurate one:

where  denotes
denotes .
.
Remark 2.7.
For possible applications of the double inequality (2.11) in the theory of approximations, the accuracy of bounds in (2.11) for the arc tangent function is described by Figures 1 and 2.
The upper curves in Figures 1 and 2 are, respectively, the graphs of the functions

and the lower curves in Figures 1 and 2 are, respectively, the graphs of the functions

on the interval  , where
, where  denotes
denotes .
.
These two figures are plotted by the famous software Mathematica 7.0.
Remark 2.8.
The approach below used in the proofs of Theorems 1.1 and 1.2 has been employed in [6–9].
Remark 2.9.
This paper is a revised version of the preprint [10].
3. Proofs of Theorems
Now we are in a position to prove our theorems.
Proof of Theorem 1.1.
Direct calculation gives

Let

then

and the function

has two zeros

Further differentiation yields

This means that the functions  and
and  are increasing on
are increasing on  . From
. From

it follows that
-
(1)
when
 or
or 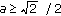 , the derivative
, the derivative 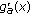 is negative and the function
is negative and the function 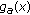 is strictly decreasing on
is strictly decreasing on  . From
. From  (3.8)
(3.8)
it is deduced that  on
on  . Accordingly,
. Accordingly,
(a)when  , the derivative
, the derivative  and the function
and the function  is strictly increasing on
is strictly increasing on  ;
;
(b)when  , the derivative
, the derivative  is negative and the function
is negative and the function  is strictly decreasing on
is strictly decreasing on  ;
;
-
(2)
when
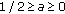 , the derivative
, the derivative 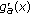 is positive and the function
is positive and the function 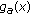 is increasing on
is increasing on  . By (3.8), it follows that the function
. By (3.8), it follows that the function 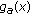 is positive on
is positive on  . Thus, the derivative
. Thus, the derivative 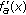 is positive and the function
is positive and the function 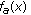 is strictly increasing on
is strictly increasing on  ;
; -
(3)
when
 , the derivative
, the derivative  has a unique zero which is a minimum of
has a unique zero which is a minimum of 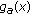 on
on  . Hence, by the second limit in (3.8), it may be deduced that
. Hence, by the second limit in (3.8), it may be deduced that
(a)when  , the function
, the function  is negative on
is negative on  , so the derivative
, so the derivative  is also negative and the function
is also negative and the function  is strictly decreasing on
is strictly decreasing on  ;
;
(b)when  , the function
, the function  has a unique zero which is also a unique zero of the derivative
has a unique zero which is also a unique zero of the derivative  , and so the function
, and so the function  has a unique minimum of the function
has a unique minimum of the function  on
on  .
.
On the other hand, the derivative  can be rewritten as
can be rewritten as

and the function

satisfies

When  , the derivative
, the derivative  is positive and the function
is positive and the function  is strictly increasing on
is strictly increasing on  . Since
. Since  , the function
, the function  is positive, and so the derivative
is positive, and so the derivative  is positive, on
is positive, on  for
for  . Consequently, when
. Consequently, when  , the function
, the function  is strictly increasing on
is strictly increasing on  . The proof of Theorem 1.1 is complete.
. The proof of Theorem 1.1 is complete.
Proof of Theorem 1.2.
Direct calculation yields

By the increasing monotonicity in Theorem 1.1, it follows that  for
for  , which can be rewritten as (1.9) for
, which can be rewritten as (1.9) for  . Similarly, the reversed version of the inequality (1.9) and the right-hand side inequality in (1.10) can be procured.
. Similarly, the reversed version of the inequality (1.9) and the right-hand side inequality in (1.10) can be procured.
When  , the unique minimum point
, the unique minimum point  of the function
of the function  satisfies
satisfies

and so the minimum of  on
on  is
is

where  , as a result, the left-hand side inequality in (1.10) follows. The proof of Theorem 1.2 is complete.
, as a result, the left-hand side inequality in (1.10) follows. The proof of Theorem 1.2 is complete.
References
Thorp EO, Fried M, Shafer RE, et al.: Problems and solutions: elementary problems: E1865-E1874. The American Mathematical Monthly 1966,73(3):309–310. 10.2307/2315358
Shafer RE, Grinstein LS, Marsh DCB, Konhauser JDE: Problems and solutions: solutions of elementary problems: E1867. The American Mathematical Monthly 1967,74(6):726–727.
Mitrinović DS: Elementary Inequalities. P. Noordhoff, Groningen, The Netherlands; 1964:159.
Kuang J-Ch: Chángyòng Bùděngshì (Applied Inequalities), Shāndōng Kēxué Jìshù Chūbăn Shè. 3rd edition. Shandong Science and Technology Press, Ji'nan City, Shandong Province, China; 2004.
Mitrinović DS: Analytic Inequalities. Springer, New York, NY, USA; 1970:xii+400.
Guo B-N, Qi F: Sharpening and generalizations of Carlson's double inequality for the arc cosine function. http://arxiv.org/abs/0902.3039
Qi F, Guo B-N: A concise proof of Oppenheim's double inequality relating to the cosine and sine functions. http://arxiv.org/abs/0902.2511
Qi F, Guo B-N: Concise sharpening and generalizations of Shafer's inequality for the arc sine function. http://arxiv.org/abs/0902.2588
Qi F, Guo B-N: Sharpening and generalizations of Shafer-Fink's double inequality for the arc sine function. http://arxiv.org/abs/0902.3036
Qi F, Guo B-N: Sharpening and generalizations of Shafer's inequality for the arc tangent function. http://arxiv.org/abs/0902.3298
Acknowledgments
The authors appreciate the anonymous referees for their valuable comments that improve this manuscript. The first author was partially supported by the China Scholarship Council.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Qi, F., Zhang, SQ. & Guo, BN. Sharpening and Generalizations of Shafer's Inequality for the Arc Tangent Function. J Inequal Appl 2009, 930294 (2009). https://doi.org/10.1155/2009/930294
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/930294


 or
or 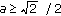 , the derivative
, the derivative 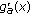 is negative and the function
is negative and the function 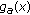 is strictly decreasing on
is strictly decreasing on  . From
. From 
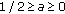 , the derivative
, the derivative 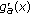 is positive and the function
is positive and the function 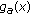 is increasing on
is increasing on  . By (3.8), it follows that the function
. By (3.8), it follows that the function 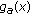 is positive on
is positive on  . Thus, the derivative
. Thus, the derivative 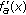 is positive and the function
is positive and the function 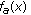 is strictly increasing on
is strictly increasing on  ;
; , the derivative
, the derivative  has a unique zero which is a minimum of
has a unique zero which is a minimum of 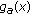 on
on  . Hence, by the second limit in (3.8), it may be deduced that
. Hence, by the second limit in (3.8), it may be deduced that