- Research Article
- Open access
- Published:
Approximately  -Jordan Homomorphisms on Banach Algebras
-Jordan Homomorphisms on Banach Algebras
Journal of Inequalities and Applications volume 2009, Article number: 870843 (2009)
Abstract
Let  , and let
, and let  be two rings. An additive map
be two rings. An additive map  is called
is called  -Jordan homomorphism if
-Jordan homomorphism if  for all
for all  . In this paper, we establish the Hyers-Ulam-Rassias stability of
. In this paper, we establish the Hyers-Ulam-Rassias stability of  -Jordan homomorphisms on Banach algebras. Also we show that (a) to each approximate 3-Jordan homomorphism
-Jordan homomorphisms on Banach algebras. Also we show that (a) to each approximate 3-Jordan homomorphism  from a Banach algebra into a semisimple commutative Banach algebra there corresponds a unique 3-ring homomorphism near to
from a Banach algebra into a semisimple commutative Banach algebra there corresponds a unique 3-ring homomorphism near to  , (b) to each approximate
, (b) to each approximate  -Jordan homomorphism
-Jordan homomorphism  between two commutative Banach algebras there corresponds a unique
between two commutative Banach algebras there corresponds a unique  -ring homomorphism near to
-ring homomorphism near to  for all
for all  .
.
1. Introduction and Preliminaries
Let  be two rings (algebras). An additive map
be two rings (algebras). An additive map  is called n-Jordan homomorphism (n-ring homomorphism) if
is called n-Jordan homomorphism (n-ring homomorphism) if  for all
for all 
 for all
for all  If
If  is a linear n-ring homomorphism, we say that
is a linear n-ring homomorphism, we say that  is n-homomorphism. The concept of n-homomorphisms was studied for complex algebras by Hejazian et al. [1] (see also [2, 3]). A 2-Jordan homomorphism is a Jordan homomorphism, in the usual sense, between rings. Every Jordan homomorphism is an n-Jordan homomorphism, for all
is n-homomorphism. The concept of n-homomorphisms was studied for complex algebras by Hejazian et al. [1] (see also [2, 3]). A 2-Jordan homomorphism is a Jordan homomorphism, in the usual sense, between rings. Every Jordan homomorphism is an n-Jordan homomorphism, for all  (e.g., [4, Lemma 6.3.2]), but the converse is false, in general. For instance, let
(e.g., [4, Lemma 6.3.2]), but the converse is false, in general. For instance, let  be an algebra over
be an algebra over  and let
and let  be a nonzero Jordan homomorphism on
be a nonzero Jordan homomorphism on  . Then,
. Then,  is a 3-Jordan homomorphism. It is easy to check that
is a 3-Jordan homomorphism. It is easy to check that  is not 2-Jordan homomorphism or 4-Jordan homomorphism. The concept of n-Jordan homomorphisms was studied by the first author [5]. A classical question in the theory of functional equations is that "when is it true that a mapping which approximately satisfies a functional equation
is not 2-Jordan homomorphism or 4-Jordan homomorphism. The concept of n-Jordan homomorphisms was studied by the first author [5]. A classical question in the theory of functional equations is that "when is it true that a mapping which approximately satisfies a functional equation  must be somehow close to an exact solution of
must be somehow close to an exact solution of  ?" Such a problem was formulated by Ulam [6] in 1940 and solved in the next year for the Cauchy functional equation by Hyers [7]. It gave rise to the stability theory for functional equations. Subsequently, various approaches to the problem have been introduced by several authors. For the history and various aspects of this theory we refer the reader to monographs [8–12]. Applying a theorem of Hyers [7], Rassias [13], and Gajda [14], Bourgin [15] proved the stability problem of ring homomorphisms between unital Banach algebras. Badora [16] proved the Hyers-Ulam-Rassias stability of ring homomorphisms, which generalizes the result of Bourgin. Recently, Miura et al. [17] proved the Hyers-Ulam-Rassias stability of Jordan homomorphisms. The stability problem of n-homomorphisms between Banach algebras, has been proved by the first author [18]. In this paper, we consider the stability, in the sense of Hyers-Ulam-Rassias, of n-Jordan homomorphisms on Banach algebras.
?" Such a problem was formulated by Ulam [6] in 1940 and solved in the next year for the Cauchy functional equation by Hyers [7]. It gave rise to the stability theory for functional equations. Subsequently, various approaches to the problem have been introduced by several authors. For the history and various aspects of this theory we refer the reader to monographs [8–12]. Applying a theorem of Hyers [7], Rassias [13], and Gajda [14], Bourgin [15] proved the stability problem of ring homomorphisms between unital Banach algebras. Badora [16] proved the Hyers-Ulam-Rassias stability of ring homomorphisms, which generalizes the result of Bourgin. Recently, Miura et al. [17] proved the Hyers-Ulam-Rassias stability of Jordan homomorphisms. The stability problem of n-homomorphisms between Banach algebras, has been proved by the first author [18]. In this paper, we consider the stability, in the sense of Hyers-Ulam-Rassias, of n-Jordan homomorphisms on Banach algebras.
2. Main Result
By a following similar way as in [17], we obtain the next theorem.
Theorem 2.1.
Let  be a normed algebra, let
be a normed algebra, let  be a Banach algebra, let
be a Banach algebra, let  and
and  be nonnegative real numbers, and let
be nonnegative real numbers, and let  be a real numbers such that
be a real numbers such that  or
or  , and that
, and that  . Assume that
. Assume that  satisfies the system of functional inequalities
satisfies the system of functional inequalities


for all  Then, there exists a unique n-Jordan homomorphism
Then, there exists a unique n-Jordan homomorphism  such that
such that

for all 
Proof.
Put  , and
, and  for all
for all  It follows from [13, 14] that
It follows from [13, 14] that  is additive map satisfies (2.3). We will show that
is additive map satisfies (2.3). We will show that  is n-Jordan homomorphism. Since
is n-Jordan homomorphism. Since  it follows from (2.2) that
it follows from (2.2) that

Hence, we have

for all  In other words,
In other words,  is n-Jordan homomorphism. The uniqueness property of
is n-Jordan homomorphism. The uniqueness property of  follows from [13, 14].
follows from [13, 14].
Theorem 2.2.
Let  be a normed algebra, let
be a normed algebra, let  be a Banach algebra, let
be a Banach algebra, let  and
and  be nonnegative real numbers, and let
be nonnegative real numbers, and let  be real numbers such that
be real numbers such that  and
and  . If
. If  is a mapping, with
is a mapping, with  , such that the inequalities (2.1) and (2.2) are valid. Then, there exists a unique n-Jordan homomorphism
, such that the inequalities (2.1) and (2.2) are valid. Then, there exists a unique n-Jordan homomorphism  such that
such that

for all 
Proof.
Assume that  It follows from [13] that there exists an additive map
It follows from [13] that there exists an additive map  satisfies (2.6). It suffices to show that
satisfies (2.6). It suffices to show that  for all
for all  Since
Since  is additive, we get
is additive, we get  and so the case
and so the case  is omitted. Let
is omitted. Let  be arbitrarily. If
be arbitrarily. If  then the proof of Theorem 2.1 works well, and
then the proof of Theorem 2.1 works well, and  Thus we need to consider only the case
Thus we need to consider only the case  Since
Since  it follows from (2.2), that
it follows from (2.2), that

Hence, we have

On the other hand, we have

It follows from (2.8) and (2.9) that

which proves  , whenever
, whenever  This completes the proof.
This completes the proof.
By [17, Theorem 1.1] and [5, Theorem 2.5], we have the following theorem.
Theorem 2.3.
Let  be fixed. Suppose
be fixed. Suppose  is a Banach algebra, which needs not to be commutative, and suppose
is a Banach algebra, which needs not to be commutative, and suppose  is a semisimple commutative Banach algebra. Then, each n-Jordan homomorphism
is a semisimple commutative Banach algebra. Then, each n-Jordan homomorphism  is a n-ring homomorphism.
is a n-ring homomorphism.
Let  be fixed. As a direct corollary, we show that to each approximate n-Jordan homomorphism
be fixed. As a direct corollary, we show that to each approximate n-Jordan homomorphism  from a Banach algebra into a semisimple commutative Banach algebra there corresponds a unique n-ring homomorphism near to
from a Banach algebra into a semisimple commutative Banach algebra there corresponds a unique n-ring homomorphism near to  .
.
Corollary 2.4.
Let  be fixed. Suppose
be fixed. Suppose  is a Banach algebra, which needs not to be commutative, and suppose
is a Banach algebra, which needs not to be commutative, and suppose  is a semisimple commutative Banach algebra. Let
is a semisimple commutative Banach algebra. Let  and
and  be nonnegative real numbers and let
be nonnegative real numbers and let  be a real numbers such that
be a real numbers such that  or
or  and
and  . Assume that
. Assume that  satisfies the system of functional inequalities
satisfies the system of functional inequalities

for all  Then, there exists a unique n-ring homomorphism
Then, there exists a unique n-ring homomorphism  such that
such that

for all 
Proof.
It follows from Theorems 2.1, 2.2, and 2.3.
Theorem 2.5.
Let  be fixed,
be fixed,  be two commutative algebras, and let
be two commutative algebras, and let  be a n-Jordan homomorphism. Then,
be a n-Jordan homomorphism. Then,  is n-ring homomorphism.
is n-ring homomorphism.
Proof.
For  (see [5, Theorem 2.2]). Now suppose
(see [5, Theorem 2.2]). Now suppose  Then,
Then,  is additive and
is additive and  for all
for all  Replacing
Replacing  by
by  to get
to get

Now, replacing  by
by  in (2.13), we obtain that
in (2.13), we obtain that

By (2.13) and (2.14), we get

By (2.15) it follows that

Replacing  by
by  in (2.16), we obtain
in (2.16), we obtain

Replacing  by
by  in (2.17), we get
in (2.17), we get

Hence, we get

By (2.19) it follows that

Replacing  by
by  in (2.20), we obtain
in (2.20), we obtain

Replacing  by
by  in (2.21), we get
in (2.21), we get

Replacing  by
by  in above equality to get
in above equality to get

Replacing  by
by  in (2.23), we obtain
in (2.23), we obtain

Combining (2.23) by (2.24), we get

Replacing  by
by  in (2.25) to obtain
in (2.25) to obtain

replacing  by
by  in (2.26), we get
in (2.26), we get

Now, replace  by
by  in (2.27), we obtain
in (2.27), we obtain

Hence,  is 5-ring homomorphism.
is 5-ring homomorphism.
Corollary 2.6.
Let  be fixed. Suppose
be fixed. Suppose  are commutative Banach algebras. Let
are commutative Banach algebras. Let  and
and  be nonnegative real numbers and let
be nonnegative real numbers and let  be a real numbers such that
be a real numbers such that  or
or  , and
, and  . Assume that
. Assume that  satisfies the system of functional inequalities
satisfies the system of functional inequalities

for all  Then, there exists a unique n-ring homomorphism
Then, there exists a unique n-ring homomorphism  such that
such that

for all 
Proof.
It follows from Theorems 2.1, 2.2, and 2.5.
References
Hejazian S, Mirzavaziri M, Moslehian MS:
 -homomorphisms. Bulletin of the Iranian Mathematical Society 2005,31(1):13–23.
-homomorphisms. Bulletin of the Iranian Mathematical Society 2005,31(1):13–23.Bračič J, Moslehian MS: On automatic continuity of 3-homomorphisms on Banach algebras. Bulletin of the Malaysian Mathematical Sciences Society. Second Series 2007,30(2):195–200.
Park E, Trout J: On the nonexistence of nontrivial involutive -homomorphisms of -algebras. to appear in Transactions of the American Mathematical Society to appear in Transactions of the American Mathematical Society
Palmer ThW: Banach Algebras and the General Theory of ∗-Algebras. Vol. I: Algebras and Banach Algebra, Encyclopedia of Mathematics and Its Applications. Volume 49. Cambridge University Press, Cambridge, Mass, USA; 1994:xii+794.
Eshaghi Gordji M: -Jordan homomorphisms. preprint
Ulam SM: Problems in Modern Mathematics. John Wiley & Sons, New York, NY, USA; 1940.
Hyers DH: On the stability of the linear functional equation. Proceedings of the National Academy of Sciences of the United States of America 1941,27(4):222–224. 10.1073/pnas.27.4.222
Czerwik S: Functional Equations and Inequalities in Several Variables. World Scientific, River Edge, NJ, USA; 2002:x+410.
Faĭziev VA, Rassias ThM, Sahoo PK: The space of (
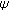 ,
, 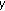 )-additive mappings on semigroups. Transactions of the American Mathematical Society 2002,354(11):4455–4472. 10.1090/S0002-9947-02-03036-2
)-additive mappings on semigroups. Transactions of the American Mathematical Society 2002,354(11):4455–4472. 10.1090/S0002-9947-02-03036-2Hyers DH, Isac G, Rassias ThM: Stability of Functional Equations in Several Variables, Progress in Nonlinear Differential Equations and Their Applications, 34. Birkhäuser, Boston, Mass, USA; 1998:vi+313.
Jung S-M: Hyers-Ulam-Rassias Stability of Functional Equations in Mathematical Analysis. Hadronic Press, Palm Harbor, Fla, USA; 2001:ix+256.
Rassias ThM: On the stability of functional equations and a problem of Ulam. Acta Applicandae Mathematicae 2000,62(1):23–130. 10.1023/A:1006499223572
Rassias ThM: On the stability of the linear mapping in Banach spaces. Proceedings of the American Mathematical Society 1978,72(2):297–300. 10.1090/S0002-9939-1978-0507327-1
Gajda Z: On stability of additive mappings. International Journal of Mathematics and Mathematical Sciences 1991,14(3):431–434. 10.1155/S016117129100056X
Bourgin DG: Approximately isometric and multiplicative transformations on continuous function rings. Duke Mathematical Journal 1949, 16: 385–397. 10.1215/S0012-7094-49-01639-7
Badora R: On approximate derivations. Mathematical Inequalities & Applications 2006,9(1):167–173.
Miura T, Takahasi S-E, Hirasawa G: Hyers-Ulam-Rassias stability of Jordan homomorphisms on Banach algebras. Journal of Inequalities and Applications 2005,2005(4):435–441. 10.1155/JIA.2005.435
Eshaghi Gordji M: On approximate -ring homomorphisms and -ring derivations. preprint
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Gordji, M.E., Karimi, T. & Kaboli Gharetapeh, S. Approximately  -Jordan Homomorphisms on Banach Algebras.
J Inequal Appl 2009, 870843 (2009). https://doi.org/10.1155/2009/870843
-Jordan Homomorphisms on Banach Algebras.
J Inequal Appl 2009, 870843 (2009). https://doi.org/10.1155/2009/870843
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/870843
 -homomorphisms. Bulletin of the Iranian Mathematical Society 2005,31(1):13–23.
-homomorphisms. Bulletin of the Iranian Mathematical Society 2005,31(1):13–23.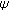 ,
, 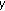 )-additive mappings on semigroups. Transactions of the American Mathematical Society 2002,354(11):4455–4472. 10.1090/S0002-9947-02-03036-2
)-additive mappings on semigroups. Transactions of the American Mathematical Society 2002,354(11):4455–4472. 10.1090/S0002-9947-02-03036-2