- Research Article
- Open access
- Published:
Auxiliary Principle for Generalized Strongly Nonlinear Mixed Variational-Like Inequalities
Journal of Inequalities and Applications volume 2009, Article number: 758786 (2009)
Abstract
We introduce and study a class of generalized strongly nonlinear mixed variational-like inequalities, which includes several classes of variational inequalities and variational-like inequalities as special cases. By applying the auxiliary principle technique and KKM theory, we suggest an iterative algorithm for solving the generalized strongly nonlinear mixed variational-like inequality. The existence of solutions and convergence of sequence generated by the algorithm for the generalized strongly nonlinear mixed variational-like inequalities are obtained. The results presented in this paper extend and unify some known results.
1. Introduction
It is well known that the auxiliary principle technique plays an efficient and important role in variational inequality theory. In 1988, Cohen [1] used the auxiliary principle technique to prove the existence of a unique solution for a variational inequality in reflexive Banach spaces, and suggested an innovative and novel iterative algorithm for computing the solution of the variational inequality. Afterwards, Ding [2], Huang and Deng [3], and Yao [4] obtained the existence of solutions for several kinds of variational-like inequalities. Fang and Huang [5] and Liu et al. [6] discussed some classes of variational inequalities involving various monotone mappings. Recently, Liu et al. [7, 8] extended the auxiliary principle technique to two new classes of variational-like inequalities and established the existence results for these variational-like inequalities.
Inspired and motivated by the results in [1–13], in this paper, we introduce and study a class of generalized strongly nonlinear mixed variational-like inequalities. Making use of the auxiliary principle technique, we construct an iterative algorithm for solving the generalized strongly nonlinear mixed variational-like inequality. Several existence results of solutions for the generalized strongly nonlinear mixed variational-like inequality involving strongly monotone, relaxed Lipschitz, cocoercive, relaxed cocoercive and generalized pseudocontractive mappings, and the convergence results of iterative sequence generated by the algorithm are given. The results presented in this paper extend and unify some known results in [9, 12, 13].
2. Preliminaries
In this paper, let  , let
, let  be a real Hilbert space endowed with an inner product
be a real Hilbert space endowed with an inner product  and norm
and norm  , respectively, let
, respectively, let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Let
. Let 
 and let
and let  be mappings. Now we consider the following generalized strongly nonlinear mixed variational-like inequality problem: find
be mappings. Now we consider the following generalized strongly nonlinear mixed variational-like inequality problem: find  such that
such that

where  is a coercive continuous bilinear form, that is, there exist positive constants
is a coercive continuous bilinear form, that is, there exist positive constants  and
and  such that
such that
(C1)

(C2)
 Clearly,
Clearly, 
Let  satisfy the following conditions:
satisfy the following conditions:
(C3) for each  ,
,  is linear in the first argument;
is linear in the first argument;
(C4) is bounded, that is, there exists a constant
is bounded, that is, there exists a constant  such that
such that 

(C5)
 ;
;
(C6) for each  ,
,  is convex in the second argument.
is convex in the second argument.
Remark 2.1.
It is easy to verify that
(m1)

(m2) ,
,
where (m2) implies that for each  ,
,  is continuous in the second argument on
is continuous in the second argument on  .
.
Special Cases
(m3) If 
 and
and  for all
for all  where
where  , then the generalized strongly nonlinear mixed variational-like inequality (2.1) collapses to seeking
, then the generalized strongly nonlinear mixed variational-like inequality (2.1) collapses to seeking  such that
such that

which was introduced and studied by Ansari and Yao [9], Ding [11] and Zeng [13], respectively.
(m4) If  for all
for all  where
where  , then the problem (2.2) reduces to the following problem: find
, then the problem (2.2) reduces to the following problem: find  such that
such that

which was introduced and studied by Yao [12].
In brief, for suitable choices of the mappings  and
and  , one can obtain a number of known and new variational inequalities and variational-like inequalities as special cases of (2.1). Furthermore, there are a wide classes of problems arising in optimization, economics, structural analysis and fluid dynamics, which can be studied in the general framework of the generalized strongly nonlinear mixed variational-like inequality, which is the main motivation of this paper.
, one can obtain a number of known and new variational inequalities and variational-like inequalities as special cases of (2.1). Furthermore, there are a wide classes of problems arising in optimization, economics, structural analysis and fluid dynamics, which can be studied in the general framework of the generalized strongly nonlinear mixed variational-like inequality, which is the main motivation of this paper.
Definition 2.2.
Let 
 and
and  be mappings.
be mappings.

is said to be relaxed Lipschitz with constant  if there exists a constant
if there exists a constant  such that
such that


is said to be cocoercive with constant  with respect to
with respect to  in the first argument if there exists a constant
in the first argument if there exists a constant  such that
such that


is said to be  -cocoercive with constant
-cocoercive with constant  with respect to
with respect to  in the first argument if there exists a constant
in the first argument if there exists a constant  such that
such that


is said to be relaxed -cocoercive with respect to
-cocoercive with respect to  in the first argument if there exist constants
in the first argument if there exist constants 
 such that
such that


is said to be Lipschitz continuous with constant  if there exists a constant
if there exists a constant  such that
such that


is said to be relaxed Lipschitz with constant  with respect to
with respect to  in the second argument if there exists a constant
in the second argument if there exists a constant  such that
such that


is said to be  -relaxed Lipschitz with constant
-relaxed Lipschitz with constant  with respect to
with respect to  in the second argument if there exists a constant
in the second argument if there exists a constant  such that
such that


is said to be  -generalized pseudocontractive with constant
-generalized pseudocontractive with constant  with respect to
with respect to  in the second argument if there exists a constant
in the second argument if there exists a constant  such that
such that


is said to be strongly monotone with constant  if there exists a constant
if there exists a constant  such that
such that


is said to be relaxed Lipschitz with constant  if there exists a constant
if there exists a constant  such that
such that


is said to be cocoercive with constant  if there exists a constant
if there exists a constant  such that
such that


is said to be Lipschitz continuous with constant  if there exists a constant
if there exists a constant  such that
such that


is said to be Lipschitz continuous in the first argument if there exists a constant  such that
such that

Similarly, we can define the Lipschitz continuity of  in the second argument.
in the second argument.
Definition 2.3.
Let  be a nonempty convex subset of
be a nonempty convex subset of  and let
and let  be a functional.
be a functional.
(d1) is said to be convex if for any
is said to be convex if for any  and any
and any  ,
,

(d2) is said to be concave if
is said to be concave if  is convex;
is convex;
(d3) is said to be lower semicontinuous on
is said to be lower semicontinuous on  if for any
if for any  , the set
, the set  is closed in
is closed in  ;
;
(d4) is said to be upper semicontinuous on
is said to be upper semicontinuous on  , if
, if  is lower semicontinuous on
is lower semicontinuous on  .
.
In order to gain our results, we need the following assumption.
Assumption 2.4.
The mappings 

 satisfy the following conditions:
satisfy the following conditions:
(d5)

(d6) for given  the mapping
the mapping  is concave and upper semicontinuous on
is concave and upper semicontinuous on  .
.
Remark 2.5.
It follows from (d5) and (d6) that
(m5)
(m6) for any given  , the mapping
, the mapping  is convex and lower semicontinuous on
is convex and lower semicontinuous on  .
.
Proposition 2.6 (see [9]).
Let  be a nonempty convex subset of
be a nonempty convex subset of  . If
. If  is lower semicontinuous and convex, then
is lower semicontinuous and convex, then  is weakly lower semicontinuous.
is weakly lower semicontinuous.
Proposition 2.6 yields that if  is upper semicontinuous and concave, then
is upper semicontinuous and concave, then  is weakly upper semicontinuous.
is weakly upper semicontinuous.
Lemma 2.7 (see [10]).
Let  be a nonempty closed convex subset of a Hausdorff linear topological space
be a nonempty closed convex subset of a Hausdorff linear topological space  , and let
, and let  be mappings satisfying the following conditions:
be mappings satisfying the following conditions:
(a) and
and 
-
(b)
for each

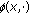 is upper semicontinuous on
is upper semicontinuous on 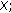
-
(c)
for each
 the set
the set 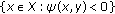 is a convex set
is a convex set
-
(d)
there exists a nonempty compact set
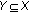 and
and 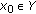 such that
such that 
Then there exists  such that
such that 
3. Auxiliary Problem and Algorithm
In this section, we use the auxiliary principle technique to suggest and analyze an iterative algorithm for solving the generalized strongly nonlinear mixed variational-like inequality (2.1). To be more precise, we consider the following auxiliary problem associated with the generalized strongly nonlinear mixed variational-like inequality (2.1): given  , find
, find  such that
such that

where  is a constant,
is a constant,  is a mapping. The problem is called a auxiliary problem for the generalized strongly nonlinear mixed variational-like inequality (2.1).
is a mapping. The problem is called a auxiliary problem for the generalized strongly nonlinear mixed variational-like inequality (2.1).
Theorem 3.1.
Let  be a nonempty closed convex subset of the Hilbert space
be a nonempty closed convex subset of the Hilbert space  . Let
. Let  be a coercive continuous bilinear form with (C1) and (C2), and let
be a coercive continuous bilinear form with (C1) and (C2), and let  be a functional with (C3)–(C6). Let
be a functional with (C3)–(C6). Let  be Lipschitz continuous and relaxed Lipschitz with constants
be Lipschitz continuous and relaxed Lipschitz with constants  and
and  , respectively. Let
, respectively. Let  be Lipschitz continuous with constant
be Lipschitz continuous with constant  ,
,  and let
and let  satisfy Assumption 2.4. Then the auxiliary problem (3.1) has a unique solution in
satisfy Assumption 2.4. Then the auxiliary problem (3.1) has a unique solution in  .
.
Proof.
For any  , define the mappings
, define the mappings  by
by

We claim that the mappings  and
and  satisfy all the conditions of Lemma 2.7 in the weak topology. Note that
satisfy all the conditions of Lemma 2.7 in the weak topology. Note that

and  for any
for any  Since
Since  is convex in the second argument and
is convex in the second argument and  is a coercive continuous bilinear form, it follows from Remark 2.1 and Assumption 2.4 that for each
is a coercive continuous bilinear form, it follows from Remark 2.1 and Assumption 2.4 that for each  ,
,  is weakly upper semicontinuous on
is weakly upper semicontinuous on  . It is easy to show that the set
. It is easy to show that the set  is a convex set for each fixed
is a convex set for each fixed  Let
Let  be fixed and put
be fixed and put

Clearly,  is a weakly compact subset of
is a weakly compact subset of  . From Assumption 2.4, the continuity of
. From Assumption 2.4, the continuity of  and
and  , and the properties of
, and the properties of  and
and  , we gain that for any
, we gain that for any 

Thus the conditions of Lemma 2.7 are satisfied. It follows from Lemma 2.7 that there exists a  such that
such that  for any
for any  , that is,
, that is,

Let  and
and  . Replacing
. Replacing  by
by  in (3.6) we gain that
in (3.6) we gain that

Letting  in (3.7), we get that
in (3.7), we get that

which means that  is a solution of (3.1).
is a solution of (3.1).
Suppose that  are any two solutions of the auxiliary problem (3.1). It follows that
are any two solutions of the auxiliary problem (3.1). It follows that


Taking  in (3.9) and
in (3.9) and  in (3.10) and adding these two inequalities, we get that
in (3.10) and adding these two inequalities, we get that

Since  is relaxed Lipschitz, we find that
is relaxed Lipschitz, we find that

which implies that  . That is, the auxiliary problem (3.1) has a unique solution in
. That is, the auxiliary problem (3.1) has a unique solution in  . This completes the proof.
. This completes the proof.
Applying Theorem 3.1, we construct an iterative algorithm for solving the generalized strongly nonlinear mixed variational-like inequality (2.1).
Algorithm 3.2.
-
(i)
At step
 , start with the initial value
, start with the initial value 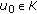 .
. -
(ii)
At step
 , solve the auxiliary problem (3.1) with
, solve the auxiliary problem (3.1) with 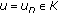 . Let
. Let 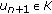 denote the solution of the auxiliary problem (3.1). That is,
denote the solution of the auxiliary problem (3.1). That is, 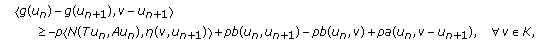 (3.13)
(3.13)
where  is a constant.
is a constant.
-
(iii)
If, for given
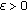 ,
, 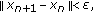 stop. Otherwise, repeat (ii).
stop. Otherwise, repeat (ii).
4. Existence of Solutions and Convergence Analysis
The goal of this section is to prove several existence of solutions and convergence of the sequence generated by Algorithm 3.2 for the generalized strongly nonlinear mixed variational-like inequality (2.1).
Theorem 4.1.
Let  be a nonempty closed convex subset of the Hilbert space
be a nonempty closed convex subset of the Hilbert space  . Let
. Let  be a coercive continuous bilinear form with (C1) and (C2), and let
be a coercive continuous bilinear form with (C1) and (C2), and let  be a functional with (C3)–(C6). Let
be a functional with (C3)–(C6). Let  be Lipschitz continuous with constants
be Lipschitz continuous with constants  in the first and second arguments, respectively. Let
in the first and second arguments, respectively. Let 
 and
and  be Lipschitz continuous with constants
be Lipschitz continuous with constants  respectively, let
respectively, let  be cocoercive with constant
be cocoercive with constant  with respect to
with respect to  in the first argument, let
in the first argument, let  be relaxed Lipschitz with constant
be relaxed Lipschitz with constant  and let
and let  be strongly monotone with constant
be strongly monotone with constant  . Assume that Assumption 2.4 holds. Let
. Assume that Assumption 2.4 holds. Let

If there exists a constant  satisfying
satisfying

and one of the following conditions:




then the generalized strongly nonlinear mixed variational-like inequality (2.1) possesses a solution  and the sequence
and the sequence  defined by Algorithm 3.2 converges to
defined by Algorithm 3.2 converges to 
Proof.
It follows from (3.13) that

Adding (4.7), we obtain that

Since  is relaxed Lipschitz and Lipschitz continuous with constants
is relaxed Lipschitz and Lipschitz continuous with constants  and
and  , and
, and  is strongly monotone and Lipschitz continuous with constants
is strongly monotone and Lipschitz continuous with constants  and
and  , respectively, we get that
, respectively, we get that

Notice that  is Lipschitz continuous in the first and second arguments,
is Lipschitz continuous in the first and second arguments,  and
and  are both Lipschitz continuous, and
are both Lipschitz continuous, and  is cocoercive with constant
is cocoercive with constant  with respect to
with respect to  in the first argument. It follows that
in the first argument. It follows that

Let

It follows from (4.8)–(4.10) that

From (4.2) and one of (4.3)–(4.6), we know that  . It follows from (4.12) that
. It follows from (4.12) that  is a Cauchy sequence in
is a Cauchy sequence in  . By the closedness of
. By the closedness of  there exists
there exists  satisfying
satisfying  . In term of (3.13) and the Lipschitz continuity of
. In term of (3.13) and the Lipschitz continuity of  , we gain that
, we gain that

By Assumption 2.4, we deduce that

Since  as
as  and
and  is bounded, it follows that
is bounded, it follows that

which implies that

In light of (C3) and (m2), we get that

which means that  as
as  . Similarly, we can infer that
. Similarly, we can infer that  as
as  . Therefore,
. Therefore,

This completes the proof.
Theorem 4.2.
Let  and
and  be as in Theorem 4.1. Assume that
be as in Theorem 4.1. Assume that  ,
,  are Lipschitz continuous with constants
are Lipschitz continuous with constants  and
and  , respectively,
, respectively,  is relaxed Lipschitz with constant
is relaxed Lipschitz with constant  , and
, and  is relaxed Lipschitz with constant
is relaxed Lipschitz with constant  with respect to
with respect to  in the second argument. Let
in the second argument. Let

If there exists a constant  satisfying
satisfying

and one of (4.3)–(4.6), then the generalized strongly nonlinear mixed variational-like inequality (2.1) possesses a solution  and the sequence
and the sequence  defined by Algorithm 3.2 converges to
defined by Algorithm 3.2 converges to 
Proof.
As in the proof of Theorem 4.1, we deduce that

Because  is relaxed Lipschitz and Lipschitz continuous,
is relaxed Lipschitz and Lipschitz continuous,  is relaxed Lipschitz with respect to
is relaxed Lipschitz with respect to  in the second argument and Lipschitz continuous, and
in the second argument and Lipschitz continuous, and  is Lipschitz continuous in the second argument, we conclude that
is Lipschitz continuous in the second argument, we conclude that

The rest of the argument is the same as in the proof of Theorem 4.1 and is omitted. This completes the proof.
Theorem 4.3.
Let  and
and  be as in Theorem 4.1, and let
be as in Theorem 4.1, and let  be as in Theorem 4.2. Assume that
be as in Theorem 4.2. Assume that  is
is  -cocoercive with constant
-cocoercive with constant  with respect to
with respect to  in the first argument and Lipschitz continuous with constant
in the first argument and Lipschitz continuous with constant  . Let
. Let

If there exists a constant  satisfying (4.2) and one of (4.3)–(4.6), then the generalized strongly nonlinear mixed variational-like inequality (2.1) possesses a solution
satisfying (4.2) and one of (4.3)–(4.6), then the generalized strongly nonlinear mixed variational-like inequality (2.1) possesses a solution  and the sequence
and the sequence  defined by Algorithm 3.2 converges to
defined by Algorithm 3.2 converges to 
Proof.
As in the proof of Theorem 4.1, we derive that

Because  is Lipschitz continuous,
is Lipschitz continuous,  is Lipschitz continuous in the first argument, and
is Lipschitz continuous in the first argument, and  is
is  -cocoercive with with respect to
-cocoercive with with respect to  in the first argument and Lipschitz continuous, we gain that
in the first argument and Lipschitz continuous, we gain that

The rest of the proof is identical with the proof of Theorem 4.1 and is omitted. This completes the proof.
Theorem 4.4.
Let  and
and  be as in Theorem 4.1. Let
be as in Theorem 4.1. Let  and
and  be as in Theorems 4.2 and 4.3, respectively. Assume that
be as in Theorems 4.2 and 4.3, respectively. Assume that  ,
,  are Lipschitz continuous with constants
are Lipschitz continuous with constants  ,
,  and
and  , respectively,
, respectively,  is g-generalized pseudocontractive with constant
is g-generalized pseudocontractive with constant  with respect to
with respect to  in the second argument, and
in the second argument, and  is cocoercive with constant
is cocoercive with constant  . Let
. Let

If there exists a constant  satisfying
satisfying

and one of (4.3), (4.4), and (4.6), then the generalized strongly nonlinear mixed variational-like inequality (2.1) possesses a solution  and the sequence
and the sequence  defined by Algorithm 3.2 converges to
defined by Algorithm 3.2 converges to 
Proof.
By a similar argument used in the proof of Theorem 4.1, we conclude that

Since  is
is  -generalized pseudocontractive with respect to
-generalized pseudocontractive with respect to  in the second argument and Lipschitz continuous,
in the second argument and Lipschitz continuous,  is Lipschitz continuous and
is Lipschitz continuous and  is Lipschitz continuous in the second argument,
is Lipschitz continuous in the second argument,  is cocoercive and Lipschitz continuous, it follows that
is cocoercive and Lipschitz continuous, it follows that

The rest of the argument follows as in the proof of Theorem 4.1 and is omitted. This completes the proof.
Theorem 4.5.
Let  and
and  be as in Theorem 4.1. Assume that
be as in Theorem 4.1. Assume that  are Lipschitz continuous with constants
are Lipschitz continuous with constants  ,
,  , respectively,
, respectively,  is relaxed
is relaxed  -cocoercive with respect to
-cocoercive with respect to  in the first argument,
in the first argument,  is
is  -relaxed Lipschitz with constant
-relaxed Lipschitz with constant  with respect to
with respect to  in the second argument. Let
in the second argument. Let

If there exists a constant  satisfying
satisfying

and one of (4.3)–(4.6), then the generalized strongly nonlinear mixed variational-like inequality (2.1) possesses a solution  and the sequence
and the sequence  defined by Algorithm 3.2 converges to
defined by Algorithm 3.2 converges to 
Proof.
Notice that

The rest of the proof is similar to the proof of Theorem 4.1 and is omitted. This completes the proof.
Remark 4.6.
Theorems 4.1–4.5 extend, improve, and unify the corresponding results in [9, 12, 13].
References
Cohen G: Auxiliary problem principle extended to variational inequalities. Journal of Optimization Theory and Applications 1988,59(2):325–333.
Ding XP: Existence and algorithm of solutions for nonlinear mixed variational-like inequalities in Banach spaces. Journal of Computational and Applied Mathematics 2003,157(2):419–434. 10.1016/S0377-0427(03)00421-7
Huang N-J, Deng C-X: Auxiliary principle and iterative algorithms for generalized set-valued strongly nonlinear mixed variational-like inequalities. Journal of Mathematical Analysis and Applications 2001,256(2):345–359. 10.1006/jmaa.2000.6988
Yao JC: The generalized quasi-variational inequality problem with applications. Journal of Mathematical Analysis and Applications 1991,158(1):139–160. 10.1016/0022-247X(91)90273-3
Fang YP, Huang NJ: Variational-like inequalities with generalized monotone mappings in Banach spaces. Journal of Optimization Theory and Applications 2003,118(2):327–338. 10.1023/A:1025499305742
Liu Z, Ume JS, Kang SM: General strongly nonlinear quasivariational inequalities with relaxed Lipschitz and relaxed monotone mappings. Journal of Optimization Theory and Applications 2002,114(3):639–656. 10.1023/A:1016079130417
Liu Z, Ume JS, Kang SM: Generalized nonlinear variational-like inequalities in reflexive Banach spaces. Journal of Optimization Theory and Applications 2005,126(1):157–174. 10.1007/s10957-005-2666-1
Liu Z, Chen Z, Kang SM, Ume JS: Existence and iterative approximations of solutions for mixed quasi-variational-like inequalities in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2008,69(10):3259–3272. 10.1016/j.na.2007.09.015
Ansari QH, Yao JC: Iterative schemes for solving mixed variational-like inequalities. Journal of Optimization Theory and Applications 2001,108(3):527–541. 10.1023/A:1017531323904
Chang SS, Xiang SW: On the existence of solutions for a class of quasi-bilinear variational inequalities. Journal of Systems Science and Mathematical Sciences 1996,16(2):136–140.
Ding XP: Algorithm of solutions for mixed-nonlinear variational-like inequalities in reflexive Banach space. Applied Mathematics and Mechanics 1998,19(6):489–496.
Yao JC: Existence of generalized variational inequalities. Operations Research Letters 1994,15(1):35–40. 10.1016/0167-6377(94)90011-6
Zeng L-C: Iterative algorithm for finding approximate solutions of a class of mixed variational-like inequalities. Acta Mathematicae Applicatae Sinica 2004,20(3):477–486. 10.1007/s10255-004-0185-8
Acknowledgments
The authors thank the referees for useful comments and suggestions. This work was supported by the Science Research Foundation of Educational Department of Liaoning Province (2009A419) and the Korea Research Foundation (KRF) grant funded by the Korea government (MEST)(2009-0073655).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Liu, Z., Chen, L., Ume, J.S. et al. Auxiliary Principle for Generalized Strongly Nonlinear Mixed Variational-Like Inequalities. J Inequal Appl 2009, 758786 (2009). https://doi.org/10.1155/2009/758786
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/758786

 is upper semicontinuous on
is upper semicontinuous on 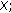
 the set
the set 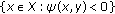 is a convex set
is a convex set
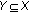 and
and 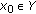 such that
such that 
 , start with the initial value
, start with the initial value 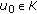 .
. , solve the auxiliary problem (3.1) with
, solve the auxiliary problem (3.1) with 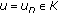 . Let
. Let 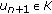 denote the solution of the auxiliary problem (3.1). That is,
denote the solution of the auxiliary problem (3.1). That is, 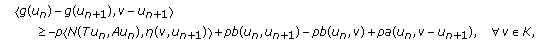
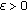 ,
, 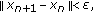 stop. Otherwise, repeat (ii).
stop. Otherwise, repeat (ii).