- Research Article
- Open access
- Published:
Stability of Homomorphisms and Generalized Derivations on Banach Algebras
Journal of Inequalities and Applications volume 2009, Article number: 595439 (2009)
Abstract
We prove the generalized Hyers-Ulam stability of homomorphisms and generalized derivations associated to the following functional equation  on Banach algebras.
on Banach algebras.
1. Introduction
The first stability problem concerning group homomorphisms was raised from a question of Ulam [1]. Let be a group and let
be a group and let be a metric group with the metric
be a metric group with the metric . Given
. Given , does there exist
, does there exist such that if a mapping
such that if a mapping satisfies the inequality
satisfies the inequality

for all , then there is a homomorphism
, then there is a homomorphism with
with

for all

Hyers [2] gave a first affirmative answer to the question of Ulam for Banach spaces. Aoki [3] and Rassias [4] provided a generalization of the Hyers' theorem for additive and linear mappings, respectively, by allowing the Cauchy difference to be unbounded (see also [5]).
Theorem 1.1 (Rassias).
Let  be a mapping from a normed vector space
be a mapping from a normed vector space  into a Banach space
into a Banach space  subject to the inequality
subject to the inequality

for all  , where
, where  and
and  are constants with
are constants with  and
and  . Then the limit
. Then the limit

exists for all  and
and  is the unique additive mapping which satisfies
is the unique additive mapping which satisfies

for all  . If
. If  then inequality (1.3) holds for
then inequality (1.3) holds for  and (1.5) for
and (1.5) for  . Also, if for each
. Also, if for each  the mapping
the mapping  is continuous in
is continuous in  , then
, then  is linear.
is linear.
In 1994, a generalization of the Rassias' theorem was obtained by G vruţa [6], who replaced the bound
vruţa [6], who replaced the bound  by a general control function
by a general control function  For the stability problems of various functional equations and mappings and their Pexiderized versions, we refer the readers to [7–15]. We also refer readers to the books in [16–19].
For the stability problems of various functional equations and mappings and their Pexiderized versions, we refer the readers to [7–15]. We also refer readers to the books in [16–19].
Let  be a real or complex algebra. A mapping
be a real or complex algebra. A mapping  is said to be a(ring) derivation if
is said to be a(ring) derivation if

for all  If, in addition,
If, in addition,  for all
for all  and all
and all  then
then  is called a linear derivation, where
is called a linear derivation, where  denotes the scalar field of
denotes the scalar field of  . Singer and Wermer [20] proved that if
. Singer and Wermer [20] proved that if  is a commutative Banach algebra and
is a commutative Banach algebra and  is a continuous linear derivation, then
is a continuous linear derivation, then  They also conjectured that the same result holds even
They also conjectured that the same result holds even  is a discontinuous linear derivation. Thomas [21] proved the conjecture. As a direct consequence, we see that there are no nonzero linear derivations on a semisimple commutative Banach algebra, which had been proved by Johnson [22]. On the other hand, it is not the case for ring derivations. Hatori and Wada [23] determined a representation of ring derivations on a semi-simple commutative Banach algebra (see also [24]) and they proved that only the zero operator is a ring derivation on a semi-simple commutative Banach algebra with the maximal ideal space without isolated points. The stability of derivations between operator algebras was first obtained by
is a discontinuous linear derivation. Thomas [21] proved the conjecture. As a direct consequence, we see that there are no nonzero linear derivations on a semisimple commutative Banach algebra, which had been proved by Johnson [22]. On the other hand, it is not the case for ring derivations. Hatori and Wada [23] determined a representation of ring derivations on a semi-simple commutative Banach algebra (see also [24]) and they proved that only the zero operator is a ring derivation on a semi-simple commutative Banach algebra with the maximal ideal space without isolated points. The stability of derivations between operator algebras was first obtained by  emrl [25]. Badora [26] and Miura et al. [8] proved the Hyers-Ulam-Rassias stability of ring derivations on Banach algebras. An additive mapping
emrl [25]. Badora [26] and Miura et al. [8] proved the Hyers-Ulam-Rassias stability of ring derivations on Banach algebras. An additive mapping  is called a Jordan derivation in case
is called a Jordan derivation in case  is fulfilled for all
is fulfilled for all  Every derivation is a Jordan derivation. The converse is in general not true (see [27, 28]). The concept of generalized derivation has been introduced by M. Brešar [29]. Hvala [30] and Lee [31] introduced a concept of
Every derivation is a Jordan derivation. The converse is in general not true (see [27, 28]). The concept of generalized derivation has been introduced by M. Brešar [29]. Hvala [30] and Lee [31] introduced a concept of  -derivation (see also [32]). Let
-derivation (see also [32]). Let  be automorphisms of
be automorphisms of  An additive mapping
An additive mapping  is called a
is called a  -derivation in case
-derivation in case  holds for all pairs
holds for all pairs  An additive mapping
An additive mapping  is called a
is called a  -Jordan derivation in case
-Jordan derivation in case  holds for all
holds for all  An additive mapping
An additive mapping  is called a generalized
is called a generalized -derivation in case
-derivation in case  holds for all pairs
holds for all pairs  where
where  is a
is a  -derivation. An additive mapping
-derivation. An additive mapping  is called a generalized
is called a generalized -Jordan derivation in case
-Jordan derivation in case  holds for all
holds for all  where
where  is a
is a  -Jordan derivation. It is clear that every generalized
-Jordan derivation. It is clear that every generalized  -derivation is a generalized
-derivation is a generalized  -Jordan derivation.
-Jordan derivation.
The aim of the present paper is to establish the stability problem of homomorphisms and generalized  -derivations by using the fixed point method (see [7, 33–35]).
-derivations by using the fixed point method (see [7, 33–35]).
Let  be a set. A function
be a set. A function  is called a generalized metric on
is called a generalized metric on  if
if  satisfies
satisfies
(i) if and only if
if and only if  ;
;
(ii) for all
for all  ;
;
(iii) for all
for all 
We recall the following theorem by Margolis and Diaz.
Theorem 1.2 (See [36]).
Let  be a complete generalized metric space and let
be a complete generalized metric space and let  be a strictly contractive mapping with Lipschitz constant
be a strictly contractive mapping with Lipschitz constant  . Then for each given element
. Then for each given element  , either
, either

for all nonnegative integers  or there exists a nonnegative integer
or there exists a nonnegative integer  such that
such that
(1) for all
for all  ;
;
(2)the sequence  converges to a fixed point
converges to a fixed point  of
of  ;
;
(3) is the unique fixed point of
is the unique fixed point of  in the set
in the set  ;
;
(4) for all
for all  .
.
2. Stability of Homomorphisms
Daróczy et al. [37] have studied the functional equation

where  is a fixed parameter and
is a fixed parameter and  is unknown,
is unknown,  is a nonvoid open interval and (2.1) holds for all
is a nonvoid open interval and (2.1) holds for all  They characterized the equivalence of (2.1) and Jensen's functional equation in terms of the algebraic properties of the parameter
They characterized the equivalence of (2.1) and Jensen's functional equation in terms of the algebraic properties of the parameter  For
For  in (2.1), we get the Jensen's functional equation. In the present paper, we establish the general solution and some stability results concerning the functional equation (2.1) in normed spaces for
in (2.1), we get the Jensen's functional equation. In the present paper, we establish the general solution and some stability results concerning the functional equation (2.1) in normed spaces for  This applied to investigate and prove the generalized Hyers-Ulam stability of homomorphisms and generalized derivations in real Banach algebras. In this section, we assume that
This applied to investigate and prove the generalized Hyers-Ulam stability of homomorphisms and generalized derivations in real Banach algebras. In this section, we assume that  is a normed algebra and
is a normed algebra and  is a Banach algebra. For convenience, we use the following abbreviation for a given mapping
is a Banach algebra. For convenience, we use the following abbreviation for a given mapping 

for all  .
.
Lemma 2.1.
Let  and
and  be linear spaces. A mapping
be linear spaces. A mapping  with
with  satisfies
satisfies

for all  if and only if
if and only if  is additive.
is additive.
Proof.
Let  satisfy (2.3). Letting
satisfy (2.3). Letting  in (2.3), we get
in (2.3), we get

for all  Hence
Hence

for all  Letting
Letting  in (2.3), we get
in (2.3), we get  for all
for all  Therefore by (2.5) we have
Therefore by (2.5) we have  for all
for all  This means that
This means that  is odd. Letting
is odd. Letting  in (2.3) and using the oddness of
in (2.3) and using the oddness of  , we infer that
, we infer that  for all
for all  Hence by (2.4) we have
Hence by (2.4) we have  for all
for all  Therefore it follows from (2.3) that
Therefore it follows from (2.3) that  satisfies
satisfies

for all  Replacing
Replacing  and
and  by
by  and
and  in (2.6), respectively, we get
in (2.6), respectively, we get

for all  Replacing
Replacing  by
by  in (2.7) and using the oddness of
in (2.7) and using the oddness of  , we get
, we get

for all  Adding (2.6) to (2.8), we get
Adding (2.6) to (2.8), we get  for all
for all  Using the identity
Using the identity  and replacing
and replacing  by
by  in the last identity, we infer that
in the last identity, we infer that  for all
for all  Hence
Hence  is additive. The converse is obvious.
is additive. The converse is obvious.
Theorem 2.2.
Let  be a mapping with
be a mapping with  for which there exist functions
for which there exist functions  such that
such that



for all  . If there exists a constant
. If there exists a constant  such that
such that

for all  , then there exists a unique (ring) homomorphism
, then there exists a unique (ring) homomorphism  satisfying
satisfying


for all  , where
, where

Proof.
By the assumption, we have

for all  Letting
Letting  in (2.10), we get
in (2.10), we get

for all  Hence
Hence

for all  Letting
Letting  in (2.10), we get
in (2.10), we get

for all  Therefore by (2.18) we have
Therefore by (2.18) we have

for all  Letting
Letting  in (2.10), we get
in (2.10), we get

for all  Now, it follows from (2.20) and (2.21) that
Now, it follows from (2.20) and (2.21) that

for all  Let
Let  We introduce a generalized metric on
We introduce a generalized metric on  as follows:
as follows:

It is easy to show that  is a generalized complete metric space [34].
is a generalized complete metric space [34].
Now we consider the mapping  defined by
defined by

Let  and let
and let  be an arbitrary constant with
be an arbitrary constant with  . From the definition of
. From the definition of  , we have
, we have

for all  . By the assumption and the last inequality, we have
. By the assumption and the last inequality, we have

for all  . So
. So  for any
for any  . It follows from (2.22) that
. It follows from (2.22) that  . Therefore according to Theorem 1.2, the sequence
. Therefore according to Theorem 1.2, the sequence  converges to a fixed point
converges to a fixed point  of
of  , that is,
, that is,

and  for all
for all  . Also
. Also  is the unique fixed point of
is the unique fixed point of  in the set
in the set  and
and

that is, inequality (2.13) holds true for all  . It follows from the definition of
. It follows from the definition of  , (2.10), and (2.16) that
, (2.10), and (2.16) that  for all
for all  Since
Since  by Lemma 2.1 the mapping
by Lemma 2.1 the mapping  is additive. So it follows from the definition of
is additive. So it follows from the definition of  , (2.9), and (2.11) that
, (2.9), and (2.11) that

for all  So
So  is homomorphism. Similarly, we have from (2.9) and (2.11) that
is homomorphism. Similarly, we have from (2.9) and (2.11) that

for all  Since
Since  is homomorphism, we get (2.14) from (2.30).
is homomorphism, we get (2.14) from (2.30).
Finally it remains to prove the uniqueness of  . Let
. Let  another homomorphism satisfying (2.13). Since
another homomorphism satisfying (2.13). Since  and
and  is additive, we get
is additive, we get  and
and  for all
for all  , that is,
, that is,  is a fixed point of
is a fixed point of  . Since
. Since  is the unique fixed point of
is the unique fixed point of  in
in  , we get
, we get 
We need the following lemma in the proof of the next theorem.
Lemma 2.3 (See [38]).
Let  and
and  be linear spaces and
be linear spaces and  be an additive mapping such that
be an additive mapping such that  for all
for all  and all
and all  Then the mapping
Then the mapping  is
is  -linear.
-linear.
Lemma 2.4.
Let  and
and  be linear spaces. A mapping
be linear spaces. A mapping  satisfies
satisfies

for all  and all
and all  if and only if
if and only if  is
is  -linear.
-linear.
Proof.
Let  satisfy (2.31). Letting
satisfy (2.31). Letting  in (2.31), we get
in (2.31), we get  By Lemma 2.1, the mapping
By Lemma 2.1, the mapping  is additive. Letting
is additive. Letting  in (2.31) and using the additivity of
in (2.31) and using the additivity of  we get that
we get that  for all
for all  and all
and all  So by Lemma 2.4, the mapping
So by Lemma 2.4, the mapping  is
is  -linear. The converse is obvious.
-linear. The converse is obvious.
The following theorem is an alternative result of Theorem 2.2 with similar proof.
Theorem 2.5.
Let  be a mapping for which there exist functions
be a mapping for which there exist functions  such that
such that

for all  and all
and all  . If there exists a constant
. If there exists a constant  such that
such that

for all  , then there exists a unique homomorphism
, then there exists a unique homomorphism  satisfying
satisfying

for all  , where
, where  is defined as in Theorem 2.2.
is defined as in Theorem 2.2.
Proof.
It follows from the assumptions that  and so
and so  The rest of the proof is similar to the proof of Theorem 2.2 and we omit the details.
The rest of the proof is similar to the proof of Theorem 2.2 and we omit the details.
Corollary 2.6.
Let  be non-negative real numbers with
be non-negative real numbers with  . Suppose that
. Suppose that  is a mapping such that
is a mapping such that

for all  and all
and all  . Then there exists a unique homomorphism
. Then there exists a unique homomorphism  satisfying
satisfying

for all 
Proof.
The proof follows from Theorem 2.2 by taking

for all  . Then we can choose
. Then we can choose  and we get the desired results.
and we get the desired results.
Corollary 2.7.
Let  be non-negative real numbers with
be non-negative real numbers with  and
and  Suppose that
Suppose that  is a mapping such that
is a mapping such that

for all  and all
and all  . Then there exists a unique homomorphism
. Then there exists a unique homomorphism  satisfying
satisfying

for all 
Proof.
The proof follows from Theorem 2.5 by taking

for all  . Then we can choose
. Then we can choose  and we get the desired results.
and we get the desired results.
3. Stability of Generalized 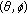 -Derivations
-Derivations
In this section, we assume that  is a Banach algebra, and
is a Banach algebra, and  are automorphisms of
are automorphisms of  For convenience, we use the following abbreviation for given mappings
For convenience, we use the following abbreviation for given mappings 

for all  . Now we prove the generalized Hyers-Ulam stability of generalized
. Now we prove the generalized Hyers-Ulam stability of generalized  -derivations and generalized
-derivations and generalized  -Jordan derivations in Banach algebras.
-Jordan derivations in Banach algebras.
Theorem 3.1.
Let  be mappings with
be mappings with  for which there exists a function
for which there exists a function  such that
such that




for all  . If there exists a constants
. If there exists a constants  such
such

for all  , then there exist a unique
, then there exist a unique  -Jordan derivation
-Jordan derivation  and a unique generalized
and a unique generalized  -Jordan derivation
-Jordan derivation  satisfying
satisfying

for all  , where
, where  is defined as in Theorem 2.2.
is defined as in Theorem 2.2.
Proof.
It follows from the assumptions that

for all  By the proof of Theorem 2.5, there exist unique additive mappings
By the proof of Theorem 2.5, there exist unique additive mappings  satisfying (3.7) and
satisfying (3.7) and

for all  . It follows from the definitions of
. It follows from the definitions of  (3.3), and (3.8) that
(3.3), and (3.8) that

for all  Hence
Hence

for all  Hence
Hence  is a
is a  -Jordan derivation and
-Jordan derivation and  is a generalized
is a generalized  -Jordan derivation.
-Jordan derivation.
Remark 3.2.
Applying Theorem 3.1 for the case  , there exist a unique
, there exist a unique  -Jordan derivation
-Jordan derivation  and a unique generalized
and a unique generalized  -Jordan derivation
-Jordan derivation  satisfying
satisfying

for all  .
.
The following theorem is an alternative result of Theorem 3.1 with similar proof.
Theorem 3.3.
Let  be mappings with
be mappings with  for which there exists a function
for which there exists a function  satisfying (3.2)–(3.5). If there exists a constant
satisfying (3.2)–(3.5). If there exists a constant  such
such

for all  , then there exist a unique
, then there exist a unique  -Jordan derivation
-Jordan derivation  and a unique generalized
and a unique generalized  -Jordan derivation
-Jordan derivation  satisfying
satisfying

for all  , where
, where  is defined as in Theorem 2.2.
is defined as in Theorem 2.2.
Remark 3.4.
Applying Theorem 3.3 for the case  , there exist a unique
, there exist a unique  -Jordan derivation
-Jordan derivation  and a unique generalized
and a unique generalized  -Jordan derivation
-Jordan derivation  satisfying
satisfying

for all  .
.
References
Ulam SM: A Collection of Mathematical Problems, Interscience Tracts in Pure and Applied Mathematics, no. 8. Interscience, New York, NY, USA; 1960:xiii+150.
Hyers DH: On the stability of the linear functional equation. Proceedings of the National Academy of Sciences of the United States of America 1941, 27: 222–224. 10.1073/pnas.27.4.222
Aoki T: On the stability of the linear transformation in Banach spaces. Journal of the Mathematical Society of Japan 1950, 2: 64–66. 10.2969/jmsj/00210064
Rassias ThM: On the stability of the linear mapping in Banach spaces. Proceedings of the American Mathematical Society 1978,72(2):297–300. 10.1090/S0002-9939-1978-0507327-1
Bourgin DG: Classes of transformations and bordering transformations. Bulletin of the American Mathematical Society 1951, 57: 223–237. 10.1090/S0002-9904-1951-09511-7
Găvruţa P: A generalization of the Hyers-Ulam-Rassias stability of approximately additive mappings. Journal of Mathematical Analysis and Applications 1994,184(3):431–436. 10.1006/jmaa.1994.1211
Mirzavaziri M, Moslehian MS: A fixed point approach to stability of a quadratic equation. Bulletin of the Brazilian Mathematical Society 2006,37(3):361–376. 10.1007/s00574-006-0016-z
Miura T, Hirasawa G, Takahasi S-E: A perturbation of ring derivations on Banach algebras. Journal of Mathematical Analysis and Applications 2006,319(2):522–530. 10.1016/j.jmaa.2005.06.060
Moslehian MS: Hyers-Ulam-Rassias stability of generalized derivations. International Journal of Mathematics and Mathematical Sciences 2006, 2006:-8.
Najati A: Hyers-Ulam stability of an
 -Apollonius type quadratic mapping. Bulletin of the Belgian Mathematical Society. Simon Stevin 2007,14(4):755–774.
-Apollonius type quadratic mapping. Bulletin of the Belgian Mathematical Society. Simon Stevin 2007,14(4):755–774.Najati A: On the stability of a quartic functional equation. Journal of Mathematical Analysis and Applications 2008,340(1):569–574. 10.1016/j.jmaa.2007.08.048
Najati A, Moghimi MB: Stability of a functional equation deriving from quadratic and additive functions in quasi-Banach spaces. Journal of Mathematical Analysis and Applications 2008,337(1):399–415. 10.1016/j.jmaa.2007.03.104
Najati A, Park C: Hyers-Ulam-Rassias stability of homomorphisms in quasi-Banach algebras associated to the Pexiderized Cauchy functional equation. Journal of Mathematical Analysis and Applications 2007,335(2):763–778. 10.1016/j.jmaa.2007.02.009
Najati A, Park C: On the stability of an
 -dimensional functional equation originating from quadratic forms. Taiwanese Journal of Mathematics 2008,12(7):1609–1624.
-dimensional functional equation originating from quadratic forms. Taiwanese Journal of Mathematics 2008,12(7):1609–1624.Park C: On the stability of the linear mapping in Banach modules. Journal of Mathematical Analysis and Applications 2002,275(2):711–720. 10.1016/S0022-247X(02)00386-4
Czerwik P: Functional Equations and Inequalities in Several Variables. World Scientific, River Edge, NJ, USA; 2002:x+410.
Hyers DH, Isac G, Rassias TM: Stability of Functional Equations in Several Variables, Progress in Nonlinear Differential Equations and Their Applications, 34. Birkhäuser, Boston, Mass, USA; 1998:vi+313.
Jung S-M: Hyers-Ulam-Rassias Stability of Functional Equations in Mathematical Analysis. Hadronic Press, Palm Harbor, Fla, USA; 2001:ix+256.
Rassias ThM: Functional Equations, Inequalities and Applications. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2003:x+224.
Singer IM, Wermer J: Derivations on commutative normed algebras. Mathematische Annalen 1955, 129: 260–264. 10.1007/BF01362370
Thomas MP: The image of a derivation is contained in the radical. Annals of Mathematics 1988,128(3):435–460. 10.2307/1971432
Johnson BE: Continuity of derivations on commutative algebras. American Journal of Mathematics 1969, 91: 1–10. 10.2307/2373262
Hatori O, Wada J: Ring derivations on semi-simple commutative Banach algebras. Tokyo Journal of Mathematics 1992,15(1):223–229. 10.3836/tjm/1270130262
Šemrl P: On ring derivations and quadratic functionals. Aequationes Mathematicae 1991,42(1):80–84. 10.1007/BF01818480
Šemrl P: The functional equation of multiplicative derivation is superstable on standard operator algebras. Integral Equations and Operator Theory 1994,18(1):118–122. 10.1007/BF01225216
Badora R: On approximate derivations. Mathematical Inequalities & Applications 2006,9(1):167–173.
Cusack JM: Jordan derivations on rings. Proceedings of the American Mathematical Society 1975,53(2):321–324. 10.1090/S0002-9939-1975-0399182-5
Herstein IN: Jordan derivations of prime rings. Proceedings of the American Mathematical Society 1957, 8: 1104–1110. 10.1090/S0002-9939-1957-0095864-2
Brešar M: Jordan derivations on semiprime rings. Proceedings of the American Mathematical Society 1988,104(4):1003–1006.
Hvala B: Generalized derivations in rings. Communications in Algebra 1998,26(4):1147–1166. 10.1080/00927879808826190
Lee T-K: Generalized derivations of left faithful rings. Communications in Algebra 1999,27(8):4057–4073. 10.1080/00927879908826682
Liu C-K, Shiue W-K: Generalized Jordan triple
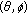 -derivations on semiprime rings. Taiwanese Journal of Mathematics 2007,11(5):1397–1406.
-derivations on semiprime rings. Taiwanese Journal of Mathematics 2007,11(5):1397–1406.Amyari M, Moslehian MS: Hyers-Ulam-Rassias stability of derivations on Hilbert
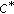 -modules. In Topological Algebras and Applications, Contemporary Mathematics. Volume 427. American Mathematical Society, Providence, RI, USA; 2007:31–39.
-modules. In Topological Algebras and Applications, Contemporary Mathematics. Volume 427. American Mathematical Society, Providence, RI, USA; 2007:31–39.Cădariu L, Radu V: On the stability of the Cauchy functional equation: a fixed point approach. In Iteration Theory, Grazer Mathematische Berichte. Volume 346. Karl-Franzens-Universitaet Graz, Graz, Austria; 2004:43–52.
Jung S-M, Kim T-S: A fixed point approach to the stability of the cubic functional equation. Boletín de la Sociedad Matemática Mexicana 2006,12(1):51–57.
Diaz JB, Margolis B: A fixed point theorem of the alternative, for contractions on a generalized complete metric space. Bulletin of the American Mathematical Society 1968, 74: 305–309. 10.1090/S0002-9904-1968-11933-0
Daróczy Z, Lajkó K, Lovas RL, Maksa Gy, Páles Zs: Functional equations involving means. Acta Mathematica Hungarica 2007,116(1–2):79–87. 10.1007/s10474-007-5296-2
Park C: Homomorphisms between Poisson
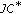 -algebras. Bulletin of the Brazilian Mathematical Society 2005,36(1):79–97. 10.1007/s00574-005-0029-z
-algebras. Bulletin of the Brazilian Mathematical Society 2005,36(1):79–97. 10.1007/s00574-005-0029-z
Acknowledgment
The second author was supported by Hanyang University in 2009.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Najati, A., Park, C. Stability of Homomorphisms and Generalized Derivations on Banach Algebras. J Inequal Appl 2009, 595439 (2009). https://doi.org/10.1155/2009/595439
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/595439
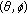 -Derivations
-Derivations -Apollonius type quadratic mapping. Bulletin of the Belgian Mathematical Society. Simon Stevin 2007,14(4):755–774.
-Apollonius type quadratic mapping. Bulletin of the Belgian Mathematical Society. Simon Stevin 2007,14(4):755–774. -dimensional functional equation originating from quadratic forms. Taiwanese Journal of Mathematics 2008,12(7):1609–1624.
-dimensional functional equation originating from quadratic forms. Taiwanese Journal of Mathematics 2008,12(7):1609–1624.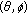 -derivations on semiprime rings. Taiwanese Journal of Mathematics 2007,11(5):1397–1406.
-derivations on semiprime rings. Taiwanese Journal of Mathematics 2007,11(5):1397–1406.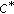 -modules. In Topological Algebras and Applications, Contemporary Mathematics. Volume 427. American Mathematical Society, Providence, RI, USA; 2007:31–39.
-modules. In Topological Algebras and Applications, Contemporary Mathematics. Volume 427. American Mathematical Society, Providence, RI, USA; 2007:31–39.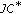 -algebras. Bulletin of the Brazilian Mathematical Society 2005,36(1):79–97. 10.1007/s00574-005-0029-z
-algebras. Bulletin of the Brazilian Mathematical Society 2005,36(1):79–97. 10.1007/s00574-005-0029-z