- Research Article
- Open access
- Published:
A Note on Hölder Type Inequality for the Fermionic 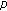 -Adic Invariant
-Adic Invariant  -Integral
-Integral
Journal of Inequalities and Applications volume 2009, Article number: 357349 (2009)
Abstract
The purpose of this paper is to find Hölder type inequality for the fermionic  -adic invariant
-adic invariant  -integral which was defined by Kim (2008).
-integral which was defined by Kim (2008).
1. Introduction
Let  be a fixed odd prime. Throughout this paper
be a fixed odd prime. Throughout this paper  ,
,  ,
,  and
and  will, respectively, denote the ring of
will, respectively, denote the ring of  -adic rational integers, the field of
-adic rational integers, the field of  -adic rational numbers, the rational number field, the complex number field, and the completion of algebraic closure of
-adic rational numbers, the rational number field, the complex number field, and the completion of algebraic closure of  . For a fixed positive integer
. For a fixed positive integer  with
with  , let
, let

Let  be the set of natural numbers. In this paper we assume that
be the set of natural numbers. In this paper we assume that  with
with  , which implies that
, which implies that  for
for  . We also use the notations
. We also use the notations

for all  . For any positive integer
. For any positive integer  the distribution is defined by
the distribution is defined by

We say that  is a uniformly differentiable function at a point
is a uniformly differentiable function at a point  and denote this property by
and denote this property by  , if the difference quotients
, if the difference quotients  have a limit
have a limit  as
as  (cf. [1–24]).
(cf. [1–24]).
For  , the above distribution
, the above distribution  yields the bosonic
yields the bosonic  -adic invariant
-adic invariant  -integral as follows:
-integral as follows:

representing the  -adic
-adic  -analogue of the Riemann integral for
-analogue of the Riemann integral for  . In the sense of fermionic, let us define the fermionic
. In the sense of fermionic, let us define the fermionic  -adic invariant
-adic invariant  -integral on
-integral on  as
as

for  (see [16]). Now, we consider the fermionic
(see [16]). Now, we consider the fermionic  -adic invariant
-adic invariant  -integral on
-integral on  as
as

From (1.5) we note that

where  (see [16]).
(see [16]).
We also introduce the classical Hölder inequality for the Lebesgue integral in [25].
Theorem 1.1.
Let  with
with  . If
. If  and
and  , then
, then  and
and

where  and
and  and
and  .
.
The purpose of this paper is to find Hölder type inequality for the fermionic  -adic invariant
-adic invariant  -integral
-integral  .
.
2. Hölder Type Inequality for Fermionic 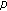 -Adic Invariant
-Adic Invariant 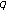 -Integrals
-Integrals
In order to investigate the Hölder type inequality for  , we introduce the new concept of the inequality as follows.
, we introduce the new concept of the inequality as follows.
Definition 2.1.
For  , we define the inequality on
, we define the inequality on  (resp.,
(resp.,  ) as follows. For
) as follows. For  (resp.,
(resp.,  ),
),  (resp.,
(resp.,  ) if and only if
) if and only if  (resp.,
(resp.,  ).
).
Let  with
with  . By substituting
. By substituting  and
and  into
into  , we obtain the following equation:
, we obtain the following equation:



From (2.1), (2.2), and (2.3), we derive

We remark that the  th Frobenius-Euler numbers
th Frobenius-Euler numbers  and the
and the  th Frobenius-Euler polynomials
th Frobenius-Euler polynomials  attached to algebraic number
attached to algebraic number  may be defined by the exponential generating functions (see [16]):
may be defined by the exponential generating functions (see [16]):


Then, it is easy to see that

From (2.4) and (2.7), we have the following theorem.
Theorem 2.2.
Let  with
with  . If one takes
. If one takes  and
and  , then one has
, then one has

We note that for  with
with  ,
,

By Theorem 2.2 and (2.7) and the definition of  -adic norm, it is easy to see that
-adic norm, it is easy to see that

for all  with
with  . We note that
. We note that  lies in
lies in  . Thus by Definition 2.1 and (2.10), we obtain the following Hölder type inequality theorem for fermionic
. Thus by Definition 2.1 and (2.10), we obtain the following Hölder type inequality theorem for fermionic  -adic invariant
-adic invariant  -integrals.
-integrals.
Theorem 2.3.
Let  with
with  and
and  . If one takes
. If one takes  and
and  , then one has
, then one has

References
Cenkci M, Simsek Y, Kurt V: Further remarks on multiple -adic --function of two variables. Advanced Studies in Contemporary Mathematics 2007,14(1):49–68.
Jang L-C: A new -analogue of Bernoulli polynomials associated with -adic -integrals. Abstract and Applied Analysis 2008, 2008:-6.
Jang L-C, Kim S-D, Park D-W, Ro Y-S: A note on Euler number and polynomials. Journal of Inequalities and Applications 2006, 2006:-5.
Kim T: -Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288–299.
Kim T: 0 -integrals associated with multiple Changhee -Bernoulli polynomials. Russian Journal of Mathematical Physics 2003,10(1):91–98.
Kim T: On Euler-Barnes multiple zeta functions. Russian Journal of Mathematical Physics 2003,10(3):261–267.
Kim T: Analytic continuation of multiple -zeta functions and their values at negative integers. Russian Journal of Mathematical Physics 2004,11(1):71–76.
Kim T: Power series and asymptotic series associated with the -analog of the two-variable -adic -function. Russian Journal of Mathematical Physics 2005,12(2):186–196.
Kim T: Multiple -adic -function. Russian Journal of Mathematical Physics 2006,13(2):151–157. 10.1134/S1061920806020038
Kim T: -generalized Euler numbers and polynomials. Russian Journal of Mathematical Physics 2006,13(3):293–298. 10.1134/S1061920806030058
Kim T: Lebesgue-Radon-Nikod\'ym theorem with respect to -Volkenborn distribution on . Applied Mathematics and Computation 2007,187(1):266–271. 10.1016/j.amc.2006.08.123
Kim T: -extension of the Euler formula and trigonometric functions. Russian Journal of Mathematical Physics 2007,14(3):275–278. 10.1134/S1061920807030041
Kim T: -Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51–57.
Kim T: An invariant -adic -integral on . Applied Mathematics Letters 2008,21(2):105–108. 10.1016/j.aml.2006.11.011
Kim T: An identity of the symmetry for the Frobenius-Euler polynomials associated with the Fermionic -adic invariant -integrals on . to appear in Rocky Mountain Journal of Mathematics, http://arxiv.org/abs/0804.4605 to appear in Rocky Mountain Journal of Mathematics,
Kim T: Symmetry -adic invariant integral on for Bernoulli and Euler polynomials. Journal of Difference Equations and Applications 2008,14(12):1267–1277. 10.1080/10236190801943220
Kim T, Choi JY, Sug JY: Extended -Euler numbers and polynomials associated with fermionic -adic -integral on . Russian Journal of Mathematical Physics 2007,14(2):160–163. 10.1134/S1061920807020045
Kim T, Kim M-S, Jang L-C, Rim S-H: New -Euler numbers and polynomials associated with -adic -integrals. Advanced Studies in Contemporary Mathematics 2007,15(2):243–252.
Kim T, Simsek Y: Analytic continuation of the multiple Daehee --functions associated with Daehee numbers. Russian Journal of Mathematical Physics 2008,15(1):58–65.
Ozden H, Simsek Y, Rim S-H, Cangul IN: A note on -adic -Euler measure. Advanced Studies in Contemporary Mathematics 2007,14(2):233–239.
Rim S-H, Kim T: A note on -adic Euler measure on . Russian Journal of Mathematical Physics 2006,13(3):358–361. 10.1134/S1061920806030113
Simsek Y: On -adic twisted --functions related to generalized twisted Bernoulli numbers. Russian Journal of Mathematical Physics 2006,13(3):340–348. 10.1134/S1061920806030095
Simsek Y: Generating functions of the twisted Bernoulli numbers and polynomials associated with their interpolation functions. Advanced Studies in Contemporary Mathematics 2008,16(2):251–278.
Srivastava HM, Kim T, Simsek Y: -Bernoulli numbers and polynomials associated with multiple -zeta functions and basic -series. Russian Journal of Mathematical Physics 2005,12(2):241–268.
Royden HL: Real Analysis. Prentice-Hall, Englewood Cliffs, NJ, USA; 1998.
Acknowledgment
This paper was supported by the KOSEF 2009-0073396.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jang, LC. A Note on Hölder Type Inequality for the Fermionic 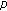 -Adic Invariant
-Adic Invariant  -Integral.
J Inequal Appl 2009, 357349 (2009). https://doi.org/10.1155/2009/357349
-Integral.
J Inequal Appl 2009, 357349 (2009). https://doi.org/10.1155/2009/357349
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/357349
 lies in
lies in  (cf. [
(cf. [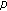 -Adic Invariant
-Adic Invariant 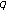 -Integrals
-Integrals