- Research Article
- Open access
- Published:
Regularity of Parabolic Hemivariational Inequalities with Boundary Conditions
Journal of Inequalities and Applications volume 2009, Article number: 207873 (2009)
Abstract
We prove the regularity for solutions of parabolic hemivariational inequalities of dynamic elasticity in the strong sense and investigate the continuity of the solution mapping from initial data and forcing term to trajectories.
1. Introduction
In this paper, we deal with the existence and a variational of constant formula for solutions of a parabolic hemivariational inequality of the form:





where  is a bounded domain in
is a bounded domain in  with sufficiently smooth boundary
with sufficiently smooth boundary  Let
Let  ,
,  ,
,  The boundary
The boundary  is composed of two pieces
is composed of two pieces  and
and  , which are nonempty sets and defined by
, which are nonempty sets and defined by

where  is the unit outward normal vector to
is the unit outward normal vector to  . Here
. Here  ,
,  is the displacement,
is the displacement,  is the strain tensor,
is the strain tensor,  ,
,  is a multi-valued mapping by filling in jumps of a locally bounded function
is a multi-valued mapping by filling in jumps of a locally bounded function  ,
,  . A continuous map
. A continuous map  from the space
from the space  of
of  symmetric matrices into itself is defined by
symmetric matrices into itself is defined by

where  is the identity of
is the identity of  ,
,  denotes the trace of
denotes the trace of  , and
, and  ,
,  . For example, in the case
. For example, in the case  ,
,  , where
, where  is Young's modulus,
is Young's modulus,  is Poisson's ratio and
is Poisson's ratio and  is the density of the plate.
is the density of the plate.
Let  and
and  be two complex Hilbert spaces. Assume that
be two complex Hilbert spaces. Assume that  is a dense subspace in
is a dense subspace in  and the injection of
and the injection of  into
into  is continuous. Let
is continuous. Let  be a continuous linear operator from
be a continuous linear operator from  into
into  which is assumed to satisfy Gårding's inequality. Namely, we formulated the problem (1.1) as
which is assumed to satisfy Gårding's inequality. Namely, we formulated the problem (1.1) as

The existence of global weak solutions for a class of hemivariational inequalities has been studied by many authors, for example, parabolic type problems in [1–4], and hyperbolic types in [5–7]. Rauch [8] and Miettinen and Panagiotopoulos [1, 2] proved the existence of weak solutions for elliptic one. The background of these variational problems are physics, especially in solid mechanics, where nonconvex and multi-valued constitutive laws lead to differential inclusions. We refer to [3, 4] to see the applications of differential inclusions. Most of them considered the existence of weak solutions for differential inclusions of various forms by using the Faedo-Galerkin approximation method.
In this paper, we prove the existence and a variational of constant formula for strong solutions of parabolic hemivariational inequalities. The plan of this paper is as follows. In Section 2, the main results besides notations and assumptions are stated. In order to prove the solvability of the linear case with  we establish necessary estimates applying the result of Di Blasio et al. [9] to (1.1)–(1.5) considered as an equation in
we establish necessary estimates applying the result of Di Blasio et al. [9] to (1.1)–(1.5) considered as an equation in  as well as
as well as  . The existence and regularity for the nondegenerate nonlinear systems has been developed as seen in [10, Theorem 4.1] or [11, Theorem 2.6], and the references therein. In Section 3, we will obtain the existence for solutions of (1.1)–(1.5) by converting the problem into the contraction mapping principle and the norm estimate of a solution of the above nonlinear equation on
. The existence and regularity for the nondegenerate nonlinear systems has been developed as seen in [10, Theorem 4.1] or [11, Theorem 2.6], and the references therein. In Section 3, we will obtain the existence for solutions of (1.1)–(1.5) by converting the problem into the contraction mapping principle and the norm estimate of a solution of the above nonlinear equation on  . Consequently, if
. Consequently, if  is a solution asociated with
is a solution asociated with  , and
, and  , in view of the monotonicity of
, in view of the monotonicity of  , we show that the mapping
, we show that the mapping

is continuous.
2. Preliminaries and Linear Hemivariational Inequalities
We denote  for
for  ,
,  and
and  for
for  . Throughout this paper, we consider
. Throughout this paper, we consider

We denote  the dual space of
the dual space of  ,
,  the dual pairing between
the dual pairing between  and
and  .
.
The norms on  ,
,  , and
, and  will be denoted by
will be denoted by  ,
,  and
and  , respectively. For the sake of simplicity, we may consider
, respectively. For the sake of simplicity, we may consider

We denote  by
by  . Let
. Let  be the operator associated with a sesquilinear form
be the operator associated with a sesquilinear form  which is defined Gårding's inequality
which is defined Gårding's inequality

that is,

Then  is a symmetric bounded linear operator from
is a symmetric bounded linear operator from  into
into  which satisfies
which satisfies

and its realization in  which is the restriction of
which is the restriction of  to
to

is also denoted by  . Here, we note that
. Here, we note that  is dense in
is dense in  . Hence, it is also dense in
. Hence, it is also dense in  . We endow the domain
. We endow the domain  of
of  with graph norm, that is, for
with graph norm, that is, for  , we define
, we define  . So, for the brevity, we may regard that
. So, for the brevity, we may regard that  for all
for all  . It is known that—
. It is known that— generates an analytic semigroup
generates an analytic semigroup  in both
in both  and
and  .
.
From the following inequalities

it follows that there exists a constant  such that
such that

So, we may regard as  where
where  is the real interpolation space between
is the real interpolation space between  and
and  .
.
Consider the following initial value problem for the abstract linear parabolic type equation:

A continuous map  from the space
from the space  of
of  symmetric matrices into itself is defined by
symmetric matrices into itself is defined by

It is easily known that


Note that the map  is linear and symmetric and it can be easily verified that the tensor
is linear and symmetric and it can be easily verified that the tensor  satisfies the condition
satisfies the condition

Let  be the smallest positive constant such that
be the smallest positive constant such that

Simple calculations and Korn's inequality yield that

and hence  is equivalent to the
is equivalent to the  norm on
norm on  Then by virtue of [9, Theorem 3.3], we have the following result on the linear parabolic type equation (LE).
Then by virtue of [9, Theorem 3.3], we have the following result on the linear parabolic type equation (LE).
Proposition 2.1.
Suppose that the assumptions stated above are satisfied. Then the following properties hold.
(1)For any  and
and  , there exists a unique solution
, there exists a unique solution  of (LE) belonging to
of (LE) belonging to

and satisfying

where  is a constant depending on
is a constant depending on  .
.
(2)Let  and
and  for any
for any  . Then there exists a unique solution
. Then there exists a unique solution  of (LE) belonging to
of (LE) belonging to

and satisfying

where  is a constant depending on
is a constant depending on  .
.
Proof.
-
(1)
Let
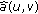 be a bounded sesquilinear form defined in
be a bounded sesquilinear form defined in  by
by 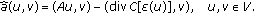 (2.19)
(2.19)
Noting that by(2.10)

and by (2.12), (2.14), and (1.6),

it follows that there exist  and
and  such that
such that

Let  be the operator associated with this sesquilinear form:
be the operator associated with this sesquilinear form:

Then  is also a symmetric continuous linear operator from
is also a symmetric continuous linear operator from  into
into  which satisfies
which satisfies

So we know that— generates an analytic semigroup
generates an analytic semigroup  in both
in both  and
and  . Hence, by applying [9, Theorem 3.3] to the regularity for the solution of the equation:
. Hence, by applying [9, Theorem 3.3] to the regularity for the solution of the equation:

in the space  , we can obtain a unique solution
, we can obtain a unique solution  of (LE) belonging to
of (LE) belonging to

and satisfying the norm estimate (2.16).
-
(2)
It is easily seen that
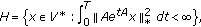 (2.27)
(2.27)
for the time  . Therefore, in terms of the intermediate theory we can see that
. Therefore, in terms of the intermediate theory we can see that

and follow the argument of (1) term by term to deduce the proof of (2) results.
3. Existence of Solutions in the Strong Sense
This Section is to investigate the regularity of solutions for the following parabolic hemivariational inequality of dynamic elasticity in the strong sense:

Now, we formulate the following assumptions.
(Hb) Let  be a locally bounded function verifying
be a locally bounded function verifying

where  We denote
We denote

The multi-valued function  is obtained by filling in jumps of a function
is obtained by filling in jumps of a function  by means of the functions
by means of the functions  as follows.
as follows.

We denote  ,
,  for
for  . We will need a regularization of
. We will need a regularization of  defined by
defined by

where  and
and  It is easy to show that
It is easy to show that  is continuous for all
is continuous for all  and
and  satisfy the same condition (Hb) with possibly different constants if
satisfy the same condition (Hb) with possibly different constants if  satisfies (Hb). It is also known that
satisfies (Hb). It is also known that  is locally Lipschitz continuous in
is locally Lipschitz continuous in  , that is for any
, that is for any  , there exists a number
, there exists a number  such that
such that
(Hb-1)

holds for all  with
with  We denote
We denote

The following lemma is from [[12]; Lemma A.5].
Lemma 3.1.
Let  satisfying
satisfying  for all
for all  and
and  be a constant. Let
be a constant. Let  be a continuous function on
be a continuous function on  satisfying the following inequality:
satisfying the following inequality:

Then,

Proof.
Let

Then

and

Hence, we have

Since  is absolutely continuous and
is absolutely continuous and

for all  , it holds
, it holds

that is,

Therefore, combining this with (3.11), we conclude that

for arbitrary  .
.
From now on, we establish the following results on the local solvability of the following equation,

Lemma 3.2.
Let  be a solution of (HIE-1) and
be a solution of (HIE-1) and  . Then, the following inequality holds, for any
. Then, the following inequality holds, for any  ,
,

where  .
.
Proof.
We remark that from (2.11), (2.12), it follows that there is a constant  such that
such that

Consider the following equation:

Multipying on both sides of  , we get
, we get

and integrating this over  , by (1.6), (2.5), (3.18) and (Hb-1), we have
, by (1.6), (2.5), (3.18) and (Hb-1), we have

that is,

Applying Gronwall lemma, the proof of the lemma is complete.
Theorem 3.3.
Assume that  ,
,  and (Hb). Then, there exists a time
and (Hb). Then, there exists a time  such that (HIE-1) admits a unique solution
such that (HIE-1) admits a unique solution

Proof.
Assume that (2.5) holds for  . Let the constant
. Let the constant  satisfy the following inequality:
satisfy the following inequality:

Let us fix  such that
such that

where  is given by (Hb).
is given by (Hb).
Invoking Proposition 2.1, for a given  , the problem
, the problem

has a unique solution  . To prove the existence and uniqueness of solutions of semilinear type (HIE-1), by virtue of Lemma 3.2, we are going to show that the mapping defined by
. To prove the existence and uniqueness of solutions of semilinear type (HIE-1), by virtue of Lemma 3.2, we are going to show that the mapping defined by  maps is strictly contractive from
maps is strictly contractive from  into itself if the condition (3.25) is satisfied.
into itself if the condition (3.25) is satisfied.
Lemma 3.4.
Let  be the solutions of (HIE-2) with
be the solutions of (HIE-2) with  replaced by
replaced by  where
where  is the ball of radius
is the ball of radius  centered at zero of
centered at zero of  , respectively. Then the following inequality holds:
, respectively. Then the following inequality holds:

where

Proof.
Let  be the solutions of (HIE-2) with
be the solutions of (HIE-2) with  replaced by
replaced by  , respectively. Then, we have that
, respectively. Then, we have that

Multiplying on both sides of  and by (2.8), we get
and by (2.8), we get

and so, by (3.18), (2.5), (Hb), we obtain

Putting

and integrating (3.30) over  , this yields
, this yields

From (3.32) it follows that

Integrating (3.33) over  we have
we have

thus, we get

From (3.32) and (3.35) it follows that

which implies

By using Lemma 3.1, we obtain that

The proof of lemma is complete.
From (3.26) and (3.36) it follows that

Starting from the initial value  , consider a sequence
, consider a sequence  satisfying
satisfying

Then from (3.39) it follows that

So by virtue of the condition (3.25) the contraction principle gives that there exists  such that
such that

and hence, from (3.41) there exists  such that
such that

Now, we give a norm estimation of the solution (HIE) and establish the global existence of solutions with the aid of norm estimations.
Theorem 3.5.
Let the assumption (Hb) be satisfied. Assume that  and
and  for any
for any  . Then, the solution
. Then, the solution  of (HIE) exists and is unique in
of (HIE) exists and is unique in

Furthermore, there exists a constant  depending on
depending on  such that
such that

Proof.
Let  be the solution of
be the solution of

Then, since

by multiplying by  , from (Hb), (3.18) and the monotonicity of
, from (Hb), (3.18) and the monotonicity of  , we obtain
, we obtain

By integrating on (3.48) over  we have
we have

By the procedure similar to (3.39) we have

Put

Then it holds

and hence, from (2.16) in Proposition 2.1, we have that

for some positive constant  . Noting that by (Hb)
. Noting that by (Hb)

and by Proposition 2.1

it is easy to obtain the norm estimate of  in
in  satisfying (3.45).
satisfying (3.45).
Now from Theorem 3.3 it follows that

So, we can solve the equation in  and obtain an analogous estimate to (3.53). Since the condition (3.25) is independent of initial values, the solution of (HIE-1) can be extended the internal
and obtain an analogous estimate to (3.53). Since the condition (3.25) is independent of initial values, the solution of (HIE-1) can be extended the internal  for a natural number
for a natural number  , that is, for the initial
, that is, for the initial  in the interval
in the interval  , as analogous estimate (3.53) holds for the solution in
, as analogous estimate (3.53) holds for the solution in  . Furthermore, the estimate (3.45) is easily obtained from (3.53) and (3.56).
. Furthermore, the estimate (3.45) is easily obtained from (3.53) and (3.56).
We show that  is a solution of the problem (HIE). Lemma 3.4 and (Hb) give that
is a solution of the problem (HIE). Lemma 3.4 and (Hb) give that

and for  , there exists a unique solution
, there exists a unique solution  of (HIE) belonging to
of (HIE) belonging to

and satisfying (3.44).
From (3.44)and (3.57), we can extract a subsequence from  , still denoted by
, still denoted by  , such that
, such that


Here, we remark that if  is compactly embedded in
is compactly embedded in  and
and  , the following embedding
, the following embedding

is compact in view [13, Theorem 2]. Hence, the mapping

By a solution of (HIE-1), we understand a mild solution that has a form

so letting  and using the convergence results above, we obtain
and using the convergence results above, we obtain

Now, we show that  a.e. in
a.e. in  . Indeed, from (3.62) we have
. Indeed, from (3.62) we have  strongly in
strongly in  and hence
and hence  a.e. in
a.e. in  for each
for each  Let
Let  and
and  Using the theorem of Lusin and Egoroff, we can choose a subset
Using the theorem of Lusin and Egoroff, we can choose a subset  such that
such that  and
and  uniformly on
uniformly on  Thus, for each
Thus, for each  there is an
there is an  such that
such that

Then, if  we have
we have  for all
for all  and
and 
Therefore we have

Let  Then
Then

Letting  in this inequality and using (3.60), we obtain
in this inequality and using (3.60), we obtain

where  Letting
Letting  in this inequality, we deduce that
in this inequality, we deduce that

and letting  we get
we get

This implies that  a.e. in
a.e. in  This completes the proof of theorem.
This completes the proof of theorem.
Remark 3.6.
In terms of Proposition 2.1, we remark that if  and
and  for any
for any  then the solution
then the solution  of (HIE) exists and is unique in
of (HIE) exists and is unique in

Futhermore, there exists a constant  depending on
depending on  such that
such that

Theorem 3.7.
Let the assumption (Hb) be satisfied
(1)if  , then the solution
, then the solution  of (HIE) belongs to
of (HIE) belongs to  and the mapping
and the mapping

is continuous.
-
(2)
let
 . Then the solution
. Then the solution  of (HIE) belongs to
of (HIE) belongs to 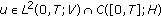 and the mapping
and the mapping 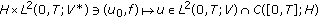 (3.74)
(3.74)
is continuous.
Proof.
-
(1)
It is easy to show that if
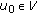 and
and  , then
, then  belongs to
belongs to 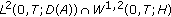 . let
. let  and
and 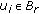 be the solution of (HIE) with
be the solution of (HIE) with 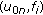 in place of
in place of  for
for 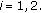 Then in view of Proposition 2.1, we have
Then in view of Proposition 2.1, we have  (3.75)
(3.75)
Since

we get

Hence, arguing as in (2.8), we get

Combining (3.75) with (3.78), we obtain

Suppose that  in
in  and let
and let  and
and  be the solutions (HIE) with
be the solutions (HIE) with  and
and  , respectively. Let
, respectively. Let  be such that
be such that

Then by virtue of (3.79) with  replaced by
replaced by  we see that
we see that

This implies that  in
in  . Hence the same argument shows that
. Hence the same argument shows that  in
in

Repeating this process we conclude that  in
in 
-
(2)
If
 then
then  belongs to
belongs to 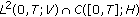 from Theorem 3.5. Let
from Theorem 3.5. Let 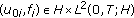 and
and 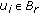 be the solution of (HIE) with
be the solution of (HIE) with 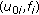 in place of
in place of 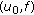 for
for 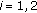 . Multiplying (HIE) by
. Multiplying (HIE) by 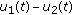 , we have
, we have  (3.83)
(3.83)
Put

Then, by the similar argument in (3.32), we get

and we have that

thus, arguing as in (3.35) we have

Combining this inequality with (3.85) it holds that

By Lemma 3.1 the following inequality

implies that

Hence, from (3.88) and (3.90) it follows that

The last term of (3.91) is estimated as

Let  be such that
be such that

Hence, from (3.91) and (3.92) it follows that there exists a constant  such that
such that

Suppose  in
in  , and let
, and let  and
and  be the solutions (HIE) with
be the solutions (HIE) with  and
and  , respectively. Then, by virtue of (3.94), we see that
, respectively. Then, by virtue of (3.94), we see that  in
in  . This implies that
. This implies that  in
in  . Therefore the same argument shows that
. Therefore the same argument shows that  in
in

Repeating this process, we conclude that  in
in  .
.
References
Miettinen M: A parabolic hemivariational inequality. Nonlinear Analysis: Theory, Methods & Applications 1996,26(4):725–734. 10.1016/0362-546X(94)00312-6
Miettinen M, Panagiotopoulos PD: On parabolic hemivariational inequalities and applications. Nonlinear Analysis: Theory, Methods & Applications 1999,35(7):885–915. 10.1016/S0362-546X(97)00720-7
Panagiotopoulos PD: Inequality Problems in Mechanics and Applications: Convex and Nonconvex Energy Functions. Birkhäuser, Boston, Mass, USA; 1985:xx+412.
Panagiotopoulos PD: Modelling of nonconvex nonsmooth energy problems. Dynamic hemivariational inequalities with impact effects. Journal of Computational and Applied Mathematics 1995,63(1–3):123–138.
Park JY, Kim HM, Park SH: On weak solutions for hyperbolic differential inclusion with discontinuous nonlinearities. Nonlinear Analysis: Theory, Methods & Applications 2003,55(1–2):103–113. 10.1016/S0362-546X(03)00216-5
Park JY, Park SH: On solutions for a hyperbolic system with differential inclusion and memory source term on the boundary. Nonlinear Analysis: Theory, Methods & Applications 2004,57(3):459–472. 10.1016/j.na.2004.02.024
Migórski S, Ochal A: Vanishing viscosity for hemivariational inequalities modeling dynamic problems in elasticity. Nonlinear Analysis: Theory, Methods & Applications 2007,66(8):1840–1852. 10.1016/j.na.2006.02.028
Rauch J: Discontinuous semilinear differential equations and multiple valued maps. Proceedings of the American Mathematical Society 1977,64(2):277–282. 10.1090/S0002-9939-1977-0442453-6
Di Blasio G, Kunisch K, Sinestrari E: -regularity for parabolic partial integro-differential equations with delay in the highest-order derivatives. Journal of Mathematical Analysis and Applications 1984,102(1):38–57. 10.1016/0022-247X(84)90200-2
Ahmed NU: Optimization and Identification of Systems Governed by Evolution Equations on Banach Space, Pitman Research Notes in Mathematics Series. Volume 184. Longman Scientific & Technical, Harlow, UK; 1988:vi+187.
Barbu V: Nonlinear Semigroups and Differential Equations in Banach Spaces. Nordhoff, Leiden, The Netherlands; 1976:352.
Brézis H: Opérateurs Maximaux Monotones et Semigroupes de Contractions dans un Espace de Hilbert. North Holland, Amsterdam, The Netherlands; 1973.
Aubin J-P: Un théorème de compacité. Comptes Rendus de l'Académie des Sciences 1963, 256: 5042–5044.
Acknowledgment
The authors wish to thank the referees for careful reading of manuscript, for valuable suggestions and many useful comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Park, DG., Jeong, JM. & Park, S.H. Regularity of Parabolic Hemivariational Inequalities with Boundary Conditions. J Inequal Appl 2009, 207873 (2009). https://doi.org/10.1155/2009/207873
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/207873
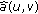 be a bounded sesquilinear form defined in
be a bounded sesquilinear form defined in  by
by 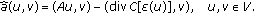
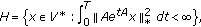
 . Then the solution
. Then the solution  of (HIE) belongs to
of (HIE) belongs to 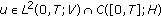 and the mapping
and the mapping 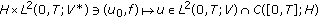
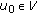 and
and  , then
, then  belongs to
belongs to 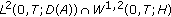 . let
. let  and
and 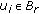 be the solution of (HIE) with
be the solution of (HIE) with 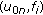 in place of
in place of  for
for 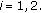 Then in view of Proposition 2.1, we have
Then in view of Proposition 2.1, we have 
 then
then  belongs to
belongs to 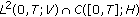 from Theorem 3.5. Let
from Theorem 3.5. Let 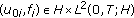 and
and 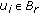 be the solution of (HIE) with
be the solution of (HIE) with 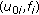 in place of
in place of 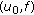 for
for 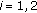 . Multiplying (HIE) by
. Multiplying (HIE) by 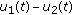 , we have
, we have 
Comments
View archived comments (1)