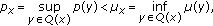- Research Article
- Open access
- Published:
Multiple Solutions for a Class of 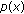 -Laplacian Systems
-Laplacian Systems
Journal of Inequalities and Applications volume 2009, Article number: 191649 (2009)
Abstract
We study the multiplicity of solutions for a class of Hamiltonian systems with the  -Laplacian. Under suitable assumptions, we obtain a sequence of solutions associated with a sequence of positive energies going toward infinity.
-Laplacian. Under suitable assumptions, we obtain a sequence of solutions associated with a sequence of positive energies going toward infinity.
1. Introduction and Main Results
Since the space  and
and  were thoroughly studied by Kováčik and Rákosník [1], variable exponent Sobolev spaces have been used in the last decades to model various phenomena. In [2], Růžička presented the mathematical theory for the application of variable exponent spaces in electro-rheological fluids.
were thoroughly studied by Kováčik and Rákosník [1], variable exponent Sobolev spaces have been used in the last decades to model various phenomena. In [2], Růžička presented the mathematical theory for the application of variable exponent spaces in electro-rheological fluids.
In recent years, the differential equations and variational problems with  -growth conditions have been studied extensively; see for example [3–6]. In [7], De Figueiredo and Ding discussed the multiple solutions for a kind of elliptic systems on a smooth bounded domain. Motivated by their work, we will consider the following sort of
-growth conditions have been studied extensively; see for example [3–6]. In [7], De Figueiredo and Ding discussed the multiple solutions for a kind of elliptic systems on a smooth bounded domain. Motivated by their work, we will consider the following sort of  -Laplacian systems with "concave and convex nonlinearity":
-Laplacian systems with "concave and convex nonlinearity":

where  is a bounded domain,
is a bounded domain,  is continuous on
is continuous on  and satisfies
and satisfies  , and
, and  is a
is a  function. In this paper, we are mainly interested in the class of Hamiltonians
function. In this paper, we are mainly interested in the class of Hamiltonians  such that
such that

where  Here we denote
Here we denote

and denote by  the fact that
the fact that  Throughout this paper,
Throughout this paper,  satisfies the following conditions:
satisfies the following conditions:
(H1)  Writing
Writing 
(H2) there exist  such that
such that

where  is positive constant;
is positive constant;
(H3) there exist  with
with  , and
, and  such that
such that

when 
As [8,Lemma 1.1], from assumption (H3), there exist  such that
such that

for any  We can also get that there exists
We can also get that there exists  such that
such that

for any  In this paper, we will prove the following result.
In this paper, we will prove the following result.
Theorem 1.1.
Assume that hypotheses (H1)–(H3) are fulfilled. If  is even in
is even in  , then problem (1.1) has a sequence of solutions
, then problem (1.1) has a sequence of solutions  such that
such that

as 
2. Preliminaries
First we recall some basic properties of variable exponent spaces  and variable exponent Sobolev spaces
and variable exponent Sobolev spaces  where
where  is a domain. For a deeper treatment on these spaces, we refer to [1, 9–11].
is a domain. For a deeper treatment on these spaces, we refer to [1, 9–11].
Let  be the set of all Lebesgue measurable functions
be the set of all Lebesgue measurable functions  and
and

The variable exponent space  is the class of all functions
is the class of all functions  such that
such that  Under the assumption that
Under the assumption that  is a Banach space equipped with the norm (2.1).
is a Banach space equipped with the norm (2.1).
The variable exponent Sobolev space  is the class of all functions
is the class of all functions  such that
such that  and it can be equipped with the norm
and it can be equipped with the norm

For  if we define
if we define

then  and
and  are equivalent norms on
are equivalent norms on 
By  we denote the subspace of
we denote the subspace of  which is the closure of
which is the closure of  with respect to the norm (2.2) and denote the dual space of
with respect to the norm (2.2) and denote the dual space of  by
by  We know that if
We know that if  is a bounded domain,
is a bounded domain,  and
and  are equivalent norms on
are equivalent norms on 
Under the condition  is a separable and reflexive Banach space, then there exist
is a separable and reflexive Banach space, then there exist  and
and  such that
such that

In the following, we will denote that  where
where

For any  define the norm
define the norm  For any
For any  set
set  and
and

denote the complement of  in
in  by
by 
3. The Proof of Theorem 1.1
Definition 3.1.
We say that  is a weak solution of problem (1.1), that is,
is a weak solution of problem (1.1), that is,

In this section, we denote that  for any
for any  , and
, and  is positive constant, for any
is positive constant, for any 
Lemma 3.2.
Any  sequence
sequence  , that is,
, that is,  and
and  as
as  is bounded.
is bounded.
Proof.
Let  be sufficiently small such that
be sufficiently small such that 



Let  be such that
be such that  as
as  We get
We get

As  by the Young inequality, we can get that for any
by the Young inequality, we can get that for any 

Let  be sufficiently small such that
be sufficiently small such that

then

Note that  by the Young inequality, for any
by the Young inequality, for any  we get
we get

Let  be sufficiently small such that
be sufficiently small such that  and
and  then we get
then we get

Note that

and for  being large enough, we have
being large enough, we have

It is easy to know that if  and
and 

thus we get

then  are bounded. Similarly, if
are bounded. Similarly, if  or
or  we can also get that
we can also get that  are bounded. It is immediate to get that
are bounded. It is immediate to get that  is bounded in
is bounded in 
Lemma 3.3.
Any  sequence contains a convergent subsequence.
sequence contains a convergent subsequence.
Proof.
Let  be a
be a  sequence. By Lemma 3.2, we obtain that
sequence. By Lemma 3.2, we obtain that  is bounded in
is bounded in  As
As  is reflexive, passing to a subsequence, still denoted by
is reflexive, passing to a subsequence, still denoted by  we may assume that there exists
we may assume that there exists  such that
such that  weakly in
weakly in  Then we can get
Then we can get  weakly in
weakly in  . Note that
. Note that

It is easy to get that

and  in
in  in
in  as
as  Then
Then

as  By condition (H2), we obtain
By condition (H2), we obtain

It is immediate to get that  are bounded and
are bounded and  then we get
then we get

as  Similar to [3, 4], we divide
Similar to [3, 4], we divide  into two parts:
into two parts:

On  we have
we have

then  On
On  we have
we have

Thus we get  Then
Then  in
in  as
as  Similarly,
Similarly,  in
in 
Lemma 3.4.
There exists  such that
such that  for all
for all  with
with 
Proof.
For any  we have
we have

In the following, we will consider 
-
(i)
If
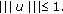 We have
We have 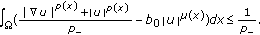 (321)
(321)
-
(ii)
If
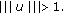 Note that
Note that 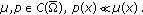 For any
For any 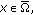 there exists
there exists 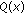 which is an open subset of
which is an open subset of  such that
such that 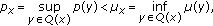 (322)
(322)
then  is an open covering of
is an open covering of  As
As  is compact, we can pick a finite subcovering
is compact, we can pick a finite subcovering  for
for  Thus there exists a sequence of open set
Thus there exists a sequence of open set  such that
such that  and
and

for  Denote that
Denote that  then we have
then we have

where  As
As  is a finite dimensional space, we have
is a finite dimensional space, we have  for
for 
We denote by  the maximum of polynomial
the maximum of polynomial  on
on  for
for  Then there exists
Then there exists  such that
such that

for  and
and  where
where 
Let  If
If  we get
we get  or
or 
(i)If  It is easy to verify that there exists at least
It is easy to verify that there exists at least  such that
such that  thus
thus

(ii)If  We obtain
We obtain

Now we get the result.
Lemma 3.5.
There exist  and
and  such that
such that  for any
for any  with
with 
Proof.
For  By condition (H2), there exists
By condition (H2), there exists  such that
such that

Let  we get
we get

Denote that

thus

Let

By [5, Lemma 3.3], we get that  as
as  then
then

when  is sufficiently large and
is sufficiently large and  It is easy to get that
It is easy to get that  as
as 
Lemma 3.6.
I is bounded from above on any bounded set of 
Proof.
For  We get
We get

By conditions (H2) and (H3), we know that if  and if
and if  Then
Then

and it is easy to get the result.
Proof.
By Lemmas 3.2–3.6 above, and [7, Proposition 2.1 and Remark 2.1], we know that the functional  has a sequence of critical values
has a sequence of critical values  as
as  Now we complete the proof.
Now we complete the proof.
References
Kováčik O, Rákosník J: On spaces and . Czechoslovak Mathematical Journal 1991,41(116)(4):592–618.
Růžička M: Electrorheological Fluids: Modeling and Mathematical Theory, Lecture Notes in Mathematics. Volume 1748. Springer, Berlin, Germany; 2000:xvi+176.
Chabrowski J, Fu Y: Existence of solutions for -Laplacian problems on a bounded domain. Journal of Mathematical Analysis and Applications 2005,306(2):604–618. 10.1016/j.jmaa.2004.10.028
Chabrowski J, Fu Y: Corrigendum to: "Existence of solutions for -Laplacian problems on a bounded domain". Journal of Mathematical Analysis and Applications 2006,323(2):1483. 10.1016/j.jmaa.2005.11.036
Fan X, Han X: Existence and multiplicity of solutions for -Laplacian equations in . Nonlinear Analysis: Theory, Methods & Applications 2004,59(1–2):173–188.
Mihăilescu M, Rădulescu V: A multiplicity result for a nonlinear degenerate problem arising in the theory of electrorheological fluids. Proceedings of the Royal Society of London. Series A 2006,462(2073):2625–2641. 10.1098/rspa.2005.1633
De Figueiredo DG, Ding YH: Strongly indefinite functionals and multiple solutions of elliptic systems. Transactions of the American Mathematical Society 2003,355(7):2973–2989. 10.1090/S0002-9947-03-03257-4
Felmer PL: Periodic solutions of "superquadratic" Hamiltonian systems. Journal of Differential Equations 1993,102(1):188–207. 10.1006/jdeq.1993.1027
Edmunds DE, Lang J, Nekvinda A: On norms. Proceedings of the Royal Society of London. Series A 1999,455(1981):219–225. 10.1098/rspa.1999.0309
Edmunds DE, Rákosník J: Sobolev embeddings with variable exponent. Studia Mathematica 2000,143(3):267–293.
Fan X, Zhao Y, Zhao D: Compact imbedding theorems with symmetry of Strauss-Lions type for the space . Journal of Mathematical Analysis and Applications 2001,255(1):333–348. 10.1006/jmaa.2000.7266
Acknowledgments
This work is supported by Science Research Foundation in Harbin Institute of Technology (HITC200702) and The Natural Science Foundation of Heilongjiang Province (A2007-04).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Fu, Y., Zhang, X. Multiple Solutions for a Class of 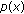 -Laplacian Systems.
J Inequal Appl 2009, 191649 (2009). https://doi.org/10.1155/2009/191649
-Laplacian Systems.
J Inequal Appl 2009, 191649 (2009). https://doi.org/10.1155/2009/191649
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/191649
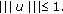 We have
We have 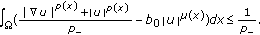
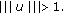 Note that
Note that 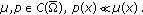 For any
For any 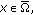 there exists
there exists 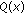 which is an open subset of
which is an open subset of  such that
such that