- Research Article
- Open access
- Published:
Endpoint Estimates for a Class of Littlewood-Paley Operators with Nondoubling Measures
Journal of Inequalities and Applications volume 2009, Article number: 175230 (2009)
Abstract
Let  be a positive Radon measure on
be a positive Radon measure on  which may be nondoubling. The only condition that
which may be nondoubling. The only condition that  satisfies is
satisfies is 
 for all
for all  ,
,  , and some fixed constant
, and some fixed constant  . In this paper, we introduce the operator
. In this paper, we introduce the operator  related to such a measure and assume it is bounded on
related to such a measure and assume it is bounded on  . We then establish its boundedness, respectively, from the Lebesgue space
. We then establish its boundedness, respectively, from the Lebesgue space  to the weak Lebesgue space
to the weak Lebesgue space  , from the Hardy space
, from the Hardy space  to
to  and from the Lesesgue space
and from the Lesesgue space  to the space
to the space  . As a corollary, we obtain the boundedness of
. As a corollary, we obtain the boundedness of  in the Lebesgue space
in the Lebesgue space  with
with  .
.
1. Introduction
A positive Radon measure  on
on  is said to be doubling if there exists some constant
is said to be doubling if there exists some constant  such that
such that  for all
for all  ,
,  . It is well known that the doubling condition is an essential assumption in many results of classical Calderón-Zygmund theory. However in the recent years, it has been shown that a big part of the classical theory remains valid if the doubling assumption on
. It is well known that the doubling condition is an essential assumption in many results of classical Calderón-Zygmund theory. However in the recent years, it has been shown that a big part of the classical theory remains valid if the doubling assumption on  is substituted by the growth condition as follows:
is substituted by the growth condition as follows:

for all  , where
, where  is some fixed number with
is some fixed number with  . For example, In 2001, Tolsa in [1, 2] investigated the weak (1,1) inequality for singular integrals, the Littlewood-Paley theory and the
. For example, In 2001, Tolsa in [1, 2] investigated the weak (1,1) inequality for singular integrals, the Littlewood-Paley theory and the  theorem with nondoubling measures. In 2002, García-Cuerva and Gatto [3] investigated the boundedness properties of fractional integral operators associated to nondoubling measures. In 2005, Hu et al. [4] studied the multilinear commutators of singular integrals with nondoubling measures. Since 2007, Hu et al. [5] have proved some boundedness results of Marcinkiewicz integrals with nondoubling measures on some function spaces.
theorem with nondoubling measures. In 2002, García-Cuerva and Gatto [3] investigated the boundedness properties of fractional integral operators associated to nondoubling measures. In 2005, Hu et al. [4] studied the multilinear commutators of singular integrals with nondoubling measures. Since 2007, Hu et al. [5] have proved some boundedness results of Marcinkiewicz integrals with nondoubling measures on some function spaces.
On the other hand, let  be a function on
be a function on  such that there exist positive constants
such that there exist positive constants  ,
,  ,
,  , and
, and  satisfying
satisfying
(a) and
and  ,
,
(b) ,
,
(c) for
for  .
.
For this  , we define the Littlewood-Paley's
, we define the Littlewood-Paley's  -function with nondoubling measures as follows:
-function with nondoubling measures as follows:

where  and
and  .
.
Note that if we replace  by
by  in the above definition and when
in the above definition and when  is the Poisson kernel, we obtain classical
is the Poisson kernel, we obtain classical  -function defined and studied by Stein [6] and later by Fefferman [7], where the weak (1,1) with
-function defined and studied by Stein [6] and later by Fefferman [7], where the weak (1,1) with  and weak
and weak  with
with  boundedness of
boundedness of  function were obtained. In the same paper, Fefferman [7] also established the
function were obtained. In the same paper, Fefferman [7] also established the  bounds of
bounds of  for
for  and
and  . For the more generalized
. For the more generalized  -function defined by (1.1), the
-function defined by (1.1), the  boundedness is also well known (see, e.g., [8, pages 309–318]). On the other hand, inspired by the works of Sakamoto and Yabuta in 1999, the first author in this paper studied parametric
boundedness is also well known (see, e.g., [8, pages 309–318]). On the other hand, inspired by the works of Sakamoto and Yabuta in 1999, the first author in this paper studied parametric  -function systematically in his PhD thesis [9]. Later, in 2008, Lin and Meng [10] gave some results on parametric
-function systematically in his PhD thesis [9]. Later, in 2008, Lin and Meng [10] gave some results on parametric  -function with nondoubling measures. But their result only valid for
-function with nondoubling measures. But their result only valid for  , one cannot obtain the results for classical operators even for
, one cannot obtain the results for classical operators even for  or in the classical case studied by Stein in 1961 [6].
or in the classical case studied by Stein in 1961 [6].
In this paper, we will study the properties of operator  with nondoubling measures on some function spaces under the conditions (a)–(c).
with nondoubling measures on some function spaces under the conditions (a)–(c).
First, before stating our main results, we give some notation and definitions, let  be a closed cube with sides parallel to the axes. Denote its side length by
be a closed cube with sides parallel to the axes. Denote its side length by  and its center by
and its center by  . Given
. Given  and
and  , we say
, we say  is
is  -doubling if
-doubling if  , where
, where  is the cube concentric with
is the cube concentric with  with side length
with side length  . If
. If  are not specified, by a doubling cube we mean a
are not specified, by a doubling cube we mean a  -doubling cube. For any cube
-doubling cube. For any cube  , we denote by
, we denote by  the smallest doubling cube which contains
the smallest doubling cube which contains  and has the same center as
and has the same center as  .
.
Given two cubes  in
in  , set
, set

where  is the first integer
is the first integer  such that
such that  and
and

with  , where
, where  is the first integer
is the first integer  such that
such that  .
.
In the article of [1, page 95], we know that  with constants that may depend on
with constants that may depend on  and
and  . The following atomic Hardy space
. The following atomic Hardy space  was introduced by Tolsa in [11].
was introduced by Tolsa in [11].
Definition 1.1.
For a fixed  , a function
, a function  is called an atomic block if
is called an atomic block if
(1)there exists some cube  such that
such that  ;
;
(2) ;
;
(3)there are fucntions  with supports in cubes
with supports in cubes  and numbers
and numbers  such that
such that

Define

We say that  if there are atomic blocks
if there are atomic blocks  such that
such that  with
with  . The
. The  norm of
norm of  is defined by
is defined by

where the infimum is taken over all the possible decompositions of  in atomic blocks.
in atomic blocks.
It was shown by Tolsa that the space  was proved to be the Hardy space
was proved to be the Hardy space  in [11] with equivalent norms. We will denote the space
in [11] with equivalent norms. We will denote the space  and the norm
and the norm  , respectively, by
, respectively, by  and
and  for convenience. He also proved that the dual space of
for convenience. He also proved that the dual space of  is the following space
is the following space  .
.
Definition 1.2.
Let  be a fixed constant. A function
be a fixed constant. A function  is said to be in the space
is said to be in the space  if there exists some constant
if there exists some constant  such that for any cube
such that for any cube  centered at some point of
centered at some point of 

and for any two doubling cubes 

where  denotes the mean value of
denotes the mean value of  over cube
over cube  . The minimal constant
. The minimal constant  above is defined to be the norm of
above is defined to be the norm of  in the space
in the space  and denoted by
and denoted by  .
.
Tolsa in [11] proved that the definition of the space  and
and  are independent of the choice of
are independent of the choice of  . The following space
. The following space  was introduced in [12]. It is easy to see that
was introduced in [12]. It is easy to see that  .
.
Definition 1.3.
A function  is said to be in the space
is said to be in the space  if there exists some positive constant
if there exists some positive constant  such that for any
such that for any  doubling cube
doubling cube  ,
,

and for any two  -doubling cubes
-doubling cubes  ,
,

The minimal constant  as above is defined to be the norm of
as above is defined to be the norm of  in the space
in the space  , we denote it by
, we denote it by  .
.
In this paper, we always assume that  and
and  are considered as they are defined at the beginning of this paper. Our main results are as follows.
are considered as they are defined at the beginning of this paper. Our main results are as follows.
Theorem 1.4.
Let  be a function on
be a function on  , satisfying (a)–(c),
, satisfying (a)–(c),  ,
,  . If
. If  is bounded on
is bounded on  , then it is also bounded from
, then it is also bounded from  to
to  .
.
Theorem 1.5.
Let  be a function on
be a function on  , satisfying (a)–(c),
, satisfying (a)–(c),  ,
,  . If
. If  is bounded on
is bounded on  , then it is also bounded from
, then it is also bounded from  to
to  .
.
Theorem 1.6.
Let  be a function on
be a function on  , satisfying (a)–(c),
, satisfying (a)–(c),  ,
,  . If
. If  is bounded on
is bounded on  , then for
, then for  ,
,  is either infinite everywhere or finite almost everywhere. More precisely, if
is either infinite everywhere or finite almost everywhere. More precisely, if  is finite at some point
is finite at some point  , then
, then  is
is  -finite almost everywhere and
-finite almost everywhere and

Corollary 1.7.
Let  be a function on
be a function on  , satisfying (a)–(c),
, satisfying (a)–(c),  ,
,  . If
. If  is bounded on
is bounded on  , then it is also bounded on
, then it is also bounded on  for any
for any  .
.
Remark 1.8.
It is natural to consider the similar problems with more general rough kernels. However, even in the doubling measure case, if we take  in (1.1) (in this case,
in (1.1) (in this case,  is defined and studied by [13]), from the results in [8], we know that it is impossible to give similar results as above for Littlewood-Paley
is defined and studied by [13]), from the results in [8], we know that it is impossible to give similar results as above for Littlewood-Paley  function even
function even  for
for  . In fact, by the counter example in [13], even the
. In fact, by the counter example in [13], even the  boundedness does not hold. In this sense, the condition we assumed on
boundedness does not hold. In this sense, the condition we assumed on  is necessary and reasonable. On the other hand, in 2008, Lin and Meng [10] gave some results on parametric
is necessary and reasonable. On the other hand, in 2008, Lin and Meng [10] gave some results on parametric  -function with nondoubling measures. In fact the results in [10] are only valid for
-function with nondoubling measures. In fact the results in [10] are only valid for  . By the same reason as above, one cannot obtain the result when
. By the same reason as above, one cannot obtain the result when  which in this case, the operator coincides with the classical operator studied by Torchinsky and Wang in [13] and it is a generalization of the classical operators studied by Stein and Fefferman.
which in this case, the operator coincides with the classical operator studied by Torchinsky and Wang in [13] and it is a generalization of the classical operators studied by Stein and Fefferman.
Remark 1.9.
Even in the classical case, the index  is sharp for weak
is sharp for weak  boundedness; see [6] for detail.
boundedness; see [6] for detail.
We arrange our paper as follows, in Section 2, we give and prove some key lemmas. The proof of our main theorems will be given in Section 3. Throughout this paper, the letter  will denote a positive constant that may vary at each occurrence but is independent of the essential variables.
will denote a positive constant that may vary at each occurrence but is independent of the essential variables.  will always denote that there exists a constant
will always denote that there exists a constant  , such that
, such that  .
.
2. Main Lemmas
We need two lemmas given by Tolsa.
Lemma 2.1 (see [11]).
If  are concentric cubes such that there are no
are concentric cubes such that there are no  -doubling cubes with
-doubling cubes with  of the form
of the form  ,
,  , with
, with  , then
, then

where  depends only on
depends only on  ,
,  ,
,  ,
,  .
.
Lemma 2.2 (see [11]).
For any  and any
and any  then we have one has the following:
then we have one has the following:
(a)there exists a family of almost disjoint cubes  (that means
(that means  ,
,  depends only on
depends only on  ) such that
) such that
(a.1) ;
;
(a.2) for any
for any  ;
;
(a.3) a.e.
a.e.  on
on  ,
,
(b)for each  , let
, let  be the smallest (
be the smallest ( )-doubling cube of the form
)-doubling cube of the form  ,
,  , with that
, with that  , and let
, and let  , then there exists a family of functions
, then there exists a family of functions  with
with  and with constant sign satisfying
and with constant sign satisfying
(b.1) ;
;
(b.2) , where
, where  is some constant;
is some constant;
(b.3) .
.
To prove our theorems, we prepare another two key lemmas.
For any subset  , we denote
, we denote

It is easy to see that

Lemma 2.3.
Let  and
and  be the same as in Lemma 2.2, and let
be the same as in Lemma 2.2, and let  be
be  center. Then for any
center. Then for any  and
and  ,
,

Lemma 2.4.
Let  and
and  be the same as in Lemma 2.2, and let
be the same as in Lemma 2.2, and let  be
be  center. For any
center. For any  and
and  , then
, then

Proof of Lemma 2.3.
Denote

Set

It is easy to see

We first estimate  . Set
. Set

We have

Note that  and
and  , then
, then  ,
,  . These two inequalities will always be used in the following proof, so we will not mention them every time.
. These two inequalities will always be used in the following proof, so we will not mention them every time.
For any  , we have that
, we have that  ,
,  ,
,  ,
,  ,
,  . Then
. Then

For any  , we get
, we get  . Then
. Then

For  , we obtain that
, we obtain that  ,
,  . Therefore
. Therefore

For  , we have that
, we have that  ,
,  . Therefore
. Therefore

Thus, we get

Next we estimate  . Set
. Set

For any  , there exist two constants
, there exist two constants  ,
,  such that
such that  . Since
. Since  ,
,  , we then have that
, we then have that

For any  , the following inequalities hold:
, the following inequalities hold:  ,
,  , and
, and  . It follows that
. It follows that

Next we estimate  . Set
. Set

Then

For any  , we can get that
, we can get that  and there exist two constants
and there exist two constants  and
and  such that
such that  . Then
. Then

For any  , we can get
, we can get  and
and  . Then
. Then

Next we estimate  . Set
. Set

If  , we obtain
, we obtain  ,
,  and
and

Therefore

If  , we have
, we have  and
and

Therefore

If  , we have
, we have  and
and  . Then
. Then

The proof of Lemma 2.3 is finished.
Proof of Lemma 2.4.
Denote

Let  and divide
and divide  into four parts
into four parts

Then  .
.
Since  and
and  , we have that
, we have that  ,
,  .
.
We first estimate  . Set
. Set

Then

For any  , we have that
, we have that  and
and  . Then we get
. Then we get

and therefore

For any  , we have
, we have  ,
,  . It follows that
. It follows that

If  , we will get
, we will get  . It follows that
. It follows that

If  , we obtain that
, we obtain that  . Thus we can get
. Thus we can get

Next we estimate  . Set
. Set

Then

For any  , the inequalities
, the inequalities  and
and  hold, and we have
hold, and we have

For any  , the inequalities
, the inequalities  and
and  hold, and we can get
hold, and we can get

Next we estimate  . Let
. Let

Then

Since  , we can choose
, we can choose  small enough such that
small enough such that  and
and  .
.
Now denote

and for a subset  , we denote
, we denote

It is easy to see that  .
.
For any  , we have
, we have  ,
,  . It follows that
. It follows that

The last inequality holds because  and we choose
and we choose  small enough such that
small enough such that  , and then we can get
, and then we can get  , which leads to the above inequality. Using these inequalities, we obtain
, which leads to the above inequality. Using these inequalities, we obtain

If  , we get
, we get  . It follows that
. It follows that

Next we estimate  . Set
. Set

Then

For any  , we have
, we have  . Then we get
. Then we get

If  , we get
, we get  and
and  . Then we can obtain
. Then we can obtain

If  , we get
, we get  . Then
. Then

For any  , the inequalities
, the inequalities  ,
,  and
and  hold, from which we obtain
hold, from which we obtain

If  , we have
, we have  . Then
. Then

If  , we have
, we have  and it follows that
and it follows that

If  , we get
, we get  and
and  . Then we have
. Then we have

3. Proof of Theorems
Proof of Theorem 1.4.
To prove Theorem 1.4, we will choose  and
and  .
.
Let  and
and  . Applying Lemma 2.2 to
. Applying Lemma 2.2 to  and
and  , we obtain a family of almost disjoint cubes
, we obtain a family of almost disjoint cubes  . With the notation
. With the notation  ,
,  ,
,  the same as in Lemma 2.2, we can decompose
the same as in Lemma 2.2, we can decompose  , with that
, with that  and
and  . And
. And  can be decomposed as
can be decomposed as  . By (a.1) of Lemma 2.2, we have
. By (a.1) of Lemma 2.2, we have  .
.
Thus, to prove that  is of weak type
is of weak type  , we only need to prove
, we only need to prove

Since  and
and  , we only need to show that both
, we only need to show that both  and
and  satisfy the inequality (2.4).
satisfy the inequality (2.4).
For  , it follows from (b.1) of Lemma 2.2 that
, it follows from (b.1) of Lemma 2.2 that  , and we have
, and we have  . Using
. Using  -boundedness of
-boundedness of and (a.3) and (b.2) from Lemma 2.2, we obtain
and (a.3) and (b.2) from Lemma 2.2, we obtain

To prove that  satisfies inequality (3.1), it suffices to show that
satisfies inequality (3.1), it suffices to show that

Since  , we have that
, we have that

If we can prove

then we finish the proof of Theorem 1.4.
We first estimate  and divide it into two parts
and divide it into two parts

By the assumption of  boundedness of
boundedness of  , and the fact that
, and the fact that  is the
is the  doubling cube, it is easy to see that
doubling cube, it is easy to see that

Next we estimate  . By the Minkowski's inequality, Fubini's theorem and condition (b) of
. By the Minkowski's inequality, Fubini's theorem and condition (b) of  that
that  , we have the following estimate:
, we have the following estimate:

Choose  small enough such that
small enough such that  ,
,  and
and  .
.
For any subset  , we denote
, we denote

Let  be
be  center. Using the above notations, it is easy to see that
center. Using the above notations, it is easy to see that

By Lemma 2.3, we will have the following inequalities:


where we used Lemma 2.1 to estimate

We now estimate  . Let
. Let  . Recall that
. Recall that  , and
, and

We first estimate  . By the Minkowski's inequality, Fubini's theorem and property (b) of
. By the Minkowski's inequality, Fubini's theorem and property (b) of  , we can obtain that
, we can obtain that

If we prove

for any  and
and  , then
, then

and by Lemma 2.2, we conclude that  .
.
Now choose  small enough such that
small enough such that  ,
,  and
and  . Then for any
. Then for any  and
and  , note that
, note that 

Next we estimate  . By property (c) of
. By property (c) of  and
and  , we have
, we have

since  . Using the above inequality, Minkowski's inequality and Fubini's theorem, we get
. Using the above inequality, Minkowski's inequality and Fubini's theorem, we get

So by Lemma 2.4, for  and any
and any 

Then we get

and we will have  . With the estimates of
. With the estimates of

we obtain that

Thus,

Therefore we finish the proof of Theorem 1.4.
Proof of Theorem 1.5.
Note that the definition of  is independent of the choice of the constant
is independent of the choice of the constant  , we can assume that
, we can assume that  , still with
, still with  . By Theorem 1.4, the operator
. By Theorem 1.4, the operator  is bounded from
is bounded from  to
to  . By a standard argument, we only need to prove that
. By a standard argument, we only need to prove that  for any atomic block
for any atomic block  with supp
with supp Write
Write

By definition of  , we have
, we have  . By (3.25) in the proof of Theorem 1.4, we can get
. By (3.25) in the proof of Theorem 1.4, we can get

To estimate  , let
, let  be as in Definition 1.1 and write
be as in Definition 1.1 and write

By the assumption of  boundedness of
boundedness of  and the Holder inequality,
and the Holder inequality,

By (3.11) in the proof of Theorem 1.4,


where  is a cube and has the same center as
is a cube and has the same center as  and
and  ,
,  is the center of
is the center of  . From (3.29) to (3.30), we use the conclusion
. From (3.29) to (3.30), we use the conclusion

As a matter of fact, let  and then by the definition of
and then by the definition of  , we get that
, we get that

Using (3.30) and the fact that

we have

From (3.29) and (3.35), we can obtain that

We have

Combining (3.27) and (3.37), we finish the proof of Theorem 1.5.
Proof of Theorem 1.6.
Now we begin to prove Theorem 1.6. First we claim that there is a positive constant  such that for any
such that for any  and
and  -doubling cube
-doubling cube  , the following inequality holds:
, the following inequality holds:

To prove (3.38), for each fixed cube  , let
, let  be the smallest ball which contains
be the smallest ball which contains  and has the same center as
and has the same center as  . Then
. Then  . We decompose
. We decompose  as
as

By the Hölder's inequality and  boundedness of
boundedness of  , we have
, we have

We denote by  the radius of
the radius of  . Note that
. Note that  for any
for any  and for any
and for any  , then by Minkowski's inequality, we have
, then by Minkowski's inequality, we have

Since we have the following estimate:

We claim

Then

By (3.42), (3.44), and (3.45), we can obtain

The method to prove (3.43) is quite similar as to prove (2.4) in the proof of Theorem 1.4 and we omit it.
Thus, to prove (3.38), we only need to prove for any  , the following inequality holds:
, the following inequality holds:

We note that  can be looked as a vector valued Calderón-Zygmund singular integral operator in the following Hilbert space
can be looked as a vector valued Calderón-Zygmund singular integral operator in the following Hilbert space  :
:

In fact,  can be written by
can be written by

where  . Also note that for
. Also note that for  ,
,

where  . We will divide
. We will divide  into four parts, namely,
into four parts, namely,

Then

This can be obtained from the same idea used before, see also the main step in [14], here we omit the proof of it.
From (3.38), we get that for  , if
, if  for some point
for some point  , then
, then  is
is  -finite almost everywhere and in this case we have
-finite almost everywhere and in this case we have

provided that  is a
is a  -doubling cube.
-doubling cube.
To prove  , we still need to prove that
, we still need to prove that  satisfies
satisfies

for any two  -doubling cubes
-doubling cubes  .
.
Let  and set
and set  , then
, then

Again, we can get the conclusion under the nondoubling condition which is similar to the proof of (2.2) in [14] that

For any  and each fixed
and each fixed  , similar to the proof of (2.4) from Lemma 2.3, we have that
, similar to the proof of (2.4) from Lemma 2.3, we have that

Therefore we have

Next we estimate  . By an estimate similar to (3.45), we have
. By an estimate similar to (3.45), we have

By (3.54), (3.55), (3.57), and (3.58), we can get that

Take mean value over  for
for  and over
and over  for
for  , we get
, we get

Therefore

Since by Hölder's inequality, the  boundedness assumption of
boundedness assumption of  and the fact that
and the fact that  is
is  -doubling, we have that
-doubling, we have that

which completes the proof of Theorem 1.6.
Using Theorems 1.4 and 1.5 and [4, Theorem 3.1], Corollary 1.7 is obvious.
References
Tolsa X: A proof of the weak
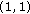 inequality for singular integrals with non doubling measures based on a Calderón-Zygmund decomposition. Publicacions Matemàtiques 2001,45(1):163–174.
inequality for singular integrals with non doubling measures based on a Calderón-Zygmund decomposition. Publicacions Matemàtiques 2001,45(1):163–174.Tolsa X: Littlewood-Paley theory and the
 theorem with non-doubling measures. Advances in Mathematics 2001,164(1):57–116. 10.1006/aima.2001.2011
theorem with non-doubling measures. Advances in Mathematics 2001,164(1):57–116. 10.1006/aima.2001.2011García-Cuerva J, Gatto AE: Boundedness properties of fractional integral operators associated to non-doubling measures. Publicacions Matemàtiques 2002,46(2):405–434.
Hu G, Meng Y, Yang D: Multilinear commutators of singular integrals with non doubling measures. Integral Equations and Operator Theory 2005,51(2):235–255. 10.1007/s00020-003-1251-y
Hu G, Lin H, Yang D: Marcinkiewicz integrals with non-doubling measures. Integral Equations and Operator Theory 2007,58(2):205–238. 10.1007/s00020-007-1481-5
Stein EM: On some funcions of Littlewood-Paley and Zygmund. Bulletin of the American Mathematical Society 1961, 67: 99–101. 10.1090/S0002-9904-1961-10515-6
Fefferman C: Inequalities for strongly singular convolution operators. Acta Mathematica 1970, 124: 9–36. 10.1007/BF02394567
Torchinsky A: Real-Variable Methods in Harmonic Analysis, Pure and Applied Mathematics. Volume 123. Academic Press, Orlando, Fla, USA; 1986:xii+462.
Xue Q: Parametric Littlewood-Paley operators, Ph.D. thesis. Beijing Normal University; 2004.
Lin H, Meng Y: Boundedness of parametrized Littlewood-Paley operators with nondoubling measures. Journal of Inequalities and Applications 2008, 2008:-25.
Tolsa X: BMO,
 , and Calderón-Zygmund operators for non doubling measures. Mathematische Annalen 2001,319(1):89–149. 10.1007/PL00004432
, and Calderón-Zygmund operators for non doubling measures. Mathematische Annalen 2001,319(1):89–149. 10.1007/PL00004432Jiang Y: Spaces of type BLO for non-doubling measures. Proceedings of the American Mathematical Society 2005,133(7):2101–2107. 10.1090/S0002-9939-05-07795-6
Torchinsky A, Wang SL: A note on the Marcinkiewicz integral. Colloquium Mathematicum 1990,60–61(1):235–243.
Xue Q, Ding Y: Weighted estimates for the multilinear commutators of the Littlewood-Paley operators. Science in China. Series A 2009,52(9):1849–1868. 10.1007/s11425-009-0049-z
Acknowledgment
The first author was supported partly by NSFC (Grant: 10701010), NSFC (Key program Grant: 10931001), CPDRFSFP (Grant: 200902070) and SRF for ROCS, SEM.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xue, Q., Zhang, J. Endpoint Estimates for a Class of Littlewood-Paley Operators with Nondoubling Measures. J Inequal Appl 2009, 175230 (2009). https://doi.org/10.1155/2009/175230
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/175230
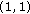 inequality for singular integrals with non doubling measures based on a Calderón-Zygmund decomposition. Publicacions Matemàtiques 2001,45(1):163–174.
inequality for singular integrals with non doubling measures based on a Calderón-Zygmund decomposition. Publicacions Matemàtiques 2001,45(1):163–174. theorem with non-doubling measures. Advances in Mathematics 2001,164(1):57–116. 10.1006/aima.2001.2011
theorem with non-doubling measures. Advances in Mathematics 2001,164(1):57–116. 10.1006/aima.2001.2011 , and Calderón-Zygmund operators for non doubling measures. Mathematische Annalen 2001,319(1):89–149. 10.1007/PL00004432
, and Calderón-Zygmund operators for non doubling measures. Mathematische Annalen 2001,319(1):89–149. 10.1007/PL00004432