- Research Article
- Open access
- Published:
Strong Convergence of an Iterative Method for Inverse Strongly Accretive Operators
Journal of Inequalities and Applications volume 2008, Article number: 420989 (2008)
Abstract
We study the strong convergence of an iterative method for inverse strongly accretive operators in the framework of Banach spaces. Our results improve and extend the corresponding results announced by many others.
1. Introduction and Preliminaries
Let  be a real Hilbert space with norm
be a real Hilbert space with norm  and inner product
and inner product  ,
,  a nonempty closed convex subset of
a nonempty closed convex subset of  and
and  a monotone operator of
a monotone operator of  into
into  . The classical variational inequality problem is formulated as finding a point
. The classical variational inequality problem is formulated as finding a point  such that
such that

for all  . Such a point
. Such a point  is called a solution of the variational inequality (1.1). Next, the set of solutions of the variational inequality (1.1) is denoted by
is called a solution of the variational inequality (1.1). Next, the set of solutions of the variational inequality (1.1) is denoted by  . In the case when
. In the case when  ,
,  holds, where
holds, where

Recall that an operator  of
of  into
into  is said to be inverse strongly monotone if there exists a positive real number
is said to be inverse strongly monotone if there exists a positive real number  such that
such that

for all  (see [1–4]). For such a case,
(see [1–4]). For such a case,  is said to be
is said to be  -inverse strongly monotone.
-inverse strongly monotone.
Recall that  is nonexpansive if
is nonexpansive if

for all  It is known that if
It is known that if  is a nonexpansive mapping of
is a nonexpansive mapping of  into itself, then
into itself, then  is
is  -inverse strongly monotone and
-inverse strongly monotone and  , where
, where  denotes the set of fixed points of
denotes the set of fixed points of  .
.
Let  be the projection of
be the projection of  onto the convex subset
onto the convex subset  . It is known that projection operator
. It is known that projection operator  is nonexpansive. It is also known that
is nonexpansive. It is also known that  satisfies
satisfies

for  Moreover,
Moreover,  is characterized by the properties
is characterized by the properties  and
and  for all
for all 
One can see that the variational inequality problem (1.1) is equivalent to some fixed-point problem. The element  is a solution of the variational inequality (1.1) if and only if
is a solution of the variational inequality (1.1) if and only if  satisfies the relation
satisfies the relation  where
where  is a constant.
is a constant.
To find a solution of the variational inequality for an inverse strongly monotone operator, Iiduka et al. [2] proved the following weak convergence theorem.
Theorem 1.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  and let
and let  be an
be an  -inverse strongly monotone operator of
-inverse strongly monotone operator of  into
into  with
with  . Let
. Let  be a sequence defined as follows:
be a sequence defined as follows:

for all  , where
, where  is the metric projection from
is the metric projection from  onto
onto  ,
,  is a sequence in
is a sequence in  and
and  is a sequence in
is a sequence in  . If
. If  and
and  are chosen so that
are chosen so that  for some
for some 
 with
with  and
and  for some
for some 
 with
with  , then the sequence
, then the sequence  defined by (1.6) converges weakly to some element of
defined by (1.6) converges weakly to some element of  .
.
Next, we assume that  is a nonempty closed and convex subset of a Banach space
is a nonempty closed and convex subset of a Banach space  . Let
. Let  be the dual space of
be the dual space of  and let
and let  denote the pairing between
denote the pairing between  and
and  . For
. For  , the generalized duality mapping
, the generalized duality mapping  is defined by
is defined by

for all  . In particular,
. In particular,  is called the normalized duality mapping. It is known that
is called the normalized duality mapping. It is known that  for all
for all  . If
. If  is a Hilbert space, then
is a Hilbert space, then  . Further, we have the following properties of the generalized duality mapping
. Further, we have the following properties of the generalized duality mapping  :
:
-
(1)
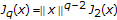
for all
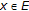 with
with 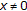 ;
; -
(2)

for all
 and
and 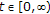 ;
; -
(3)
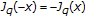
for all
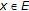 .
.
Let  . A Banach space
. A Banach space  is said to be uniformly convex if, for any
is said to be uniformly convex if, for any  , there exists
, there exists  such that, for any
such that, for any  ,
,

It is known that a uniformly convex Banach space is reflexive and strictly convex. A Banach space  is said to be smooth if the limit
is said to be smooth if the limit

exists for all  . It is also said to be uniformly smooth if the limit (1.9) is attained uniformly for
. It is also said to be uniformly smooth if the limit (1.9) is attained uniformly for  . The norm of
. The norm of  is said to be Fréchet differentiable if, for any
is said to be Fréchet differentiable if, for any  , the limit (1.9) is attained uniformly for all
, the limit (1.9) is attained uniformly for all  . The modulus of smoothness of
. The modulus of smoothness of  is defined by
is defined by

where  is a function. It is known that
is a function. It is known that  is uniformly smooth if and only if
is uniformly smooth if and only if  . Let
. Let  be a fixed real number with
be a fixed real number with  . A Banach space
. A Banach space  is said to be
is said to be  -uniformly smooth if there exists a constant
-uniformly smooth if there exists a constant  such that
such that  for all
for all  .
.
Note that
-
(1)

is a uniformly smooth Banach space if and only if
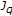 is single-valued and uniformly continuous on any bounded subset of
is single-valued and uniformly continuous on any bounded subset of  ;
; -
(2)
all Hilbert spaces,
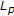 (or
(or  ) spaces (
) spaces (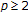 ), and the Sobolev spaces,
), and the Sobolev spaces,  (
(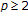 ), are
), are  -uniformly smooth, while
-uniformly smooth, while 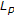 (or
(or 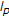 ) and
) and 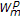 spaces (
spaces (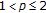 ) are
) are  -uniformly smooth.
-uniformly smooth.
Recall that an operator  of
of  into
into  is said to be accretive if there exists
is said to be accretive if there exists  such that
such that

for all  .
.
For  recall that an operator
recall that an operator  of
of  into
into  is said to be
is said to be  -inverse strongly accretive if
-inverse strongly accretive if

for all  . Evidently, the definition of the inverse strongly accretive operator is based on that of the inverse strongly monotone operator.
. Evidently, the definition of the inverse strongly accretive operator is based on that of the inverse strongly monotone operator.
Let  be a subset of
be a subset of  and let
and let  be a mapping of
be a mapping of  into
into  . Then
. Then  is said to be sunny if
is said to be sunny if

whenever  for
for  and
and  . A mapping
. A mapping  of
of  into itself is called a retraction if
into itself is called a retraction if  . If a mapping
. If a mapping  of
of  into itself is a retraction, then
into itself is a retraction, then  for all
for all  , where
, where  is the range of
is the range of  . A subset
. A subset  of
of  is called a sunny nonexpansive retract of
is called a sunny nonexpansive retract of  if there exists a sunny nonexpansive retraction from
if there exists a sunny nonexpansive retraction from  onto
onto  . We know the following lemma concerning sunny nonexpansive retraction.
. We know the following lemma concerning sunny nonexpansive retraction.
Lemma 1.1 (see [5]).
Let  be a closed convex subset of a smooth Banach space
be a closed convex subset of a smooth Banach space  , let
, let  be a nonempty subset of
be a nonempty subset of  , and let
, and let  be a retraction from
be a retraction from  onto
onto  . Then
. Then  is sunny and nonexpansive if and only if
is sunny and nonexpansive if and only if

for all  and
and  .
.
Recently, Aoyama et al. [6] first considered the following generalized variational inequality problem in a smooth Banach space. Let  be an accretive operator of
be an accretive operator of  into
into  . Find a point
. Find a point  such that
such that

for all  . In order to find a solution of the variational inequality (1.15), the authors proved the following theorem in the framework of Banach spaces.
. In order to find a solution of the variational inequality (1.15), the authors proved the following theorem in the framework of Banach spaces.
Theorem 1.
Let  be a uniformly convex and
be a uniformly convex and  -uniformly smooth Banach space and
-uniformly smooth Banach space and  a nonempty closed convex subset of
a nonempty closed convex subset of  . Let
. Let  be a sunny nonexpansive retraction from
be a sunny nonexpansive retraction from  onto
onto  ,
,  and
and  an
an  -inverse strongly accretive operator of
-inverse strongly accretive operator of  into
into  with
with  , where
, where

If  and
and  are chosen such that
are chosen such that  for some
for some  and
and  for some
for some 
 with
with  , then the sequence
, then the sequence  defined by the following manners:
defined by the following manners:

converges weakly to some element  of
of  , where
, where  is the
is the  -uniformly smoothness constant of
-uniformly smoothness constant of  .
.
In this paper, motivated by Aoyama et al. [6], Iiduka et al. [2], Takahahsi and Toyoda [4], we introduce an iterative method to approximate a solution of variational inequality (1.15) for an  -inverse strongly accretive operators. Strong convergence theorems are obtained in the framework of Banach spaces under appropriate conditions on parameters.
-inverse strongly accretive operators. Strong convergence theorems are obtained in the framework of Banach spaces under appropriate conditions on parameters.
We also need the following lemmas for proof of our main results.
Lemma 1.2 (see [7]).
Let  be a given real number with
be a given real number with  and let
and let  be a
be a  -uniformly smooth Banach space. Then
-uniformly smooth Banach space. Then

for all  , where
, where  is the
is the  -uniformly smoothness constant of
-uniformly smoothness constant of  .
.
The following lemma is characterized by the set of solutions of variational inequality (1.15) by using sunny nonexpansive retractions.
Lemma 1.3 (see [6]).
Let  be a nonempty closed convex subset of a smooth Banach space
be a nonempty closed convex subset of a smooth Banach space  . Let
. Let  be a sunny nonexpansive retraction from
be a sunny nonexpansive retraction from  onto
onto  and let
and let  be an accretive operator of
be an accretive operator of  into
into  . Then, for all
. Then, for all  ,
,

Lemma 1.4 (see [8]).
Let  be a nonempty bounded closed convex subset of a uniformly convex Banach space
be a nonempty bounded closed convex subset of a uniformly convex Banach space  and let
and let  be nonexpansive mapping of
be nonexpansive mapping of  into itself. If
into itself. If  is a sequence of
is a sequence of  such that
such that  weakly and
weakly and  , then
, then  is a fixed point of
is a fixed point of  .
.
Lemma 1.5 (see [9]).
Let  ,
,  be bounded sequences in a Banach space
be bounded sequences in a Banach space  and let
and let  be a sequence in
be a sequence in  which satisfies the following condition:
which satisfies the following condition:

Suppose that

for all  and
and

Then  .
.
Lemma 1.6 (see [10]).
Assume that  is a sequence of nonnegative real numbers such that
is a sequence of nonnegative real numbers such that

for all  , where
, where  is a sequence in
is a sequence in  and
and  is a sequence in
is a sequence in  such that
such that
(i) ;
;
(ii) or
or  .
.
Then  .
.
2. Main Results
Theorem 2.1.
Let  be a uniformly convex and
be a uniformly convex and  -uniformly smooth Banach space and
-uniformly smooth Banach space and  a nonempty closed convex subset of
a nonempty closed convex subset of  . Let
. Let  be a sunny nonexpansive retraction from
be a sunny nonexpansive retraction from  onto
onto  ,
,  an arbitrarily fixed point, and
an arbitrarily fixed point, and  an
an  -inverse strongly accretive operator of
-inverse strongly accretive operator of  into
into  such that
such that  . Let
. Let  and
and  be two sequences in
be two sequences in  and let
and let  a real number sequence in
a real number sequence in  for some
for some  satisfying the following conditions:
satisfying the following conditions:
(i) and
and  ;
;
(ii) ;
;
(iii) .
.
Then the sequence  defined by
defined by

converges strongly to  , where
, where  is a sunny nonexpansive retraction of
is a sunny nonexpansive retraction of  onto
onto  .
.
Proof.
First, we show that  is nonexpansive for all
is nonexpansive for all  . Indeed, for all
. Indeed, for all  and
and  , from Lemma 1.2, one has
, from Lemma 1.2, one has

Therefore, one obtains that  is a nonexpansive mapping for all
is a nonexpansive mapping for all  . For all
. For all  , it follows from Lemma 1.3 that
, it follows from Lemma 1.3 that  . Put
. Put  . Noticing that
. Noticing that

one has

from which it follows that

Now, an induction yields

Hence,  is bounded, and so is
is bounded, and so is  . On the other hand, one has
. On the other hand, one has

Put  , that is,
, that is,

Next, we compute  Observing that
Observing that

we have

Combining (2.7) with (2.10), one obtains

It follows that

Hence, from Lemma 1.5, we obtain  . From (2.7) and the condition (ii), one arrives at
. From (2.7) and the condition (ii), one arrives at

On the other hand, from (2.1), one has

which combines with (2.13), and from the conditions (i), (ii), one sees that

Next, we show that

To show (2.16), we choose a sequence  of
of  that converges weakly to
that converges weakly to  such that
such that

Next, we prove that  . Since
. Since  for some
for some  , it follows that
, it follows that  is bounded and so there exists a subsequence
is bounded and so there exists a subsequence  of
of  which converges to
which converges to  . We may assume, without loss of generality, that
. We may assume, without loss of generality, that  . Since
. Since  is nonexpansive, it follows from
is nonexpansive, it follows from  that
that

It follows from (2.15) that

From Lemma 1.4, we have  . It follows from Lemma 1.3 that
. It follows from Lemma 1.3 that  . Now, from (2.17) and Lemma 1.1, we have
. Now, from (2.17) and Lemma 1.1, we have

From (2.1), we have

It follows that

Applying Lemma 1.6 to (2.22), we can conclude the desired conclusion. This completes the proof.
As an application of Theorem 2.1, we have the following results in the framework of Hilbert spaces.
Corollary 2.2.
Let  be a Hilbert space and
be a Hilbert space and  a nonempty closed convex subset of
a nonempty closed convex subset of  . Let
. Let  be a metric projection from
be a metric projection from  onto
onto  ,
,  an arbitrarily fixed point, and
an arbitrarily fixed point, and  an
an  -inverse strongly monotone operator of
-inverse strongly monotone operator of  into
into  such that
such that  . Let
. Let  and
and  be two sequences in
be two sequences in  and let
and let  be a real number sequence in
be a real number sequence in  for some
for some  satisfying the following conditions:
satisfying the following conditions:
(i) and
and  ;
;
(ii) ;
;
(iii) .
.
Then the sequence  defined by
defined by

converges strongly to  .
.
References
Browder FE, Petryshyn WV: Construction of fixed points of nonlinear mappings in Hilbert space. Journal of Mathematical Analysis and Applications 1967,20(2):197–228. 10.1016/0022-247X(67)90085-6
Iiduka H, Takahashi W, Toyoda M: Approximation of solutions of variational inequalities for monotone mappings. PanAmerican Mathematical Journal 2004,14(2):49–61.
Kamimura S, Takahashi W: Weak and strong convergence of solutions to accretive operator inclusions and applications. Set-Valued Analysis 2000,8(4):361–374. 10.1023/A:1026592623460
Takahashi W, Toyoda M: Weak convergence theorems for nonexpansive mappings and monotone mappings. Journal of Optimization Theory and Applications 2003,118(2):417–428. 10.1023/A:1025407607560
Xu H-K: Viscosity approximation methods for nonexpansive mappings. Journal of Mathematical Analysis and Applications 2004,298(1):279–291. 10.1016/j.jmaa.2004.04.059
Aoyama K, Iiduka H, Takahashi W: Weak convergence of an iterative sequence for accretive operators in Banach spaces. Fixed Point Theory and Applications 2006, 2006:-13.
Xu H-K: Inequalities in Banach spaces with applications. Nonlinear Analysis: Theory, Methods & Applications 1991,16(12):1127–1138. 10.1016/0362-546X(91)90200-K
Browder FE: Nonlinear operators and nonlinear equations of evolution in Banach spaces. In Nonlinear Functional Analysis (Proceedings of Symposia in Pure Mathematics, Vol. 18, Part 2, Chicago, Ill., 1968). American Mathematical Society, Providence, RI, USA; 1976:1–308.
Suzuki T: Strong convergence of Krasnoselskii and Mann's type sequences for one-parameter nonexpansive semigroups without Bochner integrals. Journal of Mathematical Analysis and Applications 2005,305(1):227–239. 10.1016/j.jmaa.2004.11.017
Xu HK: An iterative approach to quadratic optimization. Journal of Optimization Theory and Applications 2003,116(3):659–678. 10.1023/A:1023073621589
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hao, Y. Strong Convergence of an Iterative Method for Inverse Strongly Accretive Operators. J Inequal Appl 2008, 420989 (2008). https://doi.org/10.1155/2008/420989
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/420989
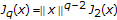
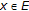 with
with 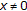 ;
;
 and
and 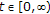 ;
;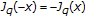
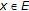 .
.
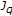 is single-valued and uniformly continuous on any bounded subset of
is single-valued and uniformly continuous on any bounded subset of  ;
;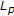 (or
(or  ) spaces (
) spaces (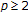 ), and the Sobolev spaces,
), and the Sobolev spaces,  (
(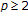 ), are
), are  -uniformly smooth, while
-uniformly smooth, while 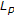 (or
(or 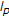 ) and
) and 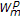 spaces (
spaces (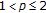 ) are
) are  -uniformly smooth.
-uniformly smooth.