- Research Article
- Open access
- Published:
Strict Stability Criteria for Impulsive Functional Differential Systems
Journal of Inequalities and Applications volume 2008, Article number: 243863 (2007)
Abstract
By using Lyapunov functions and Razumikhin techniques, the strict stability of impulsive functional differential systems is investigated. Some comparison theorems are given by virtue of differential inequalities. The corresponding theorems in the literature can be deduced from our results.
1. Introduction
Since time-delay systems are frequently encountered in engineering, biology, economy, and other disciplines, it is significant to study these systems [1]. On the other hand, because many evolution processes in nature are characterized by the fact that at certain moments of time they experience an abrupt change of state, the study of dynamic systems with impulse effects has been assuming greater importance [2–4]. It is natural to expect that the hybrid systems which are called impulsive functional differential systems can represent a truer framework for mathematical modeling of many real world phenomena. Recently, several papers dealing with stability problem for impulsive functional differential systems have been published [5–10].
The usual stability concepts do not give any information about the rate of decay of the solutions, and hence are not strict concepts. Consequently, strict-stability concepts have been defined and criteria for such notions to hold are discussed in [11]. Till now, to the best of our knowledge, only the following very little work has been done in this direction [12–15].
In this paper, we investigate strict stability for impulsive functional differential systems. The paper is organized as follows. In Section 2, we introduce some basic definitions and notations. In Section 3, we first give two comparison lemmas on differential inequalities. Then, by these lemmas, a comparison theorem is obtained and several direct results are deduced from it. An example is also given to illustrate the advantages of our results.
2. Preliminaries
We consider the following impulsive functional differential system:

where  is the set of all positive integers,
is the set of all positive integers,  ,
,  is an open set in
is an open set in 

 , here
, here  , and
, and  is continuous everywhere except for a finite number of points
is continuous everywhere except for a finite number of points  at which
at which  and
and  exist and
exist and  .
.  for each
for each  , where
, where  denotes the norm of vector in
denotes the norm of vector in  ,
,  with
with  as
as  and
and  denotes the right-hand derivative of
denotes the right-hand derivative of  . For each
. For each  ,
,  is defined by
is defined by  ,
,  . For
. For  ,
, 
 ,
,  . We assume that
. We assume that  and
and  , so that
, so that  is a solution of (2.1), which we call the zero solution.
is a solution of (2.1), which we call the zero solution.
Let  for some
for some  and
and  , a function
, a function 
 is said to be a solution of (2.1) with the initial condition
is said to be a solution of (2.1) with the initial condition

if it is continuous and satisfies the differential equation  in each
in each 
 , and at
, and at  it satisfies
it satisfies  .
.
Throughout this paper, we always assume the following conditions hold to ensure the global existence and uniqueness of solution of (2.1) through  .
.
(H1) is continuous on
is continuous on  for each
for each  and for all
and for all  and
and  , the limits
, the limits  exist.
exist.
(H2) is Lipschitzian in
is Lipschitzian in  in each compact set in
in each compact set in  .
.
(H3) for all
for all  and there exists
and there exists  such that
such that  implies that
implies that  for all
for all  .
.
The function  belongs to class
belongs to class  if the following hold.
if the following hold.
(A1) is continuous on each of the sets
is continuous on each of the sets  and for each
and for each  and
and  ,
,  exists.
exists.
(A2) is locally Lipschitzian in
is locally Lipschitzian in  and for
and for  Let
Let  ,
,  along the solution
along the solution  of (2.1) is defined as
of (2.1) is defined as

Let us introduce the following notations for further use:
(i)
(ii)

(iii)
(iv) ;
;
(v) ;
;
(vi) .
.
Definition 2.1.
The zero solution of (2.1) is said to be strictly stable (SS), if for any  and
and  , there exists a
, there exists a  such that
such that  implies
implies  for
for  and for every
and for every  , there exists an
, there exists an  such that
such that

Definition 2.2.
The zero solution of (2.1) is said to be strictly uniformly stable (SUS), if  , and
, and  in (SS) are independent of
in (SS) are independent of  .
.
Remark 2.3.
If in (SS) or (SUS),  , we obtain nonstrict stabilities, that is, the usual stability or uniform stability, respectively. Moreover, strict stability immediately implies that the zero solution is not asymptotically stable.
, we obtain nonstrict stabilities, that is, the usual stability or uniform stability, respectively. Moreover, strict stability immediately implies that the zero solution is not asymptotically stable.
The preceding notions imply that the motion remains in the tube like domains. To obtain sufficient conditions for such stability concepts to hold, it is necessary to simultaneously obtain both lower and upper bounds of the derivative of Lyapunov function. Thus, we need to consider the following two auxiliary systems:

and

where  ,
,  ,
, 


 for each
for each  .
.
From the theory of impulsive differential systems [2], we obtain that

where  and
and  are the minimal and maximal solutions of (2.5), (2.6), respectively.
are the minimal and maximal solutions of (2.5), (2.6), respectively.
The corresponding definitions of strict stability of the auxiliary systems (2.5), (2.6) are as follows.
Definition 2.4.
The zero solutions of comparison systems (2.5), (2.6), as a system, are said to be strictly stable (SS*), if for any  and
and  , there exist a
, there exist a  and
and  satisfying
satisfying  such that
such that

Definition 2.5.
The zero solutions of comparison systems (2.5),(2.6), as a system , are said to be strictly uniformly stable (SUS*), if  , and
, and  in (SS*) are independent of
in (SS*) are independent of  .
.
3. Main Results
We first give two Razumikhin-type comparison lemmas on differential inequalities.
Lemma 3.1.
Assume that
(i) for each
for each  ;
;
(ii)there exists  , where
, where  are continuous on
are continuous on  and
and  exist,
exist,  , satisfying
, satisfying

Then


where  and
and  are the minimal and maximal solutions of systems (3.4) and (3.5), respectively,
are the minimal and maximal solutions of systems (3.4) and (3.5), respectively,


Proof.
First, we prove that (3.2) holds. Otherwise, there exist  such that
such that
(a) ,
,
(b) and
and
(c) .
.
By (a), (b), and (ii), applying the classical comparison theorem, we have

which contradicts (c). So (3.2) is correct. Equation (3.3) can be proved in the same way as above. Then Lemma 3.1 holds.
Lemma 3.2.
Assume that (i) in Lemma 3.1 holds. Suppose further that
-
(ii)
there exists
 satisfying
satisfying 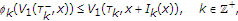 (3.7)
(3.7)
where  and for any solution
and for any solution  of (2.1),
of (2.1), 
 implies that
implies that

-
(iii)
there exists
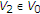 satisfying
satisfying 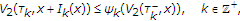 (3.9)
(3.9)
where  , and for any solution
, and for any solution  of (2.1),
of (2.1), 
 implies that
implies that

Then


where  and
and  are the minimal and maximal solutions of (2.5), (2.6), respectively.
are the minimal and maximal solutions of (2.5), (2.6), respectively.
Proof.
Assume  . First, we prove that (3.11) holds for
. First, we prove that (3.11) holds for  , that is
, that is

Let  . Equation (3.13) holds obviously by Lemma 3.1 for
. Equation (3.13) holds obviously by Lemma 3.1 for  . By (ii),
. By (ii),  . The same proof as for
. The same proof as for  leads to
leads to

By induction, (3.11) is correct. Similarly, (3.12) can be proved by using Lemma 3.1 and assumption (iii).
Using Lemma 3.2, we can easily get the following theorem about strict stability properties of (2.1).
Theorem 3.3.
Assume that all the conditions of Lemma 3.2 hold. Suppose further that there exist functions  , such that
, such that
-
(iv)
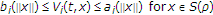
.
Then the strict stability properties of comparison systems (2.5), (2.6) imply the corresponding strict stability properties of zero solution of (2.1).
Proof.
First, let us prove strict stability of the zero solution of (2.1). Suppose that  and
and  are given. Assume that (SS*) holds. Then, given
are given. Assume that (SS*) holds. Then, given  , there exists
, there exists  , and
, and  satisfying
satisfying  such that
such that

By (iv), there exist  such that for
such that for  ,
,

Next, choose  such that
such that  and
and  . We claim that with the choices of
. We claim that with the choices of  , and
, and  , the zero solution of (2.1) is strictly stable. That means that if
, the zero solution of (2.1) is strictly stable. That means that if  is any solution of (2.1),
is any solution of (2.1),  implies that
implies that  . If not, we have either of the following alternatives.
. If not, we have either of the following alternatives.
Case 1.
There exists a  such that
such that

Then clearly  . Thus, by Lemma 3.2, (i) and (ii) imply that
. Thus, by Lemma 3.2, (i) and (ii) imply that

Using (3.15)–(3.18) and (iv), we get

which is a contradiction.
Case 2.
There exists a  such that
such that


By (H3), (3.21) yields

Because of (3.20) and (3.22), there exists a  such that
such that

By Lemma 3.2, (i) and (iii) imply that

From (3.15), (3.23), (3.24), and (iv), we have the following contradiction:

We, therefore, obtain the strict stability of the zero solution of (2.1). If we assume that the zero solutions of comparison systems (2.5), (2.6) are (SUS*), since  are independent of
are independent of  , we obtain, because of (iv),
, we obtain, because of (iv),  and
and  in (3.16) are independent of
in (3.16) are independent of  , and hence, (SUS) of (2.1) holds.
, and hence, (SUS) of (2.1) holds.
Using Theorem 3.3, we can get two direct results on strictly uniform stability of zero solution of (2.1) and the first one is Theorem 3.3 in [15].
Corollary 3.4.
In Theorem 3.3, suppose that 
 , where
, where  , and
, and 
 .
.
Then the zero solution of (2.1) is strictly uniformly stable.
Corollary 3.5.
In Theorem 3.3, suppose that  , where
, where  and
and  are bounded,
are bounded,  and
and  are just the same as in Corollary 3.4.
are just the same as in Corollary 3.4.
Then the zero solution of (2.1) is strictly uniformly stable.
Proof.
Under the given hypotheses, it is easy to obtain the solutions of (2.5) and (2.6):

Since  are bounded, there exist two positive constants
are bounded, there exist two positive constants  such that
such that  . Also, since
. Also, since  , it follows that
, it follows that 
 and
and  , obviously
, obviously  . Given
. Given  choose
choose  and for
and for  , choose
, choose  . Then, if
. Then, if  , we have
, we have

That is, the zero solutions of (2.5), (2.6) are strictly uniformly stable. Hence, by Theorem 3.3, the zero solution of (2.1) is strictly uniformly stable.
Example 3.6.
Consider the system

where  are continuous on
are continuous on  . Assume that
. Assume that 
 with
with 
 , and
, and  .
.
Let  , then
, then

For any solution  of (3.28) such that
of (3.28) such that  we have
we have

and if  , we have
, we have

By Corollary 3.5, the zero solution of (2.1) is strictly uniformly stable.
References
Hale J: Theory of Functional Differential Equations, Applied Mathematical Sciences. Volume 3. 2nd edition. Springer, New York, NY, USA; 1977:x+365.
Lakshmikantham V, Baĭnov DD, Simeonov PS: Theory of Impulsive Differential Equations, Series in Modern Applied Mathematics. Volume 6. World Scientific, Teaneck, NJ, USA; 1989:xii+273.
Fu XL, Yan BQ, Liu YS: Introduction to Impulsive Differential Systems. Science Press, Beijing, China; 2005.
Fu XL, Wang KN, Lao HX: Boundedness of perturbed systems with impulsive effects. Acta Mathematica Scientia. Series A 2004,24(2):135–143.
Shen J, Yan J: Razumikhin type stability theorems for impulsive functional-differential equations. Nonlinear Analysis: Theory, Methods & Applications 1998,33(5):519–531. 10.1016/S0362-546X(97)00565-8
Shen JH: Razumikhin techniques in impulsive functional-differential equations. Nonlinear Analysis: Theory, Methods & Applications 1999,36(1):119–130. 10.1016/S0362-546X(98)00018-2
Yan J, Shen J: Impulsive stabilization of functional-differential equations by Lyapunov-Razumikhin functions. Nonlinear Analysis: Theory, Methods & Applications 1999,37(2):245–255. 10.1016/S0362-546X(98)00045-5
Luo Z, Shen J: New Razumikhin type theorems for impulsive functional differential equations. Applied Mathematics and Computation 2002,125(2–3):375–386.
Xing Y, Han M: A new approach to stability of impulsive functional differential equations. Applied Mathematics and Computation 2004,151(3):835–847. 10.1016/S0096-3003(03)00540-X
Liu K, Fu X: Stability of functional differential equations with impulses. Journal of Mathematical Analysis and Applications 2007,328(2):830–841. 10.1016/j.jmaa.2006.05.071
Lakshmikantham V, Leela S: Differential and Integral Inequalities: Theory and Applications. Vol. I: Ordinary Differential Equations, Mathematics in Science and Engineering. Volume 55. Academic Press, New York; 1969:ix+390.
Lakshmikantham V, Vasundhara Devi J: Strict stability criteria for impulsive differential systems. Nonlinear Analysis: Theory, Methods & Applications 1993,21(10):785–794. 10.1016/0362-546X(93)90123-A
Lakshmikantham V, Zhang Y: Strict practical stability of delay differential equation. Applied Mathematics and Computation 2001,122(3):341–351. 10.1016/S0096-3003(00)00049-7
Lakshmikantham V, Mohapatra RN: Strict stability of differential equations. Nonlinear Analysis: Theory, Methods & Applications 2001,46(7):915–921. 10.1016/S0362-546X(00)00122-X
Zhang Y, Sun J: Strict stability of impulsive functional differential equations. Journal of Mathematical Analysis and Applications 2005,301(1):237–248. 10.1016/j.jmaa.2004.07.018
Acknowledgments
This project is supported by the National Natural Science Foundation of China (60673101) and the Natural Science Foundation of Shandong Province (Y2007G30). The authors are grateful to the referees for their helful comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Liu, K., Yang, G. Strict Stability Criteria for Impulsive Functional Differential Systems. J Inequal Appl 2008, 243863 (2007). https://doi.org/10.1155/2008/243863
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/243863
 satisfying
satisfying 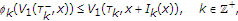
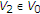 satisfying
satisfying