- Research Article
- Open access
- Published:
On the -Boundedness of Nonisotropic Spherical Riesz Potentials
-Boundedness of Nonisotropic Spherical Riesz Potentials
Journal of Inequalities and Applications volume 2007, Article number: 036503 (2007)
Abstract
We introduced the concept of nonisotropic spherical Riesz potential operators generated by the -distance of variable order on
-distance of variable order on -sphere and its
-sphere and its -boundedness were investigated.
-boundedness were investigated.
References
Besov OV, Il'in VP, Lizorkin PI: The
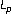 -estimates of a certain class of non-isotropically singular integrals. Doklady Akademii Nauk SSSR 1966, 169: 1250–1253.
-estimates of a certain class of non-isotropically singular integrals. Doklady Akademii Nauk SSSR 1966, 169: 1250–1253.Çınar İ: The Hardy-Littlewood-Sobolev inequality for non-isotropic Riesz potentials. Turkish Journal of Mathematics 1997,21(2):153–157.
Çınar İ, Duru H: The Hardy-Littlewood-Sobolev inequality for
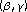 -distance Riesz potentials. Applied Mathematics and Computation 2004,153(3):757–762. 10.1016/S0096-3003(03)00671-4
-distance Riesz potentials. Applied Mathematics and Computation 2004,153(3):757–762. 10.1016/S0096-3003(03)00671-4Gadjiev AD, Dogru O: On combination of Riesz potentials with non-isotropic kernels. Indian Journal of Pure and Applied Mathematics 1999,30(6):545–556.
Sarikaya MZ, Yıldırım H: The restriction and the continuity properties of potentials depending on
 -distance. Turkish Journal of Mathematics 2006,30(3):263–275.
-distance. Turkish Journal of Mathematics 2006,30(3):263–275.Sarikaya MZ, Yıldırım H: On the
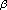 -spherical Riesz potential generated by the
-spherical Riesz potential generated by the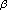 -distance. International Journal of Contemporary Mathematical Sciences 2006,1(2):85–89.
-distance. International Journal of Contemporary Mathematical Sciences 2006,1(2):85–89.Sarikaya MZ, Yıldırım H: On the non-isotropic fractional integrals generated by the
 -distance. Selçuk Journal of Applied Mathematics 2006,7(1):17–23.
-distance. Selçuk Journal of Applied Mathematics 2006,7(1):17–23.Sarikaya MZ, Yıldırım H: On the Hardy type inequality with non-isotropic kernels. Lobachevskii Journal of Mathematics 2006, 22: 47–57.
Sarikaya MZ, Yıldırım H, Ozkan UM: Norm inequalities with non-isotropic kernels. International Journal of Pure and Applied Mathematics 2006,31(3):337–344.
Stein EM: Singular Integrals and Differentiability Properties of Functions, Princeton Mathematical Series, no. 30. Princeton University Press, Princeton, NJ, USA; 1970:xiv+290.
Zhou Z, Hong Y, Zhou CZ: The-boundedness of Riesz potential operators of variable order on a sphere. Journal of South China Normal University 1999, (2):20–24.
Yıldırım H: On generalization of the quasi homogeneous Riesz potential. Turkish Journal of Mathematics 2005,29(4):381–387.
Sadosky C: Interpolation of Operators and Singular Integrals, Monographs and Textbooks in Pure and Applied Math.. Volume 53. Marcel Dekker, New York, NY, USA; 1979:xii+375.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sarikaya, M., Yildirim, H. On the -Boundedness of Nonisotropic Spherical Riesz Potentials.
J Inequal Appl 2007, 036503 (2007). https://doi.org/10.1155/2007/36503
-Boundedness of Nonisotropic Spherical Riesz Potentials.
J Inequal Appl 2007, 036503 (2007). https://doi.org/10.1155/2007/36503
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/36503
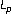 -estimates of a certain class of non-isotropically singular integrals. Doklady Akademii Nauk SSSR 1966, 169: 1250–1253.
-estimates of a certain class of non-isotropically singular integrals. Doklady Akademii Nauk SSSR 1966, 169: 1250–1253.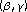 -distance Riesz potentials. Applied Mathematics and Computation 2004,153(3):757–762. 10.1016/S0096-3003(03)00671-4
-distance Riesz potentials. Applied Mathematics and Computation 2004,153(3):757–762. 10.1016/S0096-3003(03)00671-4 -distance. Turkish Journal of Mathematics 2006,30(3):263–275.
-distance. Turkish Journal of Mathematics 2006,30(3):263–275.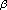 -spherical Riesz potential generated by the
-spherical Riesz potential generated by the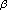 -distance. International Journal of Contemporary Mathematical Sciences 2006,1(2):85–89.
-distance. International Journal of Contemporary Mathematical Sciences 2006,1(2):85–89. -distance. Selçuk Journal of Applied Mathematics 2006,7(1):17–23.
-distance. Selçuk Journal of Applied Mathematics 2006,7(1):17–23.