- Research Article
- Open access
- Published:
A Multidimensional Functional Equation Having Quadratic Forms as Solutions
Journal of Inequalities and Applications volume 2007, Article number: 024716 (2007)
Abstract
We obtain the general solution and the stability of the -variable quadratic functional equation
-variable quadratic functional equation The quadratic form
The quadratic form is a solution of the given functional equation.
is a solution of the given functional equation.
References
Aczél J, Dhombres J: Functional Equations in Several Variables, Encyclopedia of Mathematics and Its Applications. Volume 31. Cambridge University Press, Cambridge, UK; 1989:xiv+462.
Bae J-H, Jun K-W: On the generalized Hyers-Ulam-Rassias stability of an
 -dimensional quadratic functional equation. Journal of Mathematical Analysis and Applications 2001,258(1):183–193. 10.1006/jmaa.2000.7372
-dimensional quadratic functional equation. Journal of Mathematical Analysis and Applications 2001,258(1):183–193. 10.1006/jmaa.2000.7372Bae J-H, Park W-G: On the generalized Hyers-Ulam-Rassias stability in Banach modules over a
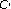 -algebra. Journal of Mathematical Analysis and Applications 2004,294(1):196–205. 10.1016/j.jmaa.2004.02.009
-algebra. Journal of Mathematical Analysis and Applications 2004,294(1):196–205. 10.1016/j.jmaa.2004.02.009Bae J-H, Park W-G: On stability of a functional equation with
 -variables. Nonlinear Analysis: Theory, Methods & Applications 2006,64(4):856–868. 10.1016/j.na.2005.06.028
-variables. Nonlinear Analysis: Theory, Methods & Applications 2006,64(4):856–868. 10.1016/j.na.2005.06.028Jung S-M: On the Hyers-Ulam stability of the functional equations that have the quadratic property. Journal of Mathematical Analysis and Applications 1998,222(1):126–137. 10.1006/jmaa.1998.5916
Park W-G, Bae J-H: On a bi-quadratic functional equation and its stability. Nonlinear Analysis: Theory, Methods & Applications 2005,62(4):643–654. 10.1016/j.na.2005.03.075
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Park, WG., Bae, JH. A Multidimensional Functional Equation Having Quadratic Forms as Solutions. J Inequal Appl 2007, 024716 (2007). https://doi.org/10.1155/2007/24716
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/24716
 -dimensional quadratic functional equation. Journal of Mathematical Analysis and Applications 2001,258(1):183–193. 10.1006/jmaa.2000.7372
-dimensional quadratic functional equation. Journal of Mathematical Analysis and Applications 2001,258(1):183–193. 10.1006/jmaa.2000.7372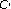 -algebra. Journal of Mathematical Analysis and Applications 2004,294(1):196–205. 10.1016/j.jmaa.2004.02.009
-algebra. Journal of Mathematical Analysis and Applications 2004,294(1):196–205. 10.1016/j.jmaa.2004.02.009 -variables. Nonlinear Analysis: Theory, Methods & Applications 2006,64(4):856–868. 10.1016/j.na.2005.06.028
-variables. Nonlinear Analysis: Theory, Methods & Applications 2006,64(4):856–868. 10.1016/j.na.2005.06.028